Сумма геометрической прогрессии бесконечной убывающей и сумма ее квадратов

Геометрическая прогрессия представляет собой один из самых интересных числовых рядов, которые рассматривают в школьном курсе алгебры. Данная статья посвящена частному случаю упомянутого ряда: убывающей бесконечной геометрической прогрессии и сумме ее членов.

О каком ряде чисел пойдет речь?

Прогрессией геометрической называют одномерную последовательность действительных чисел, которые связаны друг с другом следующим соотношением:

a₂ = a₁*r, a₃ = a₂*r, a₄ = a₃*r, ...., a_n = a_n-1*r

Обобщая выражения выше, можно записать следующее равенство:

a_n = a₁*r^n-1

Как понятно из приведенных записей, a_n - это элемент прогрессии с номером n. Параметр r, на который следует умножить n-1 элемент, чтобы получить n-й, называют знаменателем.

Какими свойствами обладает описанная последовательность? Ответ на вопрос зависит от величины и знака r. Возможны следующие варианты:

• Знаменатель r положительный и больше 1. Прогрессия в этом случае всегда будет возрастать по модулю, при этом абсолютное значение ее членов может и убывать, если a₁ будет отрицательным.
• Знаменатель r отрицательный и больше 1. В таком случае члены прогрессии будут появляться с чередованием знака (+ и -). Подобные ряды мало интересны для практики.
• Модуль знаменателя r меньше 1. Этот ряд называется убывающим, причем независимо от знака r. Именно эта прогрессия представляет большой практический интерес, о ней пойдет речь в данной статье.

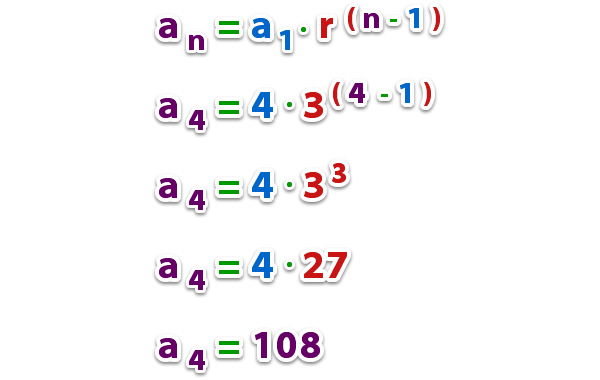
Формула для суммы

Получим для начала выражение, которое позволит вычислить сумму произвольного количества элементов заданной прогрессии. Начнем решать эту задачу в лоб. Имеем:

S_n = a₁+a₂+a₃+..+a_n

Приведенным равенством можно пользоваться, если необходимо посчитать результат для небольшого числа членов (3-4 слагаемых), каждый из которых определяется по формуле для n-го члена (см. предыдущий пункт). Однако если слагаемых становится много, то в лоб считать неудобно и можно допустить ошибку, поэтому пользуются специальной формулой.

Обе части равенства выше умножим на r, получаем:

r*S_n = r*a₁+r*a₂+r*a₃+..+r*a_n = a₂+a₃+a₄+...+a_n+1

Теперь попарно вычтем левые и правые части этих двух выражений, имеем:

r*S_n - S_n = a₂+a₃+a₄+...+a_n+1 - (a₁+a₂+a₃+..+a_n) = a_n+1 - a₁

Выражая сумму S_n и пользуясь формулой для члена a_n+1, получим:

S_n = (a_n+1 - a₁)/(r-1) = a₁*(rⁿ - 1)/(r-1)

Таким образом, мы получили общую формулу для суммы первых n слагаемых рассматриваемого типа числового ряда. Заметим, что формула справедлива, если r≠1. В последнем случае имеет место простой ряд одинаковых чисел, сумма которых вычисляется как произведение одного числа на их количество.

Как находить сумму бесконечной геометрической прогрессии убывающей?

Чтобы ответить на этот вопрос, следует напомнить, что ряд будет убывающим, когда |r|<1. Воспользуемся полученной в предыдущем пункте формулой для S_n:

S_n = a₁*(rⁿ - 1)/(r-1)

Заметим, что любое число, модуль которого меньше 1, при возведении в большие степени стремится к нулю, то есть r^∞->0. Проверить этот факт можно на любом примере:

r = -1/2, тогда (-1/2)**10 ≈ 9,7*10^-4, (-1/2)**20 ≈ 9,5*10^-7 и так далее.

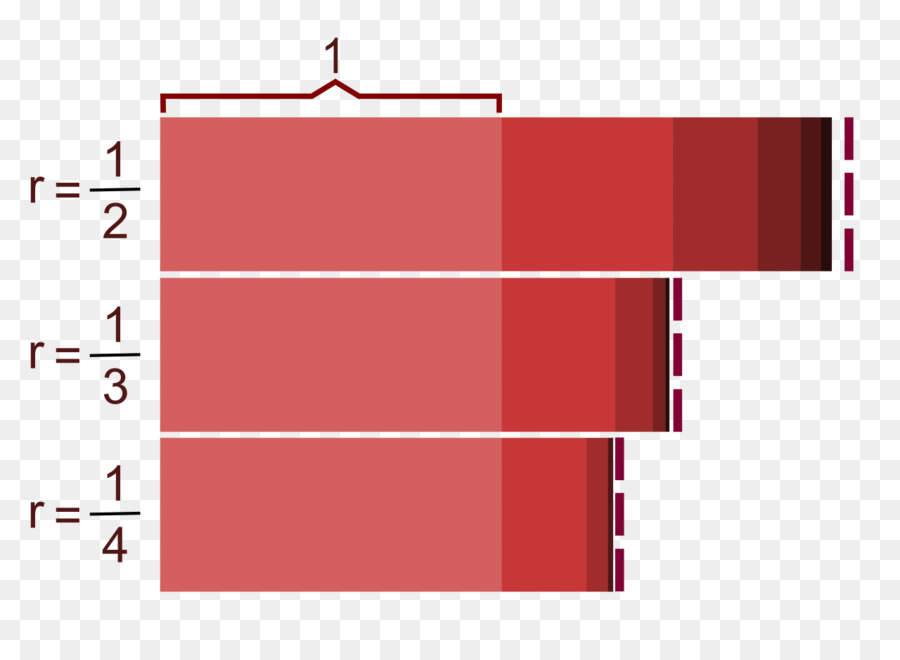
Установив этот факт, обратим внимание на выражение для суммы: при n->∞ оно будет переписано следующим образом:

S_∞ = a₁*(r^∞ - 1)/(r-1) = a₁/(1-r)

Получился интересный результат: сумма бесконечной прогрессии геометрической убывающей стремится к конечному числу, которое не зависит от количества слагаемых. Она определяется лишь первым членом и знаменателем. Заметим, что знак суммы однозначно определяется знаком a₁, поскольку знаменатель всегда является положительным числом (1-r>0).

Сумма квадратов бесконечной геометрической прогрессии убывающей

Название пункта определяет задачу, которую следует решить. Для этого воспользуемся методикой, которая полностью аналогична той, что применялась для вывода общей формулы для S_n. Имеем первое выражение:

M_n = a₁² + a₂² + a₃² + ... + a_n²

Умножим обе части равенства на r², записываем второе выражение:

r²*M_n = r²*a₁² + r²*a₂² + r²*a₃² + ... + r²*a_n² = a₂² + a₃² + a₄² ... + a_n+1²

Теперь находим разность этих двух равенств:

r²*M_n - M_n = a₂² + a₃² + a₄² ... + a_n+1² - (a₁² + a₂² + a₃² + ... + a_n²) = a_n+1² - a₁²

Выражаем M_n и используем формулу для n-го элемента, получаем равенство:

M_n = (a_n+1² - a₁²)/(r²-1)=a₁²*(r²ⁿ-1)/(r²-1)

В предыдущем пункте было показано, что r^∞ -> 0, тогда конечная формула примет вид:

M_∞ = a₁²*/(1-r²)

Сравнение двух полученных сумм

Сравним две формулы: для бесконечной суммы и бесконечной суммы квадратов на примере следующей задачи: сумма бесконечной геометрической прогрессии равна 2, известно, что речь идет об убывающей последовательности, для которой знаменатель равен 1/3. Необходимо найти бесконечную сумму квадратов этого ряда чисел.

Воспользуемся формулой для суммы. Выразим a₁:

S_∞ = a₁/(1-r) => a₁ = S_∞*(1-r)

Подставляем это выражение в формулу для суммы квадратов, имеем:

M_∞ = a₁²*/(1-r²) = S_∞²*(1-r)²/(1-r²) = S_∞²*(1-r)/(1+r)

Мы получили искомую формулу, теперь можно подставлять известные из условия данные:

M_∞ = S_∞²*(1-r)/(1+r) = 2²*(1-1/3)/(1+1/3) = 2

Таким образом, мы получили для бесконечной суммы квадратов такое же значение, что и для простой суммы. Заметим, что этот результат справедлив только для этой задачи. В общем случае M_∞ ≠ S_∞.

Задача на вычисление площади прямоугольника

Каждому школьнику известна формула S = a * b, которая определяет площадь прямоугольника через его стороны. Мало кто знает, что задачу нахождения площади этой фигуры можно легко решить, если воспользоваться суммой бесконечной геометрической прогрессии. Покажем, как это делается.

Разделим мысленно прямоугольник пополам. Площадь одной половинки примем за единицу. Теперь поделим вторую половинку еще пополам. Получим две половинки, одну из которых поделим еще пополам. Эту процедуру будем продолжать до бесконечности (см. рисунок ниже).

В итоге площадь прямоугольника в выбранных нами единицах будет равна:

S_∞ = 1+1/2+1/4+1/8+...

Видно, что эти слагаемые являются элементами убывающего ряда, у которого a₁ = 1 и r = 1/2. Воспользовавшись формулой для бесконечной суммы, получим:

S_∞ = 1 /(1-1/2) = 2

В выбранном нами масштабе половинка прямоугольника (одна единица) соответствует площади a*b/2. Это означает, что площадь всего прямоугольника равна:

S_∞ = 2*a*b/2 = a*b

Полученный результат является очевидным, тем не менее он показал, как можно применять убывающую прогрессию для решения задач в геометрии.