Как найти проекцию точки на плоскость: методика определения и пример решения задачи

При решении геометрических задач в пространстве часто возникает проблема определения расстояния между плоскостью и точкой. В некоторых случаях это необходимо для комплексного решения. Эту величину можно вычислить, если найти проекцию на плоскость точки. Рассмотрим этот вопрос подробнее в статье.

Уравнение для описания плоскости

Перед тем как перейти к рассмотрению вопроса касательно того, как найти проекцию точки на плоскость, следует познакомиться с видами уравнений, которые задают последнюю в трехмерном пространстве. Подробнее - ниже.

Уравнением общего вида, определяющим все точки, которые принадлежат данной плоскости, является следующее:

A*x + B*y + C*z + D = 0.

Первые три коэффициента - это координаты вектора, который называется направляющим для плоскости. Он совпадает с нормалью для нее, то есть является перпендикулярным. Этот вектор обозначают n¯(A; B; C). Свободный коэффициент D однозначно определяется из знания координат любой точки, принадлежащей плоскости.

Далее в статье будем использовать записанное уравнение. Оно требуется, чтобы найти проекцию точки на плоскость.

Понятие о проекции точки и ее вычисление

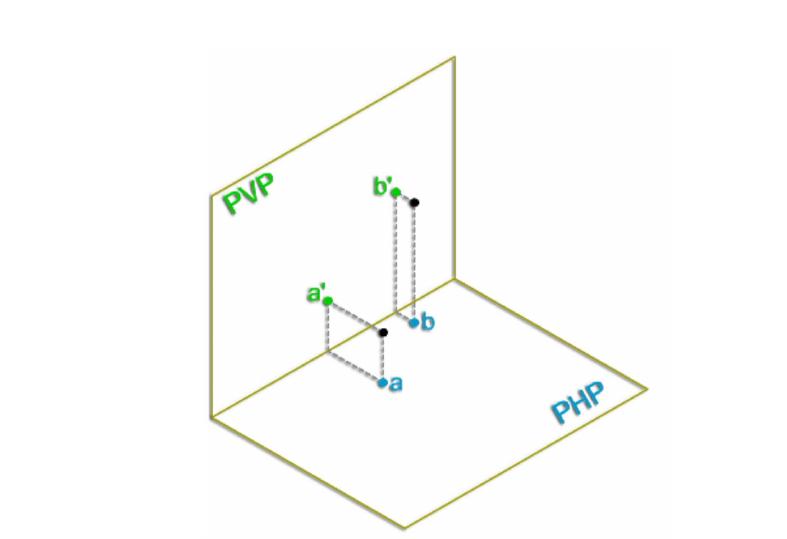
Предположим, что задана некоторая точка P(x₁; y₁; z₁) и плоскость. Она определена уравнением в общем виде. Если провести перпендикулярную прямую из P к заданной плоскости, то очевидно, что она пересечет последнюю в одной определенной точке Q (x₂; y₂; z₂). Q называется проекцией P на рассматриваемую плоскость. Длина отрезка PQ называется расстоянием от точки P до плоскости. Таким образом, сам PQ является перпендикулярным плоскости.

Как можно найти координаты проекции точки на плоскость? Сделать это не сложно. Для начала следует составить уравнение прямой, которая будет перпендикулярна плоскости. Ей будет принадлежать точка P. Поскольку вектор нормали n¯(A; B; C) этой прямой должен быть параллелен, то уравнение для нее в соответствующей форме запишется так:

(x; y; z) = (x₁; y₁; z₁) + λ*(A; B; C).

Где λ - действительное число, которое принято называть параметром уравнения. Изменяя его, можно получить любую точку прямой.

После того как записано векторное уравнение для перпендикулярной плоскости линии, необходимо найти общую точку пересечения для рассматриваемых геометрических объектов. Ее координаты и будут проекцией P. Поскольку они должны удовлетворять обоим равенствам (для прямой и для плоскости), то задача сводится к решению соответствующей системы линейных уравнений.

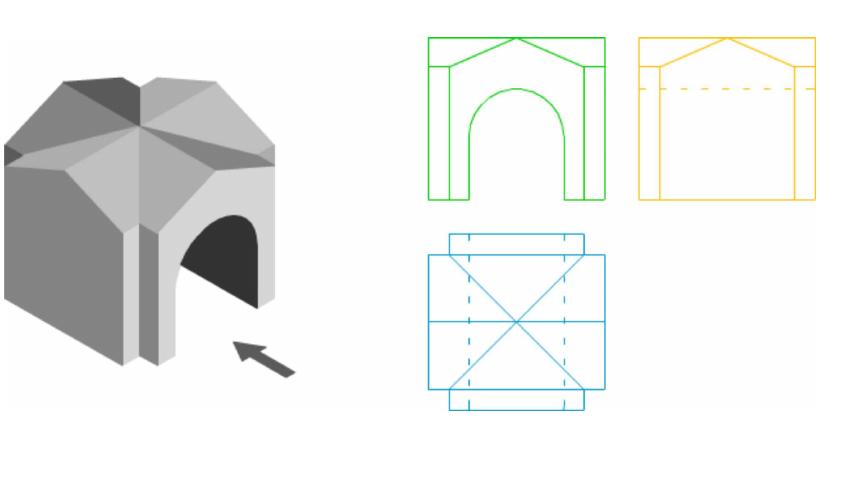
Понятие проекции часто используется при изучении чертежей. На них изображаются боковые и горизонтальные проекции детали на плоскости zy, zx, и xy.

Вычисление расстояния от плоскости до точки

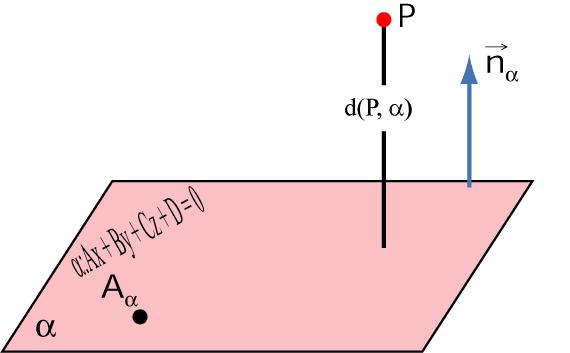
Как выше было отмечено, знание координат проекции на плоскость точки позволяет определить дистанцию между ними. Используя обозначения, введенные в предыдущем пункте, получаем, что искомое расстояние равно длине отрезка PQ. Для его вычисления достаточно найти координаты вектора PQ¯, а затем рассчитать его модуль по известной формуле. Конечное выражение для d расстояния между P точкой и плоскостью принимает вид:

d = |PQ¯| = √((x₂ - x₁)² + (y₂ - y₁)² + (z₂ - z₁)²).

Полученное значение d представлено в единицах, в которых задается текущая декартова координатная система xyz.

Пример задачи

Допустим, имеется точка N(0; -2; 3) и плоскость, которая описывается следующим уравнением:

2*x - y + z + 4 = 0.

Следует найти точки проекцию на плоскость и вычислить между ними расстояние.

В первую очередь составим уравнение прямой, которая пересекает плоскость под углом 90^o. Имеем:

(x; y; z) = (0; -2; 3) + λ*(2; -1; 1).

Записывая это равенство в явном виде, приходим к следующей системе уравнений:

x = 2*λ;

y = -2 - λ;

z = λ + 3;

2*x - y + z + 4 = 0.

Подставляя значения координат из первых трех равенств в четвертое, получим значение λ, определяющее координаты общей точки прямой и плоскости:

2*(2*λ) - (-2 - λ) + λ + 3 + 4 = 0 =>

6*λ + 9 = 0 =>

λ = 9/6 = 3/2 = 1,5.

Подставим найденный параметр в уравнение прямой и найдем координаты проекции исходной точки на плоскость:

(x; y; z) = (0; -2; 3) + 1,5*(2; -1; 1) = (3; -3,5; 4,5).

Для вычисления дистанции между заданными в условии задачи геометрическими объектами применим формулу для d:

d = √((3 - 0 )² + (-3,5 + 2 )² + (4,5 - 3 )²) = 3,674.

В данной задаче мы показали, как находить проекцию точки на произвольную плоскость и как вычислять между ними расстояние.