Существует такой забавный детский стишок, с помощью которого легко запомнить, что такое биссектриса: "Биссектриса - это такая крыса, что бегает по углам и делит угол пополам". Однако нельзя забывать, что, несмотря на простоту запоминания этого шуточного определения, учитель справедливо потребует другое, взятое из учебника.
В дальнейшем изучении школьной программы дети сталкиваются со сложной с первого взгляда задачей - как построить биссектрису данного угла с помощью циркуля. Однако уже более продвинутый школьник без труда справится с этим заданием, которое является основой выполнения цикла задач на построение в геометрии. Давайте же разберемся с этим вопросом раз и навсегда.
Как построить биссектрису данного угла?
Самым очевидным и наиболее простым способом является использование транспортира, но если данного вспомогательного инструмента не оказалось под рукой, надо уметь строить биссектрису без него.
Для выполнения данной задачи, как уже понял читатель, нам потребуется циркуль, а помимо него - линейка (важно понимать, что делениями на ней пользоваться нельзя) и простой карандаш с ластиком.
Алгоритм построения
Необходимо совершить такие действия:
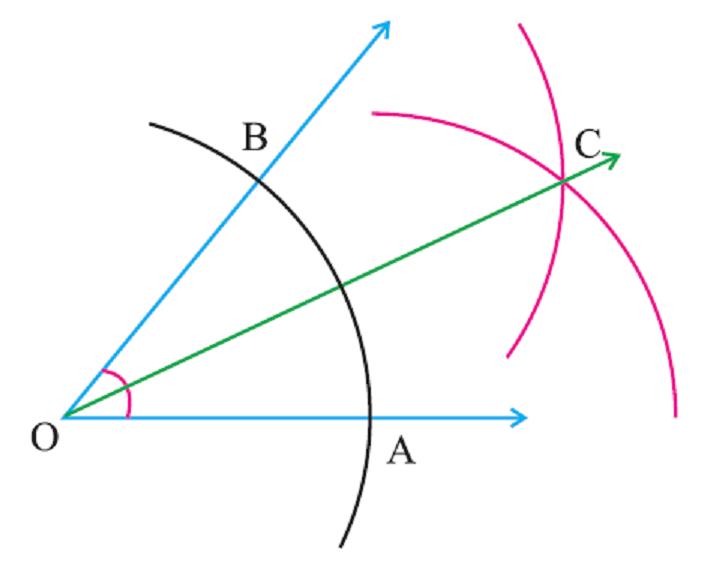
- Установите иглу циркуля в вершине данного угла.
- Установите циркулем произвольный радиус, проверните инструмент так, чтобы нарисованная им дуга пересекала оба луча, образующие угол.
- Отметьте точки пересечения дуги со сторонами заданного угла.
- Переставьте иглу циркуля в одну из отмеченных точек, выберете произвольный радиус и снова проверните циркуль таким образом, чтобы нарисованная им дуга была заключена внутри угла.
- Аналогичные действия проделайте, передвинув циркуль в точку, отмеченную на другой стороне угла. Важно сохранить радиус, выбранный в предыдущем пункте алгоритма.
- Отметьте точку пересечения двух дуг, которые были начерчены в двух предыдущих пунктах.
- Проведите луч из вершины угла, проходящий через эту точку.
- Полученный луч является искомым.
Мы дали ответ на поставленный вопрос - как построить биссектрису данного угла.
Доказательство
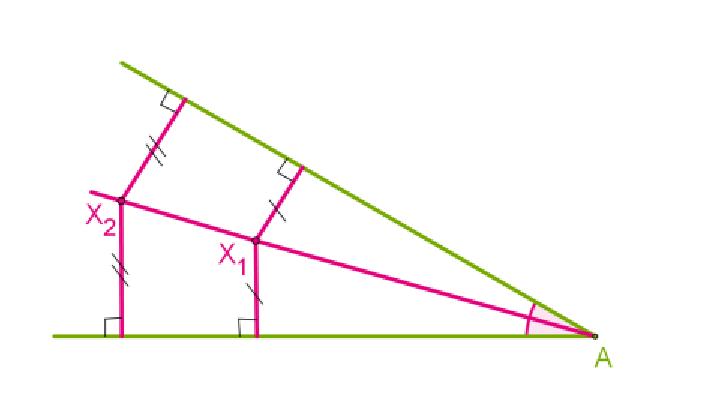
Теперь, разобравшись, как построить биссектрису данного угла, стоит вспомнить еще одно определение биссектрисы, используя термин "геометрическое место точек". Биссектрисой называется геометрическое место точек, которые равноудалены от лучей, образующих угол.
Согласно выполненному построению в пунктах 4-6, точка, принадлежащая построенной биссектрисе, также принадлежит двум окружностям, равным по радиусу, центр которых располагается на лучах, образующих угол на одинаковом расстоянии от вершины угла (согласно пунктам 1-3 построения). Опустим перпендикуляр из отмеченной в пункте 6 точки на лучи, образующие угол. Докажем, что получившиеся прямоугольные треугольники равны, и выясним, что опущенные перпендикуляры также равны, как соответствующие элементы треугольников. Таким образом, их общая гипотенуза является биссектрисой угла по определению. Что и требовалось доказать.