
Дисциплина "высшая математика" у некоторых вызывает неприятие, так как поистине не всем дано ее понять. Но те, кому посчастливилось изучать этот предмет и решать задачи, используя различные уравнения и коэффициенты, могут похвастаться практически полной в ней осведемленности. В психологической науке существует не только гуманитарная направленность, но и определенные формулы и способы для математической проверки выдвигаемой в ходе исследований гипотезы. Для этого применяются различные коэффициенты.
Коэффициент корреляции Спирмена
Это распространенное измерение по определению тесноты связи между какими-либо двумя признаками. Коэффициент еще называют непараметрическим методом. Он показывает статистику связи. То есть мы знаем, например, что у ребенка агрессия и раздражительность связаны между собой, а коэффициент корреляции рангов Спирмена показывает статистическую математическую связь этих двух признаков.
Как вычисляется ранговый коэффициент?
Естественно, что для всех математических определений или величин существуют свои формулы, по которым они вычисляются. Ею обладает и коэффициент корреляции Спирмена. Формула у него следующая:
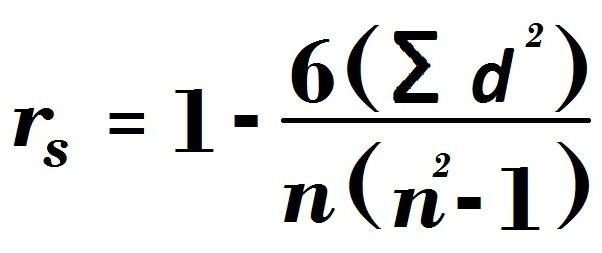
С первого взгляда формула не совсем понятна, но если разобраться, все очень легко вычисляется:
- n - это количество признаков или показателей, которые проранжированы.
- d - разность определенных двух рангов, соответствующих конкретным двум переменным каждого испытуемого.
- ∑d2 - сумма всех квадратов разностей рангов признака, квадраты которых вычисляются отдельно для каждого ранга.

Область применения математической меры связи
Для применения рангового коэффициента необходимо, чтобы количественные данные признака были проранжированы, то есть им был присвоен определенный номер в зависимости от места, на котором расположен признак, и от его значения. Доказано, что два ряда признаков, выраженных в числовом виде, несколько параллельны между собой. Коэффициент ранговой корреляции Спирмена определяет степень этой параллельности, тесноты связи признаков.
Для математической операции по расчету и определению связи признаков с помощью указанного коэффициента нужно произвести некоторые действия:
- Каждому значению какого-либо испытуемого или явления присваивается номер по порядку - ранг. Он может соответствовать значению явления по возрастанию и по убыванию.
- Дальше сопоставляются ранги значения признаков двух количественных рядов для того, чтобы определить разность между ними.
- В отдельном столбце таблицы для каждой полученной разности прописывается ее квадрат, а внизу результаты суммируются.
- После этих действий применяется формула, по которой рассчитывается коэффициент корреляции Спирмена.
Свойства коэффициента корреляции
К основным свойствам коэффициента Спирмена относят следующие:
- Измерение значений в пределах от -1 до 1.
- Знак коэффициента интерпретаций не имеет.
- Теснота связи определяется по принципу: чем выше величина, тем теснее связь.
Как проверить полученное значение?
Для проверки связи признаков между собой необходимо выполнить определенные действия:
- Выдвигается нулевая гипотеза (H0), она же основная, затем формулируется другая, альтернативная первой (H1). Первая гипотеза будет заключаться в том, что коэффициент корреляции Спирмена равняется 0 - это значит, что связи не будет. Вторая, наоборот, гласит, что коэффициент не равен 0, тогда связь есть.
- Следующим действием будет нахождение наблюдаемого значения критерия. Оно находится по основной формуле коэффициента Спирмена.
- Далее находятся критические значения заданного критерия. Это можно сделать только с помощью специальной таблицы, где отображаются различные значения по заданным показателям: уровень значимости (l) и число, определяющее объем выборки (n).
- Теперь нужно сравнить два полученных значения: установленного наблюдаемого, а также критического. Для этого необходимо построить критическую область. Нужно начертить прямую линию, на ней отметить точки критического значения коэффициента со знаком "-" и со знаком"+". Слева и справа от критических значений полукругами от точек откладываются критические области. Посередине, объединяя два значения, отмечается полукругом ОПГ.
- После этого делается вывод о тесноте связи между двумя признаками.
Где лучше использовать эту величину
Самой первой наукой, где активно использовался этот коэффициент, была психология. Ведь это наука, не основывающаяся на цифрах, однако для доказательства каких-либо важных гипотез, касающихся развития отношений, черт характера людей, знаний студентов, требуется статистическое подтверждение выводов. Также его используют в экономике, в частности, при валютных оборотах. Здесь оцениваются признаки без статистики. Очень удобен коэффициент ранговой корреляции Спирмена в этой области применения тем, что оценка производится независимо от распределения переменных, так как они заменяются ранговым числом. Активно применяется коэффициент Спирмена в банковском деле. Социология, политология, демография и другие науки также используют его в своих исследованиях. Результаты получаются быстро и максимально точно.
Удобно и быстро используется коэффициент корреляции Спирмена в Excel. Здесь существуют специальные функции, которые помогают быстро получить необходимые значения.
Какие еще коэффициенты корреляции существуют?
Кроме того, что мы узнали про коэффициент корреляции Спирмена, существуют еще различные корреляционные коэффициенты, позволяющие измерить, оценить качественные признаки, связь между количественными признаками, тесноту связи между ними, представленными в ранговой шкале. Это такие коэффициенты, как биссериальный, рангово-биссериальный, контенгенции, ассоциации, и так далее. Коэффициент Спирмена очень точно показывает тесноту связи, в отличие от всех остальных методов ее математического определения.


























