Коэффициент Шарпа: определение, правила расчета и формула

Коэффициент Шарпа показывает, как соотносятся доходность инвестиционного портфеля и риск. Данный коэффициент интересен для инвесторов, которые сравнивают торговые стратегии или финансовые инструменты.

Сущность показателя

Коэффициент Шарпа показывает работоспособность используемой торговой стратегии или финансового инструмента. Чем он выше, тем более эффективен объект оценки.

Данные этого коэффициента показывают как показатель прошлых оценок прибыльности к риску, так и прогнозируют уровень стабильности потенциальной прибыли. В связи с этим он чаще всего применяется финансовыми аналитиками в сводных таблицах, в которых приводится оценка активов.

Проведение расчета

Расчет коэффициента показывает инвестору, какая степень риска присуща определенному активу. Рассчитывают коэффициент Шарпа по формуле, указанной в статье.

• Rx - среднее значение прибыли.
• Rf - наилучшая доступная норма прибыли безрисковой обеспеченности.
• StdDev - стандартное отклонение прибыльности актива.
• X - инвестиции.

При расчете коэффициента Шарпа в числителе используется математическое ожидание.

Как любой коэффициент, данный показатель является безразмерной величиной. Наиболее часто его данные сравниваются с бенчмарком, который представляет собой безрисковую процентную ставку доходности актива.

Расчет прибыльности безрискового актива

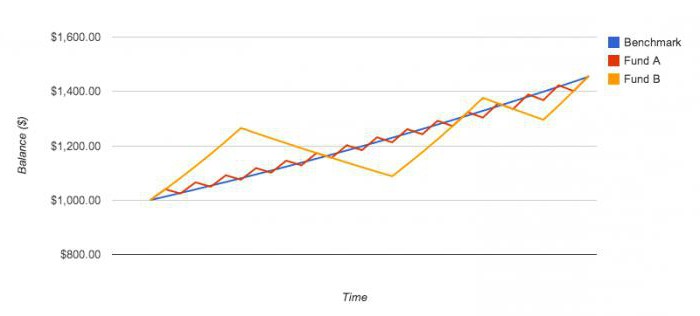
Инвестор хочет получить большую доходность по сравнению с той, которую он мог бы получить, если бы вкладывался только в полностью надежные активы. Эта большая доходность называется избыточной. Последняя характеризует качество менеджмента и эффективность принимаемых решений инвестором.

Прибыль актива с нулевым риском может быть оценена несколькими способами:

• Доходность банковских депозитов самых крупных и надежных отечественных банков, прежде всего, Сбербанка и ВТБ24.
• Доходность государственных ценных бумаг с нулевым риском (к этим бумагам относятся ОФЗ и ГКО в РФ, десятилетние облигации в США), обладающие максимальной надежностью по мнению рейтинговых агентств S&P, Moody's, Fitch.

Оценка коэффициента Шарпа

Если рассчитанное значение больше 1, это свидетельствует о том, что для портфеля или актива характерна высокая доходность, что делает его привлекательным для инвестиций.

При нахождении рассчитанного значения в диапазоне от 0 до 1 можно говорить о том, что степень риска выше величины избыточной доходности. Здесь, помимо коэффициента Шарпа, нужно оценить и иные показатели инвестиционной привлекательности.

Если рассчитанное значение меньше 1, это свидетельствует о том, что избыточная доходность принимает отрицательные величины, лучше предпочесть актив с минимальным уровнем риска.

Если сравниваются два рассматриваемых коэффициента, и один превышает другой, то говорят, что первый портфель (актив) более привлекателен для инвестора по сравнению со вторым.

Пример оценки

При формировании инвестиционного портфеля необходимо осуществить сравнительный анализ разных портфелей. Для этого необходимо знать котировки всех ценных бумаг этого портфеля. Облегчить расчет может помочь программа MS Excel. Рассмотрим пример расчета коэффициента Шарпа на основе виртуальных компаний.

Предположим, что в наш портфель входят акции трех компаний: А, Б, В. Доля в портфеле компании А составляет 30 %, компании Б - 25 % и компании В - 40 %. Возьмем для примера котировки в течение одной недели, хотя в реальности нужно оценивать за более продолжительный промежуток времени (месяц, квартал, год).

Вводим в электронную таблицу данные по котировкам всех трех компаний за оцениваемый период. Далее, рассчитываем доходность ценных бумаг каждой сравниваемой компании, для чего в ячейки вводим формулу нахождения натурального логарифма отношения каждого последующего дня к предыдущему, например, в ячейке Е4 вводим =LN(B4/B3)*100, протягиваем (или копируем формулу и вставляем в последующие ячейки) вниз и вправо.

Далее рассчитываем доходность портфеля, его риск и оцениваем доходность безрискового актива. В качестве последней величины примем процентную ставку по депозитам (8 %). Доходность портфеля рассчитываем по формуле = СР. ЗНАЧ (E4:E9)*B1+СР. ЗНАЧ (F4:F9)*C1+СР. ЗНАЧ (G4:G9)*D1 (полученная величина одна, ничего протягивать или копировать не нужно).

Риск портфеля рассчитываем по формуле = СТАНД. ОТКЛОН (E4:E9)*B1+СТАНД. ОТКЛОН (F4:F9)*C1+СТАНД. ОТКЛОН(G4:G9)*D1

Коэффициент Шарпа рассчитываем, как = (H4-J4)/I4.

Модифицированный коэффициент

В данном варианте расчета коэффициента Шарпа вместо стандартного отклонения применяется модифицированная мера риска, которая позволяет провести оценку потенциальных рисков динамики распределения прибыльности активов.

В данном случае расчет выполняется по формуле, указанной в статье.

• r_p – средняя прибыльность портфеля (актива);
• r_f – средняя прибыльность актива с нулевым риском;
• σ_p – стандартное отклонение прибыльностей актива (портфеля);
• S –эксцесс распределения прибыльностей;
• z_c – куртозис распределения прибыльностей актива (портфеля);
• K – квантиль распределения того же показателя.

Данная модель включает в себя исключительно статистический расчет, что повышает адекватность оценки риска.

Недостатки коэффициента Шарпа

Основным достоинством данного коэффициента является то, что при его использовании можно увидеть, какой финансовый инструмент будет обеспечивать более плавную прибыльность, а какой - скачкообразную.

Но коэффициент не лишен недостатков, основных из которых 3:

1. С его помощью рассчитывается усредненная прибыль в процентах за период, что в случае серии убыточных периодов является некорректным.
2. При использовании данного коэффициента резкое колебание в любую сторону имеет негативный оттенок, поскольку рассматривается как риск.
3. При расчете данного коэффициента серии убыточных и прибыльных сделок не учитываются, а это необходимо для оценивания эффективности торговли.

Коэффициент Сортино

Для нивелирования второго недостатка коэффициента Шарпа Сортино предложил его модификацию. У Шарпа рассматриваемый показатель учитывает как риск и положительные, и отрицательные изменения доходности. Коэффициент Сортино учитывает только отрицательные тенденции. Рассчитывается он так же, как и основной коэффициент, рассматриваемый в данной статье, но учитывается волатильность по прибыльностям актива или портфеля ниже минимально допустимой степени прибыльности.

В заключение

Таким образом, коэффициент Шарпа является статистическим показателем стабильности дохода актива (портфеля). В случае если инвестор хочет учитывать только отрицательную динамику в изменении доходности, необходимо использовать коэффициент Сортино.