Момент сил относительно оси вращения: основные понятия, формулы, пример решения задачи

Когда решают задачи на перемещение объектов, то в ряде случаев пренебрегают их пространственными размерами, вводя понятие материальной точки. Для другого типа задач, в которых рассматриваются покоящиеся или вращающиеся тела, важно знать их параметры и точки приложения внешних сил. В этом случае речь идет о моменте сил относительно оси вращения. Рассмотрим этот вопрос в статье.

Понятие о моменте силы

Перед тем как приводить формулу момента силы относительно оси вращения неподвижной, необходимо пояснить, о каком явлении пойдет речь. Ниже дан рисунок, на котором изображен гаечный ключ длиной d, к концу его приложена сила F. Нетрудно представить, что результатом ее воздействия будет вращение ключа против часовой стрелки и откручивание гайки.

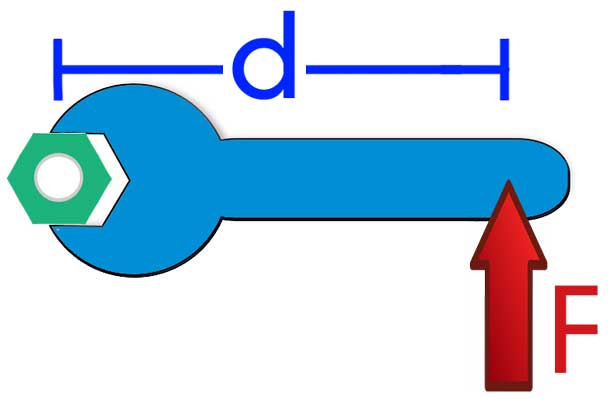
Согласно определению, момент силы относительно оси вращения представляет собой произведение плеча (d в данном случае) на силу (F), то есть можно записать следующее выражение: M = d*F. Сразу же следует оговориться, что приведенная формула записана в скалярном виде, то есть она позволяет рассчитать абсолютное значение момента M. Как видно из формулы, единицей измерения рассматриваемой величины являются ньютоны на метр (Н*м).

Момент силы - векторная величина

Как выше было оговорено, момент M в действительности представляет собой вектор. Для пояснения этого утверждения рассмотрим другой рисунок.

Здесь мы видим рычаг длиной L, который закреплен на оси (показано стрелкой). К его концу приложена сила F под углом Φ. Нетрудно себе представить, что эта сила будет вызывать подъем рычага. Формула для момента в векторной форме в этом случае запишется так: M¯ = L¯*F¯, здесь черта над символом означает, что рассматриваемая величина - это вектор. Следует пояснить, что L¯ направлен от оси вращения к точке приложения силы F¯.

Приведенное выражение является векторным произведением. Его результирующий вектор (M¯) будет направлен перпендикулярно плоскости, образованной L¯ и F¯. Для определения направления момента M¯ существуют несколько правил (правой руки, буравчика). Чтобы не заучивать их и не путаться в порядке умножения векторов L¯ и F¯ (от него зависит направление M¯), следует запомнить одну простую вещь: момент силы будет направлен таким образом, что если смотреть с конца его вектора, то воздействующая сила F¯ будет вращать рычаг против часовой стрелки. Это направление момента условно принято за положительное. Если же система совершает вращение по часовой стрелки, значит, результирующий момент сил имеет отрицательное значение.

Таким образом, в рассматриваемом случае с рычагом L величина M¯ направлена вверх (от рисунка к читателю).

В скалярной форме формула для момента запишется в виде: M = L*F*sin(180-Φ) или M = L*F*sin(Φ) (sin(180-Φ) = sin(Φ)). Согласно определению синуса, можно записать равенство: M = d*F, где d = L*sin(Φ) (см. рисунок и соответствующий прямоугольный треугольник). Последняя формула является аналогичной той, которая была приведена в предыдущем пункте.

Проведенные выше вычисления демонстрируют, как работать с векторными и скалярными величинами моментов сил, чтобы не допустить ошибок.

Физический смысл величины M¯

Поскольку два рассмотренных в предыдущих пунктах случая связаны с вращательным движением, то можно догадаться, какой смысл несет момент силы. Если сила, действующая на материальную точку, является мерой увеличения скорости линейного перемещения последней, то момент силы - это мера ее вращательной способности применительно к рассматриваемой системе.

Приведем наглядный пример. Любой человек открывает дверь, взявшись за ее ручку. Также это можно сделать, если толкнуть дверь в зоне ручки. Почему никто не открывает ее, толкая в области петель? Очень просто: чем ближе к петлям приложена сила, тем труднее открыть дверь, и наоборот. Вывод предыдущего предложения следует из формулы для момента (M = d*F), откуда видно, что при M = const величины d и F находятся в обратной зависимости.

Момент силы - аддитивная величина

Во всех рассмотренных выше случаях имела место лишь одна действующая сила. При решении же реальных задач дело обстоит гораздо сложнее. Обычно на системы, которые вращаются или находятся в равновесии, действуют несколько сил кручения, каждая из которых создает свой момент. В этом случае решение задач сводится к нахождению суммарного момента сил относительно оси вращения.

Суммарный момент находится путем обычной суммы отдельных моментов для каждой силы, однако, следует не забывать использовать правильный знак для каждого из них.

Пример решения задачи

Для закрепления полученных знаний предлагается решить следующую задачу: необходимо вычислить суммарный момент силы для системы, изображенной на рисунке ниже.

Мы видим, что на рычаг длиной 7 м действуют три силы (F1, F2, F3), причем они имеют разные точки приложения относительно оси вращения. Поскольку направление сил перпендикулярно рычагу, то нет необходимости применять векторное выражение для момента кручения. Можно рассчитать суммарный момент M, используя скалярную формулу и не забывая о постановке нужного знака. Поскольку силы F1 и F3 стремятся повернуть рычаг против часовой стрелки, а F2 - по часовой стрелке, то момент вращения для первых будет положительным, а для второй - отрицательным. Имеем: M = F1*7-F2*5+F3*3 = 140-50+75 = 165 Н*м. То есть суммарный момент является положительным и направлен вверх (на читателя).