Что это - прямая призма? Свойства и формулы. Пример задачи

Изучением характеристик трехмерных геометрических фигур занимается стереометрия. Одна из известных объемных фигур, которая появляется в задачах по геометрии, - это прямая призма. Рассмотрим в данной статье, что она собой представляет, а также подробно охарактеризуем призму с треугольным основанием.

Призма и ее виды

Под призмой подразумевают такую фигуру, которая образуется в результате параллельного переноса многоугольника в пространстве. В результате этой геометрической операции образуется фигура, состоящая из нескольких параллелограммов и двух одинаковых параллельных друг другу многоугольников. Параллелограммы являются боковыми сторонами призмы, а многоугольники - это ее основания.

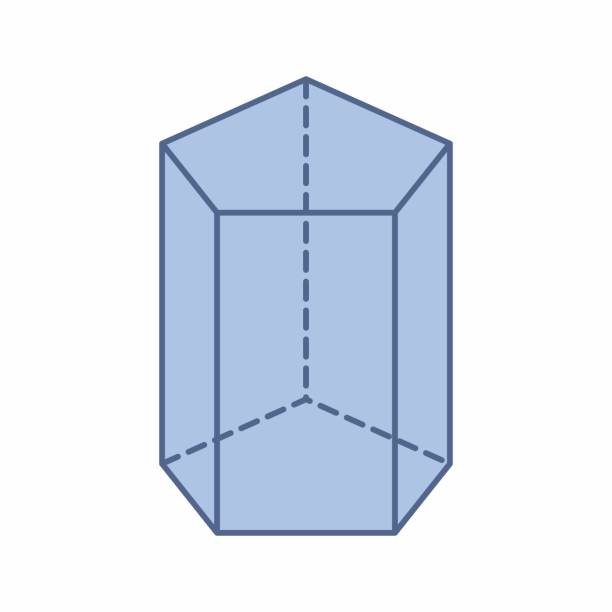
Любая призма имеет n+2 стороны, 3*n ребер и 2*n вершин, где n - число углов или сторон многоугольного основания. На изображении показана пятиугольная призма, которая состоит из 7 сторон, 10 вершин и 15 ребер.

Рассматриваемый класс фигур представлен призмами нескольких видов. Перечислим их кратко:

• вогнутые и выпуклые;
• наклонные и прямые;
• неправильные и правильные.

Каждая фигура относится к одному из перечисленных трех видов классификации. Во время решения геометрических задач проще всего выполнять расчеты для правильных и прямых призм. Последние подробнее рассмотрим в следующих пунктах статьи.

Что это - призма прямая?

Прямой называется вогнутая или выпуклая, правильная или неправильная призма, у которой все боковые стороны представлены четырехугольниками с углами 90°. Если хотя бы один из четырехугольников боковых сторон не будет прямоугольником или квадратом, то призма называется наклонной. Можно также дать другое определение: прямая призма - это такая фигура данного класса, у которой любое боковое ребро равно высоте. Под высотой h призмы полагают дистанцию между ее основаниями.

Оба приведенных определения того, что это - прямая призма, являются равноправными и самодостаточными. Из них следует, что все двугранные углы между любым из оснований и каждой боковой стороной равны 90°.

Выше было сказано, что с прямыми фигурами удобно работать при решении задач. Это связано с тем, что высота совпадает с длиной бокового ребра. Последний факт облегчает процесс вычисления объема фигуры и площади ее боковой поверхности.

Объем прямой призмы

Объем - свойственная любой пространственной фигуре величина, которая численно отражает часть пространства, заключенного между поверхностями рассматриваемого объекта. Объем призмы может быть рассчитан по следующей общей формуле:

V = S_o*h.

То есть произведение высоты на площадь основания даст искомое значение V. Поскольку у прямой призмы основания равны, то для определения площади S_o можно брать любое из них.

Преимущество использования приведенной выше формулы именно для прямой призмы в сравнении с другими ее видами заключается в том, что высоту фигуры найти очень просто, так как она совпадает с длиной бокового ребра.

Площадь боковой поверхности

Удобно рассчитывать не только объем для прямой фигуры рассматриваемого класса, но также ее боковую поверхность. Действительно, любая ее боковая сторона - это либо прямоугольник, либо квадрат. Как вычислить площадь этих плоских фигур, знает каждый школьник, для этого необходимо умножить смежные стороны друг на друга.

Предположим, что в основании призмы лежит произвольный n-угольник, стороны которого равны a_i. Индекс i пробегает значения от 1 до n. Площадь одного прямоугольника вычисляется так:

S_i = a_i*h.

Площадь поверхности боковой S_b нетрудно вычислить, если сложить все площади S_i прямоугольников. В таком случае получаем конечную формулу для S_b прямой призмы:

S_b = h*∑_i=1ⁿ(a_i) = h*P_o.

Таким образом, чтобы определить площадь боковой поверхности для прямой призмы, необходимо умножить ее высоту на периметр одного основания.

Задача с треугольной призмой

Предположим, что задана прямая призма. Основание - прямоугольный треугольник. Катеты этого треугольника равны 12 см и 8 см. Необходимо рассчитать объем фигуры и ее полную площадь, если высота призмы составляет 15 см.

Для начала вычислим объем прямой призмы. Треугольник (прямоугольный), находящийся в ее основаниях, имеет площадь:

S_o = a₁*a₂/2 = 12*8/2 = 48 см².

Как можно догадаться, a₁ и a₂ в этом равенстве являются катетами. Зная площадь основания и высоту (см. условие задачи), можно воспользоваться формулой для V:

V = S_o*h = 48*15 = 720 см³.

Полная площадь фигуры образована двумя частями: площадями оснований и боковой поверхностью. Площади двух оснований равны:

S_2o = 2*S_o = 48*2 = 96 см².

Для вычисления площади боковой поверхности необходимо знать периметр прямоугольного треугольника. Вычислим по теореме Пифагора его гипотенузу a₃, имеем:

a₃ = √(a₁² + a₂²) = √(12² + 8²) = 14,42 см.

Тогда периметр треугольника основания прямой призмы составит:

P = a₁ + a₂ + a₃ = 12 + 8 + 14,42 = 34,42 см.

Применяя формулу для S_b, которая была записана в предыдущем пункте, получаем:

S_b = h*P = 15*34,42 = 516,3 см.

Сложив площади S_2o и S_b, мы получим полную площадь поверхности изучаемой геометрической фигуры:

S = S_2o + S_b = 96 + 516,3 = 612,3 см².

Треугольная призма, которую изготавливают из специальных видов стекла, применяется в оптике при изучении спектров излучающих свет объектов. Такие призмы способны разлагать свет на составляющие частоты благодаря явлению дисперсии.