Внешний угол правильного многоугольника: интересные факты о геометрии
Внешние углы многоугольников являются важной характеристикой при изучении их свойств. Особый интерес представляет рассмотрение внешних углов правильных многоугольников, поскольку здесь выполняются дополнительные соотношения. В данной статье мы познакомимся с определением внешнего угла многоугольника, рассмотрим его связь с внутренними углами фигуры. Далее изучим свойства внешних углов правильного многоугольника и выведем формулы для их вычисления.
Рассмотрим также конкретные примеры вычисления величины внешних углов у различных правильных многоугольников. Узнаем интересные факты о сумме внешних углов выпуклых многоугольников и ее связи с количеством сторон фигуры. В заключение приведем примеры применения полученных знаний о внешних углах правильных многоугольников на практике.
Что такое внешний угол многоугольника
Внешний угол многоугольника - это угол, образованный продолжением одной из сторон многоугольника и смежной с ней стороной. В отличие от внутреннего угла, который измеряется внутри многоугольника, внешний угол измеряется с внешней стороны многоугольника. При этом внешний угол равен разности между 180° и внутренним смежным углом. То есть если внутренний угол равен α, то внешний угол будет равен 180° - α.
Внешний угол правильного многоугольника имеет равную величину при каждой вершине фигуры. Это связано с тем, что в правильном многоугольнике все стороны и все внутренние углы равны. Соответственно, если из внутреннего угла α вычесть постоянную величину (180°), то и разности при всех вершинах будут равны.
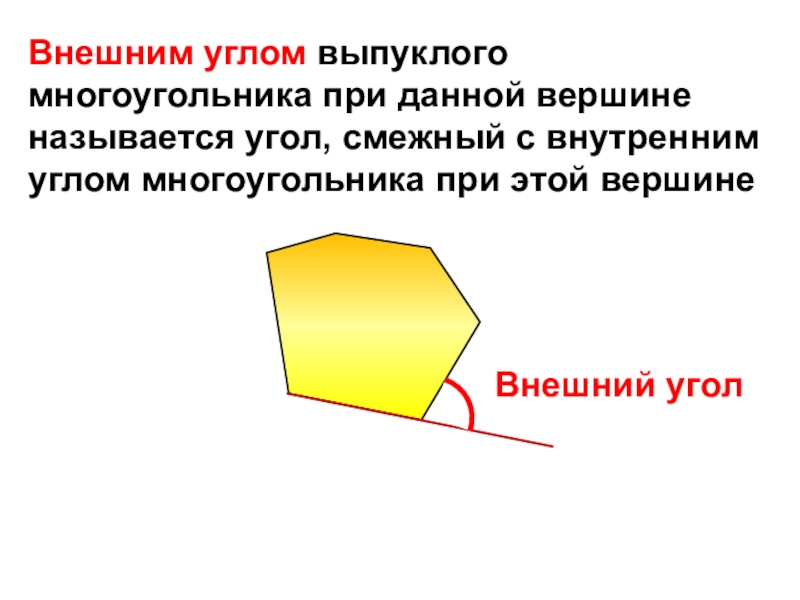
Свойства внешних углов правильного многоугольника
Одним из важных свойств внешних углов правильного многоугольника является то, что их сумма всегда равна 360°. Это можно доказать, рассмотрев сумму внешних и внутренних углов.
Внутренние углы правильного многоугольника равны друг другу, их обозначим через α. Тогда сумма всех внутренних углов будет равна n·α, где n - число сторон. Известно, что сумма внутренних углов выпуклого многоугольника равна (n-2)·180°.
Следовательно, n·α = (n-2)·180°. Внешний угол при каждой вершине равен 180°- α. Тогда сумма всех внешних углов: n·(180°- α) = n·180° - n·α = 360°.
Примеры конкретных значений внешних углов
Рассмотрим несколько конкретных примеров, чтобы проиллюстрировать как вычисляются внешние углы для разных правильных многоугольников.
Возьмем правильный треугольник. У него 3 стороны и все внутренние углы равны 60°. Соответственно, внешний угол будет равен 180° - 60° = 120°.
Для квадрата, у которого 4 равные стороны и 4 равных внутренних угла по 90°, внешний угол составит 180° - 90° = 90°.
В правильном пятиугольнике 5 равных сторон и 5 равных внутренних углов по 108°. Отсюда внешний угол равен 180° - 108° = 72°.
Аналогично можно посчитать для правильного шестиугольника (внутренний 120°, внешний 60°), семиугольника (внутренний 128,6°, внешний 51,4°) и т.д. При увеличении числа сторон, внутренние углы становятся ближе к 180°, а внешние - к 0°.
Применение знаний о внешних углах на практике
Знания о внешних углах правильных многоугольников применяются для решения множества геометрических задач. Рассмотрим несколько примеров.
Например, если требуется найти угол между сторонами правильного многоугольника, это легко сделать через внешний угол. Если известно число сторон n, то внутренний угол α = (n-2)*180/n градусов. Тогда искомый угол между сторонами будет равен 360/n градусов.
Также по формуле для внешнего угла можно определить число сторон правильного многоугольника, если известна величина этого угла. Например, если внешний угол равен 120°, значит он образован правильным треугольником.
Еще одно применение - вычисление площади правильного многоугольника через сторону a и внешний угол β: S = (na^2)/(4tan(β)). Это следует из формулы для площади через радиус вписанной окружности.
Знание свойств внешних углов помогает также решать задачи на построение правильных многоугольников. Например, для построения правильного шестиугольника достаточно отложить сторону, равную радиусу описанной окружности, и с помощью циркуля и линейки построить внешние углы в 60°.
