Знание момента инерции тела позволяет воспользоваться законом сохранения момента импульса либо выражением для описания кругового движения с угловым ускорением. В данной статье рассмотрим, как находить для цилиндра момент инерции при различном положении осей вращения.
Момент инерции: математическое определение
Осевой момент инерции вводится в физику благодаря изучению законов вращательного движения тел. Для точки материальной с массой m, вращающейся на расстоянии r от оси, момент инерции будет равен:
I = m*r2
В общем же случае для тела, которое имеет произвольное распределение вещества в пространстве (любую геометрическую форму), величину I можно вычислить так:
I = ∫r2dm
По сути, это выражение является обобщением предыдущего. В нем производится суммирование (интегрирование) моментов от каждой элементарной частицы dm, дистанция до оси от которой равна r.
Если говорить о физическом значении рассматриваемой величины I, то она показывает, насколько "сильно" система сопротивляется воздействию внешнего момента силы, который пытается ее раскрутить или, наоборот, остановить.
Момент инерции цилиндра относительно оси, его основаниям перпендикулярной
Из приведенной выше формулы можно понять, что величина I является характеристикой всей вращающейся системы, то есть она зависит как от формы тела и распределения в нем массы, так и от относительного положения оси.
В данном пункте рассмотрим простой случай: определить необходимо момент инерции для сплошного цилиндра, ось вращения которого перпендикулярна его основаниям и проходит через гравитационный центр фигуры.
Для решения проблемы применим интегральную формулу для I. В процессе операции интегрирования мысленно разобьем цилиндр на тонкие колечки толщиной dr. Каждое колечко будет иметь объем: dV = 2*pi*r*dr*h, здесь h - высота фигуры. Учитывая, что dm = ρ*dV, где ρ - плотность цилиндра, получаем:
I = ∫r2dm = ρ*∫r2dV = 2*pi*ρ*h*∫r3dr
Этот интеграл необходимо вычислить для пределов от 0 до R, где R - радиус фигуры. Тогда получим:
I = 2*pi*ρ*h*∫R0r3dr = 2*pi*ρ*h/4*(r4)∣R0 = pi*ρ*h*R4/2
Воспользовавшись формулой для массы цилиндра через его объем и плотность, приходим к конечному выражению:
I = m*R2/2, где m = pi*ρ*h*R2
Мы получили формулу инерции момента цилиндра однородного. Она показывает, что величина I для этой фигуры в 2 раза меньше, чем для материальной точки аналогичной массы, которая вращается на расстоянии радиуса цилиндра от оси.
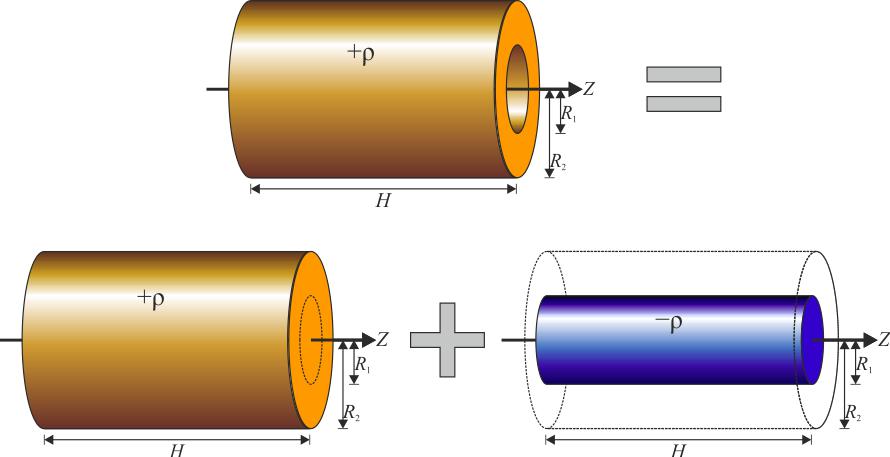
Момент инерции полого цилиндра
Теперь оставим ось на том же месте и найдем значение I для цилиндра с пустотой внутри (втулка, труба). Такую фигуру описывают двумя радиусами: внешним R1 и внутренним R2. В этом случае для интегрирования применяется абсолютно тот же подход, что и для сплошного цилиндра, только пределы теперь изменяются от R2 до R1. Имеем:
I = 2*pi*ρ*h/4*(r4)∣R1R2 = pi*ρ*h*R4/2∣R1R2 = pi*ρ*h/2*(R14-R24)
Для дальнейшего упрощения этой формулы воспользуемся разложением на множители выражения в скобках, получим:
I = pi*ρ*h*(R12-R22)*(R12+R22)/2
Часть этого выражения вместе с первыми скобками является массой полого цилиндра, поэтому получаем конечную формулу:
I = m*(R12+R22)/2
Отсюда видно, что момент инерции полого цилиндра больше этого значения для сплошного цилиндра аналогичной массы и такого же внешнего радиуса на величину m*R22/2. Этот результат не вызывает удивления, поскольку в полом цилиндре центр масс находится от оси вращения дальше, чем в сплошном.

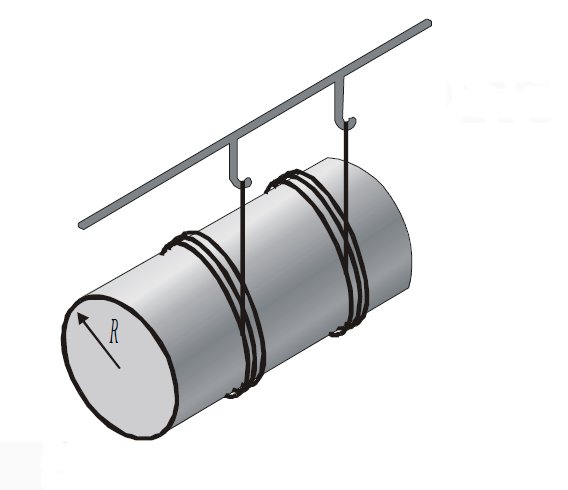
Величина I для цилиндра, ось вращения которого проходит параллельно плоскостям его основания
В такой системе ось вращения проходит также через центр массы цилиндра, но теперь он лежит как бы на боку (на цилиндрической поверхности, см. рис. ниже).
Расчет для момента инерции цилиндра для такой ситуации является непростой задачей, поскольку требует наличия дополнительных знаний для ее решения. Тем не менее приведем необходимые математические выкладки, чтобы читатели имели более полное представление о проведении интегрирования при вычислении I.
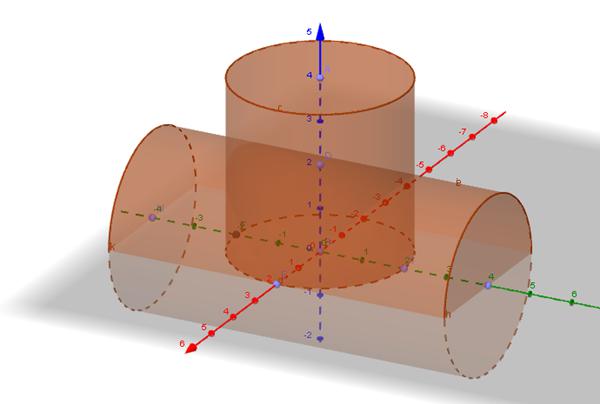
Начинаем решать задачу. Разбиваем сплошной цилиндр на отдельные диски бесконечно малой толщины. Чтобы узнать, каким моментом инерции обладает этот диск относительно оси, которая проходит через него и параллельна его основаниям, необходимо выполнить отдельное интегрирование. Оно дает следующий результат:
Ii = R2*dm/4
Чтобы найти, величину Ii для этого диска относительно уже новой оси, которая рассматривается в задаче, необходимо воспользоваться теоремой Штейнера. Получим:
Ii = R2*dm/4 + L2*dm, здесь L - расстояние от оси до тонкого диска.
Зная, что dm = pi*R2*dL*ρ, подставляем в интегральную формулу для I и проводим интегрирование по пределам (-L0/2; +L0/2), имеем:
I = ∫mIi = ∫m(R2*dm/4 + L2*dm) = pi*R2*ρ*∫L0/2-L0/2(R2*dL/4 + L2*dL)
Решение этого интеграла приводит к конечной формуле:
I = m*(R2/4 + L02/12)
Пример решения задачи
Решим интересную задачу на нахождение осевого момента инерции цилиндра. Пусть он лежит на цилиндрической поверхности, а ось вращения расположена параллельно его основанию и проходит через конец фигуры.
Эта ситуация полностью аналогична рассмотренной в предыдущем пункте, только ось пересекает не гравитационный центр цилиндра, а конец этой фигуры. Тем не менее для решения проблемы можно воспользоваться результатом предыдущего пункта статьи. Применим вышеупомянутую теорему Штейнера, получим:
I = m*R2/4 + m*L02/12 + m*(L0/2)2 = m*R2/4 + m*L02/3
Заметим, что если R<<L0, тогда первым слагаемым можно пренебречь, и формула сводится к равенству:
I = m*L02/3
Этот момент инерции соответствует стержню с осью вращения на его конце.