Перевод из двоичной в десятичную систему счисления: правило, примеры

Перевод чисел из двоичной системы счисления в десятичную является важным навыком для понимания работы компьютеров и других цифровых устройств. Компьютеры используют двоичную систему для представления и обработки данных, однако людям проще работать с десятичными числами. Давайте разберемся, как перевести двоичное число в десятичное.

Правило перевода из двоичной системы в десятичную

Перевод основан на позиционном принципе записи чисел. Каждый разряд двоичного числа умножается на степень числа 2. Например, в числе 1101:

• 1 умножается на 2^3 = 8
• 1 умножается на 2^2 = 4
• 0 умножается на 2^1 = 0
• 1 умножается на 2^0 = 1

Складываем полученные произведения: 8 + 4 + 0 + 1 = 13. Таким образом, двоичное число 1101 в десятичной системе записывается как 13.

Пошаговый перевод из двоичной в десятичную с примерами

Давайте разберем пошаговый перевод двоичных чисел в десятичную систему на конкретных примерах.

1. Записываем двоичное число, например 1010.
2. Пишем степени числа 2 под каждым разрядом: 1*2^3, 0*2^2, 1*2^1, 0*2^0.
3. Перемножаем каждую цифру на соответствующую степень двойки.
4. Складываем полученные произведения: 1*8 + 0*4 + 1*2 + 0*1 = 10.

Другой пример - двоичное число 11100 переводится так:

1. 11100
2. 1*2^4, 1*2^3, 1*2^2, 0*2^1, 0*2^0
3. 1*16, 1*8, 1*4, 0*2, 0*1
4. 16 + 8 + 4 = 28

Итого, двоичное число 11100 в десятичной системе - это 28.

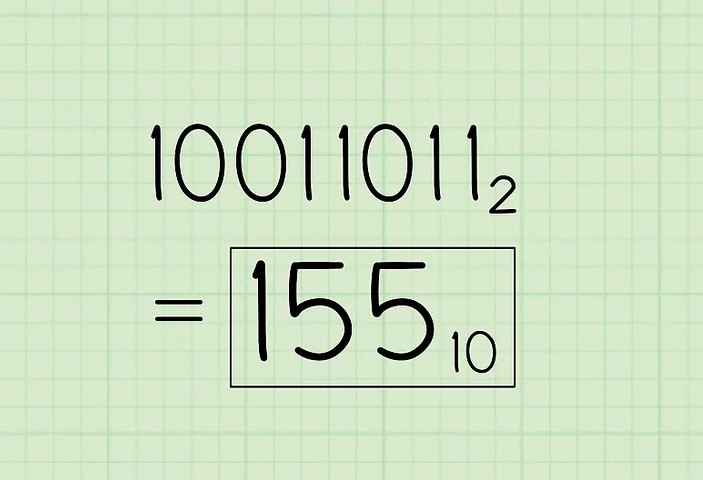
Обратный перевод из десятичной в двоичную

Чтобы перевести десятичное число в двоичную систему, нужно выполнить обратную операцию - деление десятичного числа на основание системы счисления (2). Остатки от деления записываются в обратном порядке и дают двоичное представление числа.

Способы перевода из двоичной в десятичную

Кроме ручного перевода существуют и другие способы:

• Использование калькулятора, который умеет переводить из одной системы счисления в другую.
• Специальные онлайн-конвертеры двоичного кода.
• Встроенные функции перевода в языках программирования и пакетах (например, bin2dec в Python).

Однако ручной перевод остается важным навыком для глубокого понимания принципов работы двоичной системы.

Где применяется перевод из двоичной системы

Перевод двоичных чисел в десятичную систему и обратно применяется во многих областях:

• Информатика и программирование - работа с двоичным кодом и двоичными файлами.
• Цифровая электроника - анализ логических схем, двоичных сигналов.
• Телекоммуникации - передача информации.
• Криптография - шифрование и дешифрование данных.
• Кодирование информации - сжатие данных, изображений, звука.

Владение навыками перевода помогает специалистам в этих областях эффективно работать с двоичным кодом, понимать принципы обработки информации в цифровых системах.

Интересные факты о двоичной системе

• В двоичной системе используются только две цифры - 0 и 1. Это связано с двумя состояниями транзистора в компьютерах - включено/выключено.
• Двоичная система называется двоичной, потому что в ней за основу взято число 2.
• Двоичная система была впервые подробно описана немецким математиком и философом Готфридом Вильгельмом Лейбницем в XVII веке.
• Самый большой недостаток двоичной системы - громоздкость записи больших чисел из-за использования только двух цифр.

Изучение двоичной системы счисления, ее особенностей и правил перевода помогает лучше понять устройство компьютеров и цифровых технологий, которые играют огромную роль в современном мире.

Рассмотрим более подробно некоторые практические аспекты перевода чисел из двоичной системы счисления в десятичную.

Перевод двоичных чисел с фиксированной запятой

Двоичные числа могут быть как целыми, так и дробными. Целые числа записываются как обычная последовательность двоичных цифр. Например, 11100 - это десятичное число 28.

Для записи дробных чисел используется фиксированная запятая. Она отделяет целую часть числа от дробной. Например, число 11,25 в двоичном представлении будет выглядеть так: 1011,01. Здесь целая часть - 1011, дробная часть после запятой - 01. Перевод осуществляется так же, как и для целых чисел.

Перевод отрицательных двоичных чисел

Существует несколько способов представления отрицательных чисел в двоичной системе. Рассмотрим два наиболее распространенных:

1. Прямой дополнительный код. Старший разряд используется как знаковый. 0 означает положительное число, 1 - отрицательное. Например, числу -5 соответствует двоичный код 101, который переводится как -5.
2. Обратный дополнительный код. Число инвертируется (все единицы меняются на нолики и наоборот), к результату прибавляется 1. Например, -5 = 101, инверсия 010, прибавляем 1: 011 = -5.

При переводе отрицательных чисел важно определить используемый способ кодирования, чтобы выполнить перевод корректно.

Перевод смешанных чисел

В некоторых задачах требуется перевести двоичное число, содержащее и целую, и дробную часть. Например, 1101,01. В этом случае перевод выполняется отдельно для каждой части:

1. 1101 (целая часть) = 13
2. 01 (дробная часть) = 0,25

Получаем десятичный результат: 13,25. Таким образом переводят смешанные двоичные числа, содержащие и целую и дробную часть.

Перевод с использованием дополнительного кода

Дополнительный код используется для представления отрицательных чисел. Правило перевода такое:

1. Перевести двоичное число как обычное положительное.
2. Если старший разряд 1, то полученное число берется со знаком минус.

Например, 1001 переводится как -7, а 0110 - как 6. Дополнительный код удобен для выполнения арифметических операций с отрицательными числами на компьютере.

Перевод двоично-десятичных чисел

Рассмотрим числа с дробной частью. В двоичной системе дробная часть отделяется запятой, например: 1010,1101. Переводим по разрядам:

1. 1010 (целая часть) = 10
2. 1101 (дробная часть) = 0,8125

Складываем результаты: 10 + 0,8125 = 10,8125. Так переводятся двоично-десятичные числа.

Автоматизация перевода двоичных чисел

Существуют программные средства, позволяющие автоматизировать перевод чисел из одной системы счисления в другую:

• Калькуляторы с поддержкой разных систем счисления.
• Специальные конвертеры чисел и кодов.
• Библиотеки и функции в языках программирования (Python, Java, C++ и др.).
• Онлайн сервисы перевода чисел.
• Мобильные приложения конвертеров.

Эти инструменты избавляют от рутинных вычислений и позволяют быстро переводить числа, в том числе объемные двоичные массивы данных.

Перевод и обработка потоков двоичных данных

Перевод используется при работе с потоками двоичных данных:

• Файлы, видео, аудио в двоичном формате.
• Потоки данных в компьютерных сетях.
• Шифрованные сообщения.

Данные читаются двоичными блоками, переводятся в десятичный вид, обрабатываются и могут конвертироваться обратно в двоичный поток. Такая конвертация необходима для интерпретации двоичных данных.

Перевод двоичных чисел в программировании

В программировании перевод двоичных чисел часто применяется при:

• Работе с битовыми операциями и флагами.
• Генерации случайных чисел.
• Хешировании и шифровании данных.
• Двоичной сериализации объектов.
• Вводе-выводе двоичных файлов и потоков.

Двоичные числа переводятся в десятичный вид для удобства отладки и вывода информации. При необходимости выполняется обратный перевод.

Перевод из двоичной в другие системы счисления

Помимо десятичной, перевод может выполняться и в другие системы счисления:

• Восьмеричная - использует цифры 0-7.
• Шестнадцатеричная - цифры 0-9 и буквы A-F.
• Разные позиционные системы в математике.

Перевод осуществляется аналогично, путем умножения каждого разряда на основание целевой системы счисления.

Ошибки при переводе двоичных чисел

Типичные ошибки:

• Неправильное определение позиций разрядов.
• Ошибки умножения разрядов на степени числа 2.
• Неверное сложение частичных результатов.
• Опечатки при записи двоичного или десятичного числа.

Чтобы их избежать, нужны внимательность, проверка вычислений и практика перевода чисел.