Формула для определения объема конуса. Пример решения задачи

Каждый школьник при изучении стереометрии в старших классах сталкивался с конусом. Двумя важными характеристиками этой пространственной фигуры являются площадь поверхности и объем. В данной статье покажем, как находить объем круглого конуса.

Круглый конус как фигура вращения прямоугольного треугольника

Прежде чем переходить непосредственно к теме статьи, следует описать конус с геометрической точки зрения.

Пусть имеется некоторый прямоугольный треугольник. Если его вращать вокруг любого из катетов, то результатом этого действия станет искомая фигура, изображенная ниже на рисунке.

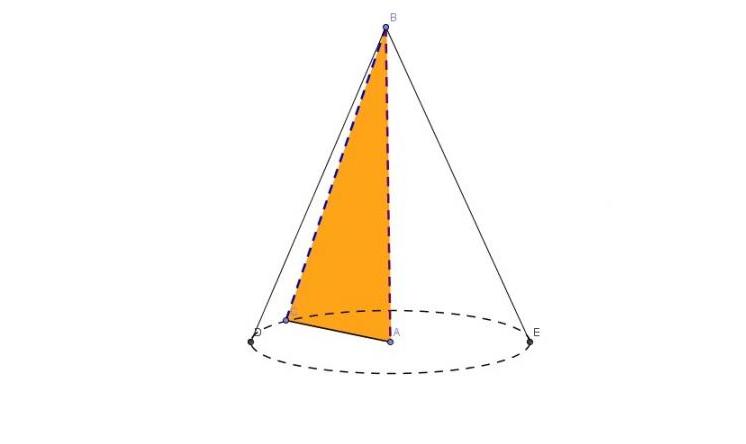
Здесь катет AB является частью оси конуса, а его длина соответствует высоте фигуры. Второй катет (отрезок CA) будет радиусом конуса. Во время вращения он опишет окружность, ограничивающую основание фигуры. Гипотенуза BC называется образующей фигуры, или ее генератрисой. Точка B - это вершина конуса, которая у него является единственной.

Учитывая свойства треугольника ABC, можно записать связь между генератрисой g, радиусом r и высотой h в виде следующего равенства:

g² = h² + r²

Эта формула оказывается полезной при решении многих геометрических задач с рассматриваемой фигурой.

Формула объема конуса

Объемом всякой пространственной фигуры называют область пространства, которую ограничивают поверхности этой фигуры. Для конуса таких поверхностей две:

1. Боковая, или коническая. Она образована всеми генератрисами.
2. Основание. В данном случае оно является кругом.

Получим формулу для определения объема конуса. Для этого разрежем его мысленно на множество параллельных основанию слоев. Каждый из слоев имеет толщину dx, которая стремится к нулю. Площадь S_x слоя, который находится на расстоянии x от вершины фигуры, равна следующему выражению:

S_x = pi*r²*x²/h²

Справедливость этого выражения можно проверить интуитивно, если подставить значения x = 0 и x = h. В первом случае мы получим равную нулю площадь, во втором случае она будет равна площади круглого основания.

Для определения объема конуса необходимо сложит маленькие "объемчики" каждого слоя, то есть следует воспользоваться интегральным исчислением:

V = ∫₀^h(pi*r²*x²/h²*dx) = pi*r²/h²*∫₀^h(x²*dx)

Вычисляя этот интеграл, приходим к конечной формуле для круглого конуса:

V = 1/3*pi*r²*h

Любопытно отметить, что эта формула полностью аналогична той, которая используется для вычисления объема произвольной пирамиды. Это совпадение не случайное, ведь любая пирамида переходит в конус при увеличении количества ее ребер до бесконечности.

Задача на вычисление объема

Полезно привести пример решения задачи, который продемонстрирует использование выведенной формулы для объема V.

Дан круглый конус, у которого площадь основания равна 37 см², а генератриса фигуры больше в три раза радиуса. Чему равен объем конуса?

Формулой для объема мы вправе воспользоваться, если знаем две величины: высоту h и радиус r. Найдем формулы, которые их определяют в соответствии с условием задачи.

Радиус r можно рассчитать, зная площадь круга S_o, имеем:

S_o = pi*r² =>

r = √(S_o/pi)

Пользуясь условием задачи, запишем равенство для генератрисы g:

g = 3*r = 3*√(S_o/pi)

Зная формулы для r и g, рассчитаем высоту h:

h = √(g² - r²) = √(9*S_o/pi - S_o/pi) = √(8*S_o/pi)

Мы нашли все необходимые параметры. Теперь пришло время подставить их в формулу для V:

V = 1/3*pi*r²*h = 1/3*pi*S_o/pi*√(8*S_o/pi) = S_o/3*√(8*S_o/pi)

Осталось подставить площадь основания S_o и вычислить значение объема: V = 119,75 см³.