Тангенс двойного угла: формулы и свойства

Тригонометрические функции, такие как тангенс, играют важную роль в математике, физике, инженерии и других областях. Умение оперировать ими, включая применение формул двойного угла, является полезным практическим навыком.

Основные понятия тригонометрии

Тригонометрические функции описывают соотношения между углами и сторонами в треугольнике. К основным относят:

• Синус - отношение противолежащего катета к гипотенузе
• Косинус - отношение прилежащего катета к гипотенузе
• Тангенс - отношение противолежащего катета к прилежащему

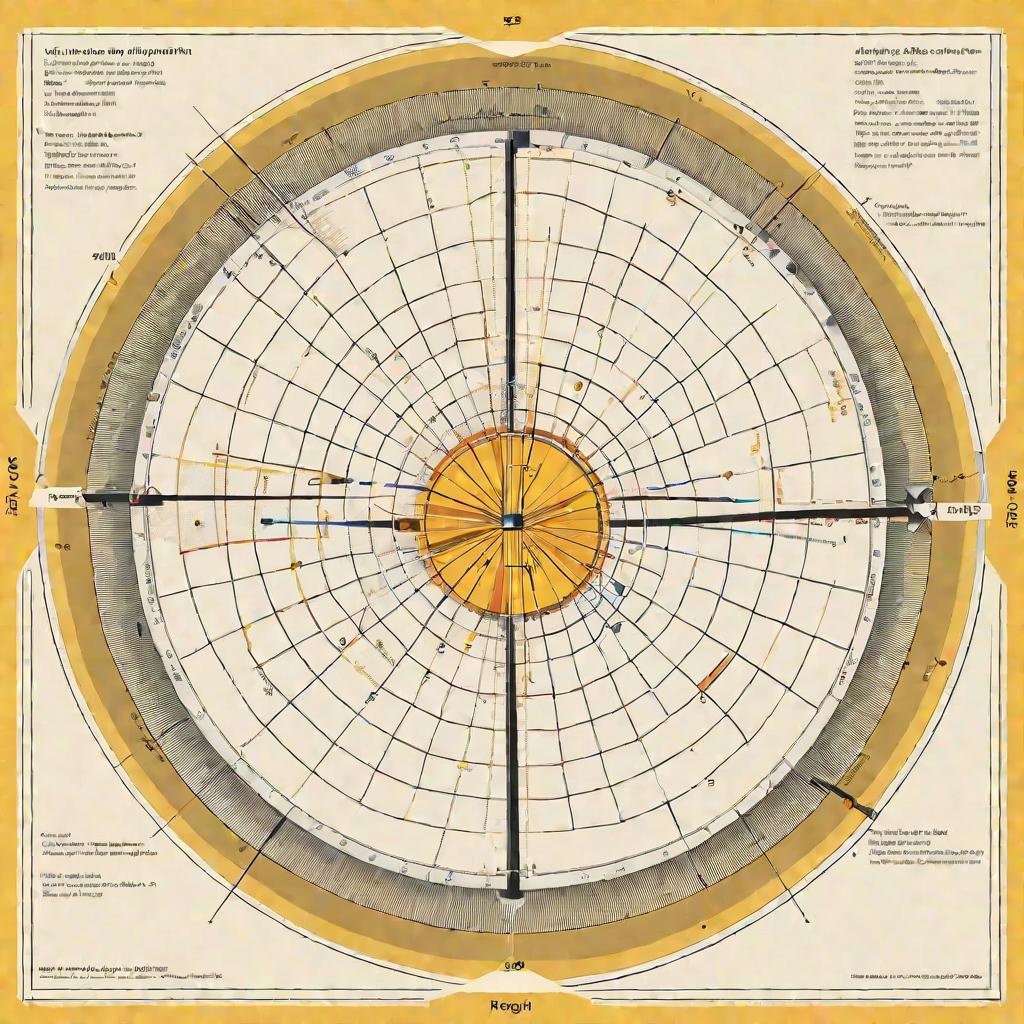
Для измерения углов используют тригонометрическую окружность с радиусом 1. Точки на окружности задают значения тригонометрических функций для данного угла. Например, для 30° имеем: sin 30° = 0,5; cos 30° = ^√3⁄₂; tg 30° = ^√3.

Формулы тангенса двойного и половинного угла

Тангенс двойного угла можно выразить через тангенс исходного угла:

tg 2α = ^{2tg α}⁄_{1 − tg² α}

Это следует из основного тригонометрического тождества. Тангенс обладает свойствами нечетной функции, поэтому знак tg 2α совпадает со знаком tg α. Однако выражение определено не при всех значениях α.

Аналогично для половинного угла имеем:

tg ^α⁄₂ = ^{tg α}⁄_{1 + tg² α}

При выводе используется тождество tg(α ± β) = ^{tg α ± tg β}⁄_{1 ∓ tg α tg β}.

Рассмотрим пример вычисления тангенса двойного угла. Пусть α = 20°, тогда:

Полученное значение совпадает со значением tg 40°.

Формулы позволяют также находить тангенс тройного, четверного и других кратных углов. Например, для тройного угла имеем:

tg 3α = ^{tg α}⁄_{(3 tg² α − 1)}

Практические задачи с тангенсом двойного угла

Рассмотрим несколько примеров использования формул тангенса двойного угла для решения практических задач.

Преобразование тригонометрических выражений

Задача: упростить выражение sin 2α · tg 2α, если известно, что tg α = 0,4:

Решение:

• tg 2α = ^2·0,4/_1−0,16 = 0,8
• sin 2α = 2·sin α·cos α = 2·0,4·0,92 = 0,74
• sin 2α · tg 2α = 0,74·0,8 = 0,592

Вычисление значений тригонометрических функций

Задача: найти значение sin 75°, если известно cos 15° = 0,97:

Решение:

1. 75° = 2·15° + 45°
2. tg (2·15°) = ^{2·tg 15°}/_{1 − tg²15°} = 0,53
3. sin (2·15°) = 0,51
4. cos 45° = 0,71
5. sin 75° = sin(2·15°)·cos 45° + cos(2·15°)·sin 45° = 0,36 + 0,62 = 0,98

Геометрические задачи

В прямоугольном треугольнике с углом α = 25° вычислить длину гипотенузы, если один из катетов равен 5 см.

Решение:

• 2α = 50°
• tg 2α = tg 50° = 1,19 (из таблицы значений)
• tg α = tg 25° = 0,47
• Применяя теорему Пифагора: c² = a² + b² = 5² + c²·tg²α
• Отсюда: c = ^{√25 + 25·tg2α} = ^{√25 + 25·0,22} = 6 см

Применение в технических расчетах

Формулы тангенса двойного и половинного угла широко используются в инженерных расчетах – от проектирования машин и механизмов, до разработки радиотехнических и оптических систем.

• Моделирование колебательных процессов. При анализе гармонических и волновых процессов часто возникает необходимость перехода от функций одинарного аргумента к функциям двойного. Формулы двойного угла позволяют это эффективно осуществить для любых тригонометрических функций, в том числе тангенса.
• Расчеты в строительной механике. При расчете прочности строительных конструкций, таких как балки, фермы и арки, необходим учет углов наклона отдельных элементов. Формулы тангенса удобны для выражения этих углов и вычислений с ними.

Применение в повседневной жизни

Хотя тригонометрия может показаться сугубо теоретической наукой, ее элементы применяются повсеместно в обыденной жизни, иногда даже незаметно для нас.

• Определение расстояний и высот. Используя тангенс угла наклона и известные расстояния или размеры объектов, можно легко определять труднодоступные расстояния или высоты - будь то рост дерева во дворе или высота дальнего здания.
• Навигация и определение местоположения. Многие навигационные приборы, включая GPS, используют тригонометрические функции для расчета координат и определения местоположения. Формулы тангенсов нужны для пересчета углов в прямоугольной системе координат.
• Дизайн и архитектура. Архитекторы и дизайнеры постоянно имеют дело с углами наклона, высотами, пропорциями - будь то разработка конструкций зданий или проектирование интерьеров. Тригонометрические функции в виде тангенсов используются повсеместно.

Автоматизация вычислений

Здесь можно выделить следующие аспекты:

• Инженерные калькуляторы. Специальные инженерные калькуляторы имеют встроенные функции для расчета тригонометрических функций, в том числе тангенса двойного угла. Это позволяет инженерам быстро производить сложные вычисления.
• Математические пакеты. Системы компьютерной математики вроде Matlab и Mathematica имеют мощные средства для работы с тригонометрическими функциями. Любые преобразования, включая двойной аргумент, выполняются автоматически.
• Интернет приложения. В сети существует множество онлайн калькуляторов и инструментов для вычисления тригонометрических функций. Двойной и половинный аргументы поддерживаются в виде стандартных опций.

Перспективы дальнейшего изучения

Несмотря на кажущуюся простоту, тема тангенса двойного угла таит в себе глубокие взаимосвязи, которые можно долго постигать. Кроме классической теории, актуальны такие направления, как:

• Обобщения в рамках комплексных чисел
• Области применения в квантовой физике
• Связи с другими разделами высшей математики