Расстояние до горизонта: удивительные факты о том, как далеко простирается наш взгляд

Когда мы смотрим вдаль, то видим линию горизонта, за которой скрывается остальной мир. Но знаете ли вы, насколько далеко на самом деле простирается наш взгляд? В этой статье мы расскажем об удивительных фактах, связанных с расстоянием до горизонта.

С помощью несложных геометрических формул, основанных на теореме Пифагора, можно с высокой точностью вычислить это расстояние для наблюдателя на Земле. Оказывается, оно напрямую зависит от высоты точки наблюдения над поверхностью планеты.

Как вычислить расстояние до линии горизонта

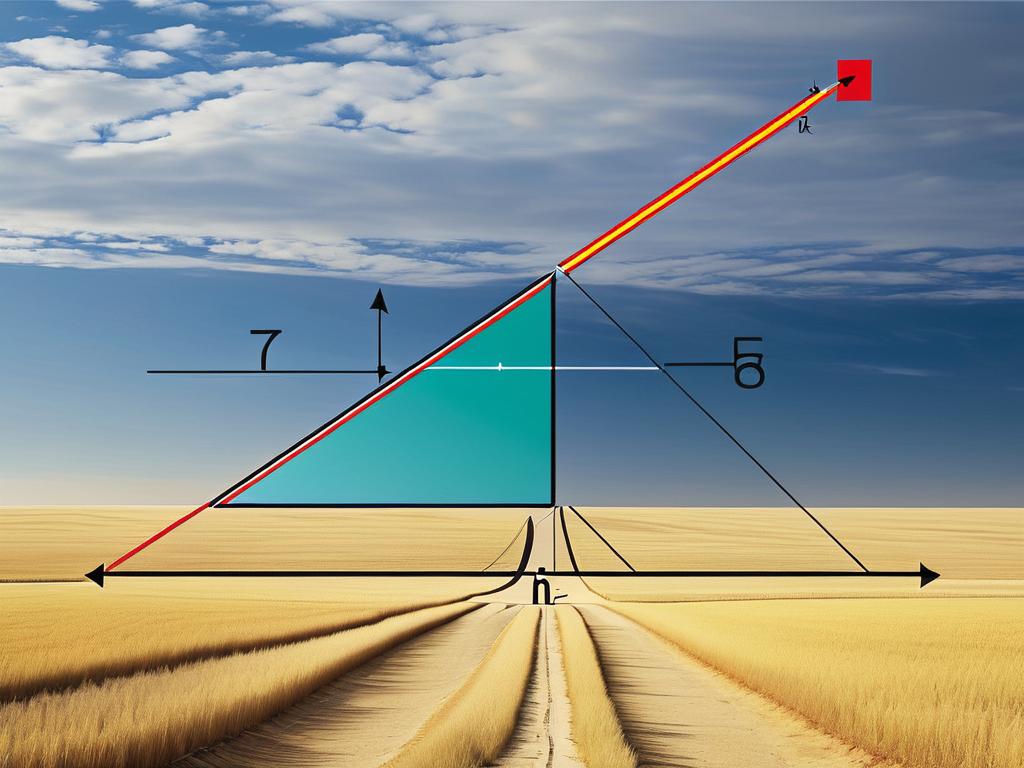
Расстояние до линии горизонта можно вычислить с помощью теоремы Пифагора. Для этого представим Землю в виде шара, а человека, стоящего на ее поверхности, - как продолжение радиуса этого шара. Луч зрения, направленный к горизонту, будет касательной к сфере. Так как касательная перпендикулярна радиусу, то получается прямоугольный треугольник со сторонами:

• радиус Земли R
• высота глаз наблюдателя над поверхностью Земли h
• расстояние до горизонта d

По теореме Пифагора:

Где в качестве R можно взять средний радиус Земли 6370 км. Подставив численные значения радиуса и высоты, получим конкретное расстояние для данного наблюдателя.

Как меняется видимое расстояние при изменении высоты наблюдения

Как видно из приведенной ранее формулы, расстояние до горизонта зависит от радиуса Земли R и высоты глаз наблюдателя над поверхностью h. При фиксированном значении R изменение h влияет на величину расстояния до горизонта.

Чем выше поднимается точка наблюдения, тем дальше отодвигается линия горизонта. Например, стоя на поверхности равнины, человек ростом 1,7 м видит горизонт примерно на 5 км. А если подняться на 20-метровую вышку, горизонт отодвинется уже на 17 км.

Особенностью формулы является то, что с увеличением высоты h расстояние до горизонта d возрастает не прямо пропорционально, а значительно быстрее. Чтобы удвоить d, нужно увеличить h в 4 раза. Это объясняется тем, что в формуле присутствует операция извлечения квадратного корня.

На практике это означает, что на большой высоте горизонт значительно расширяется. Например, с высоты птичьего полета в 10 км открывается уже обзор более чем на 300 км. А с орбиты МКС на высоте 400 км горизонт отодвигается почти на 5000 км!

Конечно, реальная Земля не идеальный шар и имеет рельеф с горами и впадинами. Поэтому расстояние видимости может сильно меняться в зависимости от особенностей ландшафта. Тем не менее, приведенная формула дает хорошее приближенное значение для равнинной местности.

Подытоживая, отметим главное свойство зависимости видимого расстояния от высоты точки наблюдения:

• дальность видимости растет быстрее, чем линейно, при увеличении высоты;
• чтобы значительно увеличить обзор, надо существенно поднять точку обзора.

Интересные примеры расстояний до горизонта в различных условиях

Рассмотрим несколько любопытных примеров, иллюстрирующих как далеко простирается наш взгляд при наблюдении с Земли или околоземного пространства.

На поверхности океана

Моряки, находясь в открытом океане, ограничены видимостью линии горизонта. С палубы корабля или лодки эта дальность составляет около 5 км. Поэтому даже относительно крупные суда за горизонтом скрываются из виду.

Однако благодаря высоте над водой маяки видны гораздо дальше. Например, свет маяка высотой 100 метров заметен за 60 км. А экипаж самолета на высоте 10 км увидит маяк почти за 450 км!

В пустыне Сахара

На обширных песчаных пространствах Сахары особенности рельефа почти отсутствуют. Поэтому формула для вычисления расстояния до горизонта дает хорошее приближение реальной дальности видимости.

Например, для путника ростом 170 см на равнине Сахары открывается вид до 5 км. А вершины гор в этом регионе, достигающие 2000 м и более, видны за 100 км и далее.

С орбиты МКС

Высота орбиты Международной космической станции составляет около 400 км над Землей. Согласно расчетам, с этой высоты горизонт отодвигается почти на 5000 км!

Это позволяет космонавтам на МКС видеть почти весь земной диск. Также они могут наблюдать за погодой на значительной части планеты и движением кораблей в океане.

Конечно, разрешающая способность глаза на таком удалении невелика. Но использование фотокамер позволяет получать достаточно детальные снимки подстилающей поверхности с орбитальной станции.

Практическое применение знаний о дальности видимости в навигации

Знание формулы для расчета расстояния до горизонта и понимание особенностей ее применения имеют большое практическое значение в навигации, особенно морской.

В первую очередь, это позволяет оценить предел видимости на море с палубы корабля или лодки. Как уже говорилось ранее, для наблюдателя высотой около 2 метров он составляет 5-6 км.

Также по формуле можно рассчитать дальность, на которой становится виден маяк или другой высокий ориентир, исходя из его высоты над уровнем моря. Это важно для планирования маршрута судна.

Кроме того, если известна дальность, с которой просматривается маяк, и высота глаз капитана, то по той же формуле можно найти высоту маяка. А зная эту высоту и имея навигационную карту, капитан определяет свое местонахождение.

То есть фактически формула вычисления расстояния до горизонта является важным инструментом в мореплавании, позволяя решать различные навигационные задачи по определению местоположения и прокладыванию курса.

На практике мореплаватели пользуются упрощенным эмпирическим правилом, гласящим, что дальность видимости маяка в морских милях приблизительно равна квадратному корню из его высоты в футах. Но за этим правилом стоит все та же теорема Пифагора и формула вычисления расстояния до горизонта.