Что такое стороны параллелограмма и как их вычислить
Параллелограмм - одна из важнейших фигур в геометрии, которая часто встречается как в теоретических задачах, так и на практике. Знание свойств и формул параллелограмма позволяет эффективно решать многие задачи. В этой статье мы подробно разберем, что представляют собой стороны параллелограмма, каковы их свойства и как можно вычислить сторону, зная другие элементы этой фигуры.
Определение параллелограмма
Параллелограмм – это четырехугольник, у которого противоположные стороны попарно параллельны. В параллелограмме противоположные стороны и попарно параллельные стороны означают, что AB параллельна CD, а AD параллельна BC. Также в параллелограмме выполняется равенство противоположных сторон и противоположных углов.
У параллелограмма есть несколько важных свойств: стороны параллелограмма противоположные равны, сумма соседних углов равна 180°, диагонали пересекаются в точке, которая делит их пополам. Эти свойства позволяют отличать параллелограмм от других четырехугольников и использовать его при решении задач.
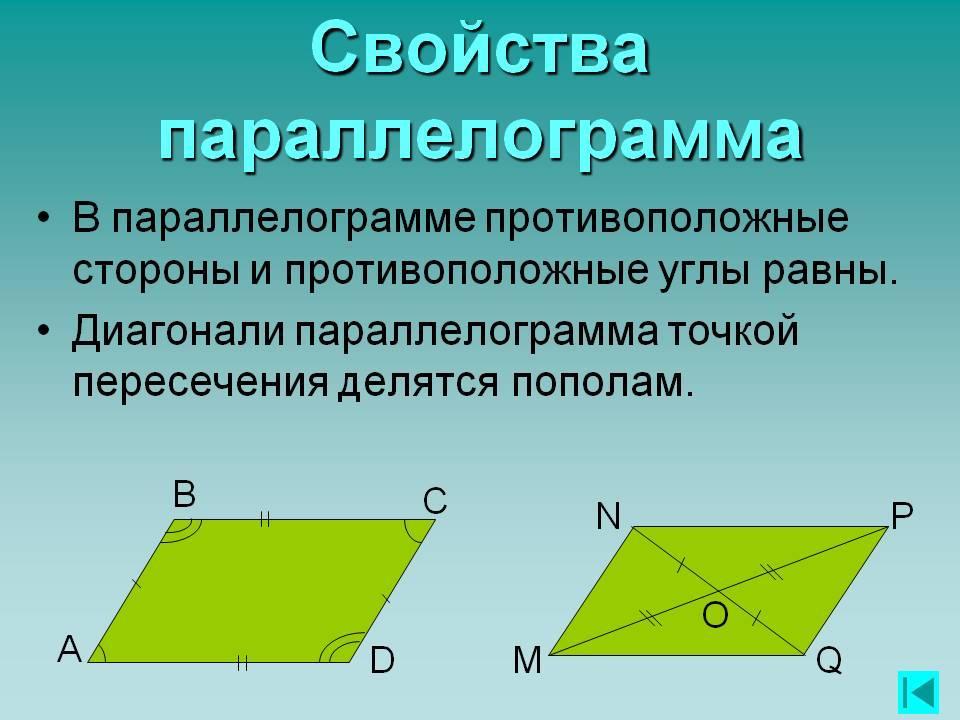
Основные свойства параллелограмма
Согласно определению, у параллелограмма противоположные стороны AB и CD, а также AD и BC попарно равны и параллельны. Из этого следует, что AB = CD и AD = BC.
Другое важное свойство параллелограмма заключается в том, что его диагонали AC и BD пересекаются в некой точке O, причем эта точка делит каждую диагональ пополам: AO = OC и BO = OD.
Из равенства противоположных сторон и свойства диагоналей следует еще один признак параллелограмма - равенство противоположных углов. Углы при вершинах A и C равны, как вертикальные. Также равны углы B и D. Кроме того, в параллелограмме сумма смежных углов равна 180°.
Таким образом, основными отличительными свойствами параллелограмма являются: равенство и параллельность противоположных сторон, равенство противоположных углов, а также деление диагоналей точкой пересечения пополам. Эти свойства позволяют отличить параллелограмм от других четырехугольников и решать задачи, связанные с вычислением его элементов.
Формулы для вычисления сторон параллелограмма
Существует несколько формул, позволяющих вычислить стороны параллелограмма, если известны некоторые его параметры. Рассмотрим основные из них.
- Если известны длины диагоналей параллелограмма d и D, а также одна из его сторон b, то вторая сторона параллелограмма вычисляется по формуле: a = √(D2 + d2 - 2b2)/2, где a - искомая сторона параллелограмма.
- Если известна площадь параллелограмма S и высота h, проведенная к стороне a, то эта сторона вычисляется по формуле: a = S/h.
Кроме того, зная высоту параллелограмма h и противолежащий ей угол α, можно вычислить сторону параллелограмма b по формуле: b = h/sinα. Таким образом, существует несколько способов вычисления сторон параллелограмма в зависимости от известных данных.
| Формула | Условия применения |
| a = √(D2 + d2 - 2b2)/2 | Известны d, D, b |
| a = S/h | Известны S и h |
| b = h/sinα | Известны h и α |
Применение формул на практике
Рассмотрим несколько примеров, демонстрирующих применение рассмотренных выше формул для нахождения сторон.
Задача 1
В параллелограмме ABCD известно, что его диагонали равны AD = 5 см и DB = 4 см. Найти длину стороны AB, если сторона BC равна 3 см.
Решение. Применим формулу: a = √(D2 + d2 - 2b2)/2, где D = 5 см, d = 4 см, b = 3 см. Подставляя значения, получаем: AB = √(25 + 16 - 2*9)/2 = √(32)/2 = 4 см.
Задача 2
Дан параллелограмм ABCD с высотой AH = 10 см, проведенной к стороне AB. Если площадь этого параллелограмма равна 120 см2, найти длину стороны AB.
Решение. Используем формулу для нахождения стороны через площадь и высоту: a = S/h. Подставляя значения, имеем: AB = 120/10 = 12 см.
Задача 3
Один из углов параллелограмма равен 60°. К этому углу проведена высота длиной 5 см. Найти длину противолежащей стороны.
Решение. Применим формулу b = h/sinα, где h = 5 см, α = 60°. Тогда искомая сторона равна: b = 5/sin60° = 5 см.
Как видно из приведенных примеров, для решения задач на вычисление сторон параллелограмма необходимо выбрать подходящую формулу в зависимости от условия задачи и имеющихся данных.