Что такое апофема для многоугольника и пирамиды? Апофема правильной четырехугольной пирамиды

Для успешного решения задач по геометрии необходимо четко понимать термины, которые использует эта наука. Например, таковыми являются "прямая", "плоскость", "многогранник", "пирамида" и многие другие. В данной статье ответим на вопрос, что такое апофема.

Двоякое использование термина "апофема"

В геометрии значение слова "апофема" или "апотема", как ее еще называют, зависит от того, к какому объекту ее применяют. Существует два принципиально разных класса фигур, в которых она является одной из их характеристик.

В первую очередь это плоские многоугольники. Что такое апофема для многоугольника? Это высота, проведенная из геометрического центра фигуры к любой из ее сторон.

Чтобы было понятнее, о чем идет речь, рассмотрим конкретный пример. Предположим, что имеется правильный шестиугольник, показанный ниже на рисунке.

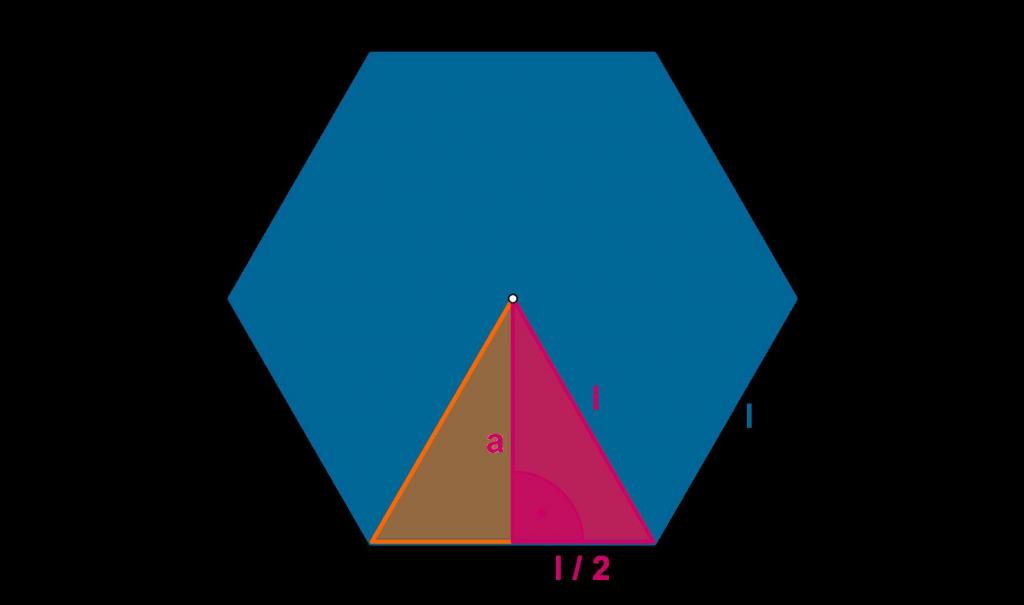
Символом l обозначена длина его стороны, буквой a - апофема. Для отмеченного треугольника она является не только высотой, но и биссектрисой, и медианой. Несложно показать, что через сторону l ее можно вычислить так:

a = √3/2*l

Аналогичным образом апофема определяется для любого n-угольника.

Во вторую очередь - это пирамиды. Что такое апофема для такой фигуры? Этот вопрос требует более детального рассмотрения.

Пирамиды и их апофемы

Для начала дадим определение пирамиде с точки зрения геометрии. Эта фигура представляет собой объемное тело, образованное одним n-угольником (основание) и n треугольниками (боковые стороны). Последние соединены в одной точке, которая называется вершиной. Расстояние от нее до основания - это высота фигуры. Если она попадает на геометрический центр n-угольника, то пирамида называется прямой. Если к тому же n-угольник имеет равные углы и стороны, то фигура называется правильной. Ниже показан пример пирамиды.

Что такое апофема для такой фигуры? Это перпендикуляр, который соединяет стороны n-угольника с вершиной фигуры. Очевидно, что она представляет собой высоту треугольника, являющегося боковой стороной пирамиды.

Апофему удобно использовать при решении геометрических задач с правильными пирамидами. Дело в том, что для них все боковые грани являются равными друг другу равнобедренными треугольниками. Последний факт означает, что все n апофем равны, поэтому для правильной пирамиды можно говорить об одной-единственной такой прямой.

Апофема четырехугольной пирамиды правильной

Пожалуй, самым наглядным примером этой фигуры будет знаменитое первое чудо света - пирамида Хеопса. Она находится в Египте.

Для любой такой фигуры с правильным n-угольным основанием можно привести формулы, позволяющие определить ее апофему через длину a стороны многоугольника, через боковое ребро b и высоту h. Здесь запишем соответствующие формулы для прямой пирамиды с квадратным основанием. Апофема h_b для нее будет равна:

h_b = √(b² - a²/4);

h_b = √(h² + a²/4)

Первое из этих выражений справедливо для любой правильной пирамиды, второе - только для четырехугольной.

Покажем, как эти формулы можно использовать для решения задачи.

Геометрическая задача

Пусть задана прямая пирамида, имеющая квадратное основание. Необходимо рассчитать ее основания площадь. Апофема пирамиды равна 16 см, а ее высота в 2 раза больше стороны основания.

Каждый школьник знает: чтобы найти площадь квадрата, которым является основание рассматриваемой пирамиды, следует знать его сторону a. Для ее нахождения воспользуемся следующей формулой для апофемы:

h_b = √(h² + a²/4)

Значение апофемы известно из условия задачи. Поскольку высота h в два раза больше длины стороны a, это выражение можно преобразовать следующим образом:

h_b = √((2*a)² + a²/4) = a/2*√17 =>

a = 2*h_b/√17

Площадь квадрата равна произведению его сторон. Подставляя полученное выражение для a, имеем:

S = a² = 4/17*h_b²

Остается подставить в формулу значение апофемы из условия задачи и записать ответ: S ≈ 60,2 см².