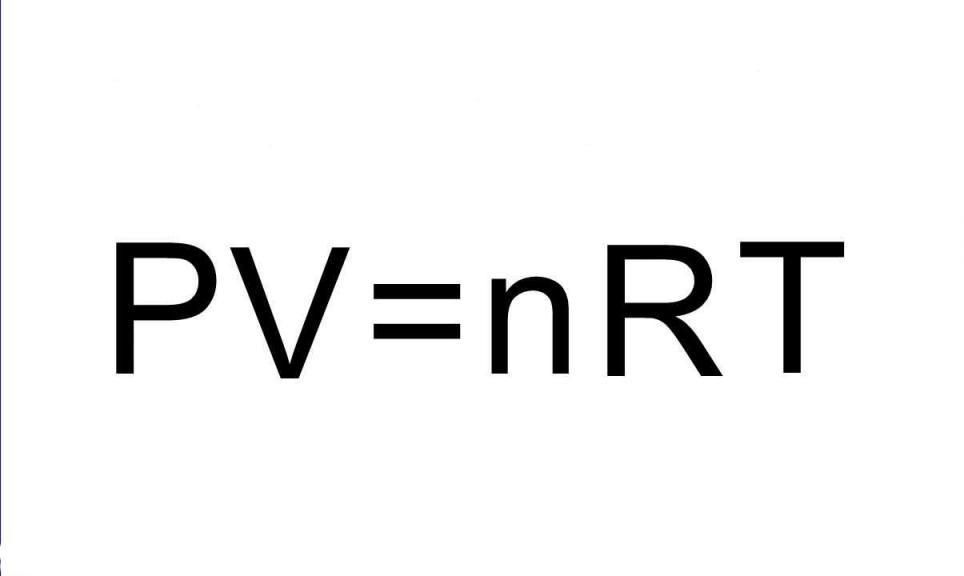Уравнение Менделеева-Клапейрона. Пример задачи
Термодинамика газообразного агрегатного состояния материи - важный раздел физики, который изучает термодинамическое равновесие и квазистатические переходы в системах. Главной моделью, на которой основаны предсказания поведения систем, является модель идеального газа. С ее использованием было получено уравнение Менделеева-Клапейрона. Рассмотрим его в статье.
Идеальный газ

Как известно, все реальные газы состоят из молекул или атомов, расстояния между которыми слишком велики по сравнению с их размерами при невысоких давлениях. Кроме того, при высоких температурах по абсолютной шкале кинетическая энергия молекул превышает их потенциальную энергию, связанную со слабыми диполь-дипольными взаимодействиями (если помимо этих взаимодействий существуют другие виды химической связи, например, ионная или водородная, то они вносят существенный вклад в потенциальную составляющую внутренней энергии системы).
В связи со сказанным, для многих реальных газов при условиях, близких к нормальным, можно пренебречь их внутренними взаимодействиями и размерами частиц. Эти два главных приближения составляют модель идеального газа.
Уравнение Менделеева в физике

Более правильно и справедливо называть это уравнение законом Клапейрона-Менделеева. Дело в том, что впервые записал его французский инженер Эмиль Клапейрон в 1834 году. Сделал он это, анализируя открытые к началу XIX века газовые законы Бойля-Мариотта, Гей-Люссака и Шарля.
Заслуга отечественного химика Дмитрия Менделеева заключается в том, что он придал уравнению современную и удобную в использовании математическую форму. В частности, Менделеев ввел в уравнение постоянную для всех газов R=8,314 Дж/(моль*К). Сам же Клапейрон использовал ряд эмпирических констант, затрудняющих вычислительный процесс.
Уравнение Менделеева-Клапейрона записывается так:
P*V = n*R*T.
Это равенство означает, что произведение давления P на объем V, стоящее в левой части выражения, всегда пропорционально произведению абсолютной температуры T на количество вещества n, находящемуся в левой части.
Изучаемое выражение позволяет получить любой газовый закон, если зафиксировать два из четырех его параметров. В случае изопроцессов, исследуются закрытые системы, в которых обмен с окружающей средой веществом отсутствует (n=const). Эти процессы характеризуются единственным фиксированным термодинамическим параметром (T, P или V).
Пример задачи
Решим теперь задачу на уравнение Менделеева-Клапейрона. Известно, что кислород массой 500 грамм находится в баллоне объемом 100 литров под давлением 2 атмосферы. Чему равна температура в баллоне, если учесть, что система находится в термодинамическом равновесии.
Напомним, что согласно определению, количество вещества вычисляется по формуле:
n = m/M.
Где m - масса всех частиц системы, M - их средняя молярная масса. Это равенство позволяет переписать уравнение Менделеева в такой форме:
P*V = m*R*T/M.
Откуда получаем рабочую формулу для данной задачи:
T = P*V*M/(m*R).
Остается перевести все величины в единицы СИ и подставить их в это выражение:
T = 2*101325*0,1*0,032/(0,5*8,314) = 156 К.
Рассчитанная температура равна -117 oC. Хотя кислород при этой температуре еще является газообразным (конденсируется он при -182,96 oC), в таких условиях модель идеального газа может быть использована только для получения качественной оценки рассчитанной величины.