Определение равных векторов в геометрии: критерии и признаки
При изучении геометрии вводится понятие вектора как направленного отрезка. Чтобы сравнить векторы и производить с ними различные операции, необходимо определение равенства векторов. В данной статье мы разберемся, какие существуют критерии равенства, как это доказать, приведем примеры решения задач.
Для начала дадим определения основных понятий. Рассмотрим свойства равных векторов, сформулируем необходимые и достаточные условия. Затем перейдем к примерам практических задач из школьного курса геометрии.
Определение коллинеарных и равных векторов
Векторы являются важным математическим понятием, широко используемым в физике, инженерных науках и других областях. Чтобы понять, когда два вектора можно считать равными, необходимо ввести понятие коллинеарности.
- Векторы называются коллинеарными, если они лежат на одной прямой или на параллельных прямых.
- Если направления коллинеарных векторов совпадают, то такие векторы называются сонаправленными. В противном случае векторы являются противоположно направленными.
Теперь можно дать определение равных векторов: векторы называются равными, если они сонаправлены и имеют одинаковую длину (модуль). Также для коллинеарных векторов можно говорить об их равенстве, если они имеют одинаковые координаты.
| Свойство | Описание |
| Рефлексивность | Вектор равен самому себе |
| Симметричность | Если вектор а равен вектору b, то и b равен а |
| Транзитивность | Если а=b и b=c, то a=c |
Для равных векторов выполняются перечисленные в таблице свойства. Эти свойства позволяют упростить доказательства в задачах на равенство векторов.
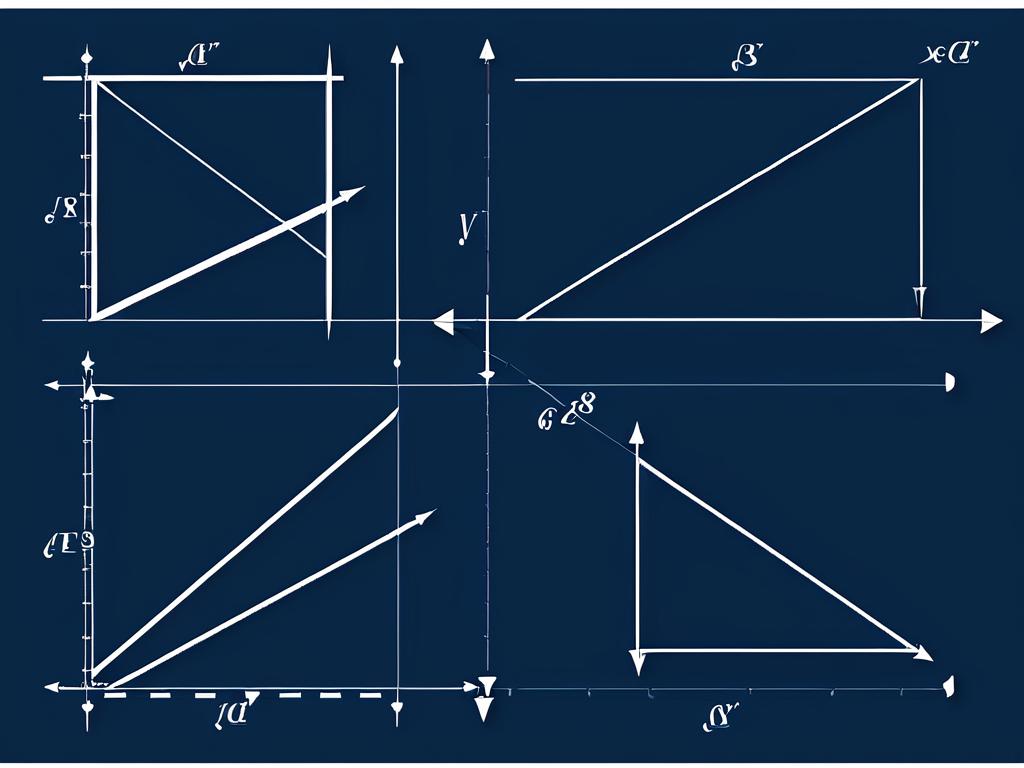
Признаки равенства векторов
Чтобы определить, являются ли два вектора равными, можно воспользоваться следующими основными признаками:
- Векторы имеют одинаковую длину (модуль). Например, если |a| = |b|, то векторы a и b могут быть равны при выполнении второго признака.
- Векторы являются сонаправленными, то есть имеют одинаковое направление.
Для проверки равенства векторов по координатам можно также воспользоваться следующей формулой: если ax = bx, ay = by и az = bz, то векторы a и b равны. Здесь ax, ay, az - координаты вектора a, а bx, by, bz - координаты вектора b.
Стоит отметить, что наличие только одного признака недостаточно для равенства векторов. Например, два вектора могут иметь одинаковую длину, но быть противоположно направленными - в таком случае они не будут считаться равными согласно определению.
Проверка выполнения обоих перечисленных выше признаков является необходимым и достаточным условием для установления равенства двух векторов.
Формулы операций над векторами в геометрии
При решении геометрических задач, связанных с векторами, часто используются различные операции над векторами. Рассмотрим основные из них.
1. Сложение векторов. Если a = (ax, ay) и b = (bx, by) - векторы на плоскости, то их сумма вычисляется по формулам: c = a + b = (ax + bx, ay + by)
2. Вычитание векторов. Разность векторов вычисляется аналогично: c = a - b = (ax - bx, ay - by)
3. Умножение вектора на число. При умножении вектора a = (ax, ay) на число k формулы имеют вид: ka = (k * ax, k * ay)
Зная эти формулы и пользуясь свойствами равенства векторов, можно решать различные геометрические задачи, связанные с доказательством равенства векторов. Например, используя правило транзитивности равенства векторов и формулы сложения, можно доказывать равенство векторных сумм и разностей.
Примеры типовых задач на равенство векторов
Рассмотрим несколько примеров типовых задач на применение свойств равенства векторов из школьного курса геометрии.
Задача 1. Доказать, что векторы a = (3, 4) и b = (-5, -6) не являются равными.
Решение. Найдем длины данных векторов по теореме Пифагора: |a| = 5, |b| = 7. Длины векторов не равны. Кроме того, векторы противоположно направлены. Следовательно, по определению равных векторов, векторы a и b не равны.
Задача 2. Даны три вектора: a = (2, 3), b = (-4, 6), c = (-6, 3). Доказать, что если a = b, то c = a.
Решение. Предположим, что a = b. Тогда по свойству рефлексивности равенства векторов b = a. По свойству транзитивности, если a = b и b = c, то a = c. Значит, из предположения a = b следует, что c = a.
Такие задачи помогают отработать навыки использования определения, признаков и свойств равенства векторов при решении геометрических задач.