Теория вероятностей работает со случайными величинами. Для случайных величин существуют так называемые законы распределения. Такой закон свою случайную величину описывает с абсолютной полнотой. Однако при работе с реальными наборами случайных величин сразу установить закон их распределения часто очень трудно и ограничиваются некоторым набором численных характеристик. Например, вычислить математическое ожидание и дисперсию случайной величины часто бывает очень полезно.
Зачем это нужно
Если суть математического ожидания по смыслу близка к среднему значению величины, то в таком случае дисперсия говорит, как разбросаны значения нашей величины вокруг этого математического ожидания. Например, если мы измеряли IQ у группы людей и хотим исследовать результаты измерений (выборку), математическое ожидание покажет примерное среднее значение коэффициента интеллекта у данной группы людей, а если вычислить дисперсию выборки, мы узнаем, как результаты группируются около математического ожидания: кучкой вблизи него (маленький разброс IQ) или более равномерно на всем участке от минимального до максимального результата (большой разброс, и где-то в середине - мат. ожидание).
Чтобы вычислить дисперсию, необходима новая характеристика случайной величины - отклонение значения от математического ожидания.
Отклонение
Чтобы понять, как вычислять дисперсию, надо сначала разобраться с отклонением. Его определение - разность между значением, которое принимает случайная величина и ее математическим ожиданием. Грубо говоря, для того чтобы понять, как величина "разбрасывается", нужно посмотреть, каким образом распределяется ее отклонение. То есть, мы заменяем значение величины значением ее отклонения от мат. ожидания и исследуем уже его закон распределения.
Закон распределения дискретной, то есть принимающей отдельные значения случайной величины записывается в виде таблицы, где значение величины соотнесено с вероятностью ее появления. Тогда в законе распределения отклонения случайная величина заменится на его формулу, в которой присутствует величина (сохранившая свою вероятность) и ее же мат. ожидание.
Свойства закона распределения отклонения случайной величины
У нас записан закон распределения отклонения случайной величины. Из него мы можем извлечь пока только такую характеристику, как математическое ожидание. Для удобства лучше взять численный пример.
Пусть имеется закон распределения какой-нибудь случайной величины: X - значение, p - вероятность.
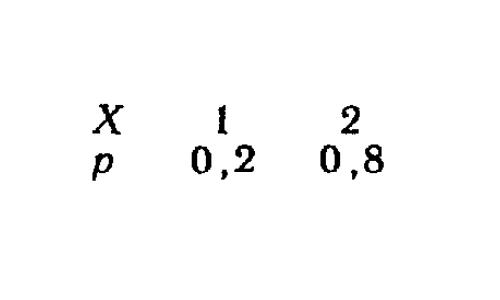
Рассчитываем математическое ожидание по формуле и сразу же отклонения.
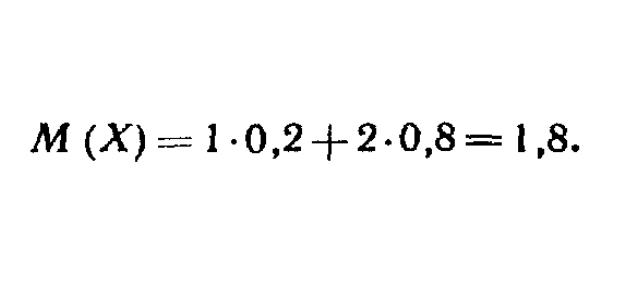
Рисуем новую таблицу распределения отклонения.
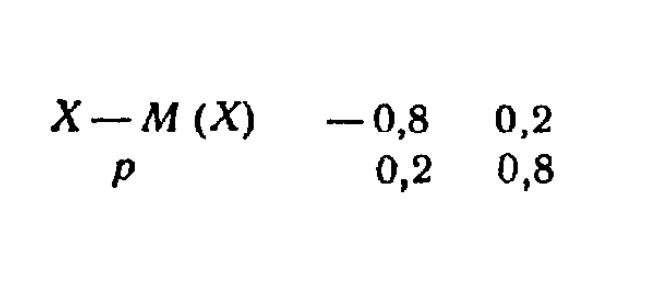
Рассчитываем математическое ожидание и здесь.
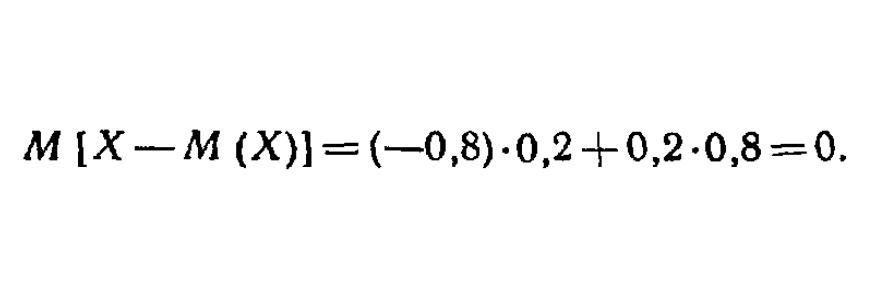
Получается ноль. Пример лишь один, но так будет всегда: это нетрудно доказать в общем случае. Формулу математического ожидания отклонения можно разложить на разность математических ожиданий случайной величины и, как бы ни криво это звучало, математического ожидания мат. ожидания (рекурсия, однако), что есть одно и то же, следовательно, их разность будет равна нулю.
Это ожидаемо: ведь отклонения по знаку бывают как положительными, так и отрицательными, следовательно, в среднем должны давать ноль.
Как вычислять дисперсию дискретной случ. величины
Если мат. ожидание отклонения высчитывать бессмысленно, надо искать что-то другое. Можно просто взять абсолютные значения отклонений (по модулю); но с модулями все не так просто, поэтому отклонения возводят в квадрат, а потом считают их математическое ожидание. Собственно, это и имеется в виду, когда говорят о том, как вычислять дисперсию.
То есть, мы берем отклонения, возводим их в квадрат и составляем таблицу из квадратов отклонений и вероятностей, которые соответствуют случайным величинам. Это новый закон распределения. Чтобы посчитать математическое ожидание, необходимо сложить произведения квадрата отклонения и вероятности.
Более простая формула
Однако началась статья с того, что закон распределения изначальной случайной величины зачастую бывает неизвестен. Поэтому нужно что-то полегче. Действительно, существует другая формула, позволяющая вычислить дисперсию выборки с помощью только мат. ожидания:
Дисперсия - разность между мат. ожиданием квадрата случайной величины и, наоборот, квадратом ее мат. ожидания.
Доказательство этому существует, однако приводить его здесь не имеет смысла, так как оно не имеет практической ценности (а нам-то нужно только посчитать дисперсию).
Как вычислять дисперсию случайной величины в вариационных рядах
В реальной статистике невозможно отразить все случайные величины (потому что их, грубо говоря, как правило, бесконечно много). Поэтому то, что попадает в исследование - так называемая репрезентативная выборка из какой-то общей генеральной совокупности. И, поскольку численные характеристики любой случайной величины из такой генеральной совокупности рассчитываются по выборке, они называются выборочными: выборочное среднее, соответственно, выборочная дисперсия. Вычислить ее можно точно так же, как и обычную (через квадраты отклонений).
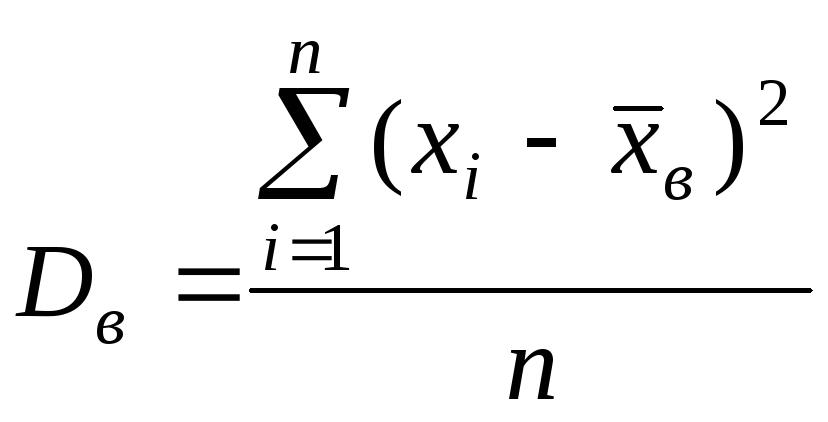
Однако такую дисперсию называют смещенной. Формула несмещенной дисперсии выглядит немного по-другому. Посчитать требуется обычно именно ее.
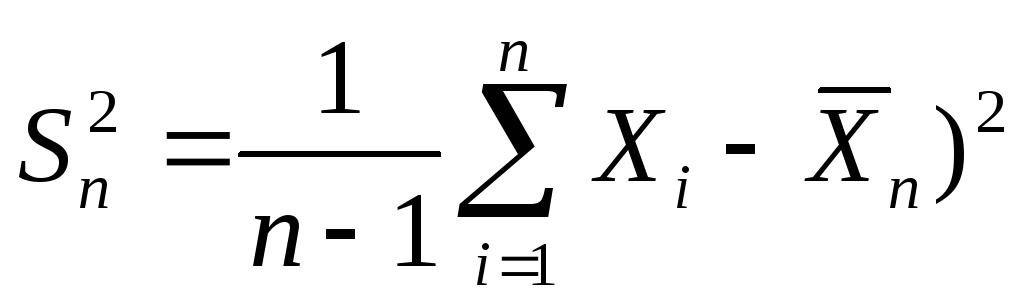
Небольшое дополнение
С дисперсией связана еще одна численная характеристика. Она также служит для оценки того, как рассеивается случайная величина вокруг своего мат. ожидания. В способах, как вычислить дисперсию и среднее квадратическое отклонение нет большой разницы: последнее - это квадратный корень из первого.



























