Какой угол называется центральным углом окружности: определение, свойства, вычисление

Центральные углы окружности - одна из важнейших тем школьного курса геометрии. Знание свойств центральных углов позволяет решать множество геометрических задач, а также применять полученные навыки в реальной жизни. В этой статье мы разберем, что такое центральный угол, изучим его основные свойства и научимся вычислять величину центрального угла и строить его с заданными параметрами.

1. Определение центрального угла окружности

Какой угол называется центральным углом окружности? Центральный угол окружности - это угол, образованный двумя радиусами окружности, выходящими из одной точки - центра окружности. Вершина центрального угла всегда находится в центре окружности. Это одно из ключевых свойств центрального угла.

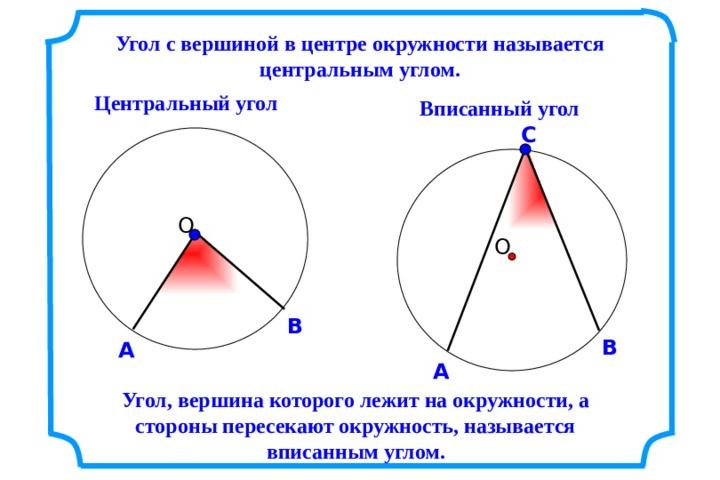
На рисунке изображен центральный угол AOB. Точка O - центр окружности. Лучи OA и OB - радиусы окружности. Угол между ними AOB и есть центральный угол.

Отличие центрального угла от других углов, связанных с окружностью:

• Вершина вписанного угла лежит на окружности.
• Вершина угла, образованного хордой и касательной, лежит вне окружности.

Таким образом, центральный угол - это угол с вершиной строго в центре окружности. Это определяющее свойство центрального угла.

2. Основные свойства центрального угла

Рассмотрим подробнее основные свойства центральных углов:

1. Центральный угол лежит между двумя радиусами одной окружности.
2. Центральный угол равен по величине дуге окружности, на которую он опирается.
3. Центральный угол измеряется в градусах от 0 до 360.
4. Равные центральные углы опираются на равные дуги окружности.
5. Центральный угол в два раза больше вписанного угла, опирающегося на ту же дугу.

Эти свойства позволяют нам решать множество задач, связанных с центральными углами. Например, по величине центрального угла можно найти длину дуги, на которую он опирается, и наоборот.

Центральные углы - мощный инструмент в геометрии, позволяющий связывать углы и дуги окружности.

3. Величина центрального угла окружности

Как уже было сказано ранее, величина центрального угла равна величине дуги, на которую этот угол опирается. Это фундаментальное свойство центрального угла позволяет легко находить его величину.

Рассмотрим основные формулы для вычисления величины центрального угла:

• Центральный угол = Дуге, на которую он опирается
• Центральный угол = 2 * Вписанный угол (опирающийся на ту же дугу)

Давайте рассмотрим несколько примеров применения этих формул.

Пример 1. Дана дуга AB длиной 80°. Найти величину центрального угла AOB.

По формуле 1:

∠AOB = AB = 80°

Пример 2. Дан вписанный угол ABC, равный 40°. Найти центральный угол AOB, опирающийся на ту же дугу.

По формуле 2:

∠AOB = 2 * ∠ABC = 2 * 40° = 80°

Таким образом, зная свойства центральных углов и основные формулы, можно без труда находить их величину в градусах.

4. Построение центрального угла окружности

Давайте теперь разберем, как построить центральный угол окружности с заданными параметрами.

Алгоритм построения центрального угла:

1. Начертить окружность произвольного радиуса.
2. Отметить центр O этой окружности.
3. Из центра O провести два луча под углом, равным заданной величине центрального угла.
4. Угол между этими лучами и есть искомый центральный угол заданной величины.

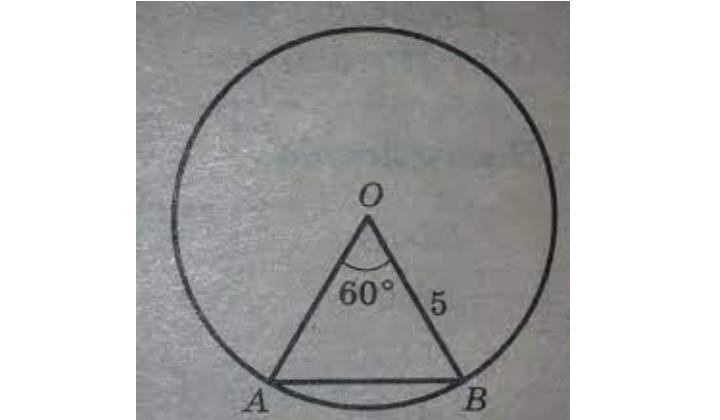
Построим центральный угол в 60°. Сначала проводим окружность и отмечаем ее центр O. Затем из центра проводим два луча под углом 60° друг к другу. Полученный угол AOB и есть центральный угол в 60°.

При построении центральных углов в геометрических редакторах также следует этому алгоритму. Сначала рисуем окружность, затем задаем центральный угол требуемой величины.

Важные моменты при построении центрального угла:

• Точно определить центр окружности O.
• Измерить угол между радиусами с помощью транспортира.
• Лучи проводить аккуратно, чтобы угол получился нужной величины.

Следуя этим рекомендациям, вы без труда научитесь строить центральные углы любой заданной величины.

5. Применение центральных углов окружности

Центральные углы окружности широко применяются для решения разнообразных геометрических задач.

Некоторые примеры применения центральных углов:

• Нахождение длины дуги окружности, если известна величина центрального угла.
• Вычисление величины вписанного угла через центральный.
• Доказательство равенства или подобия треугольников.
• Решение задач на доказательство.

6. Центральный угол в реальной жизни

Хотя центральный угол - это абстрактное геометрическое понятие, его применение можно найти и в реальной жизни.

Например, центральные углы используются в навигации для определения местоположения.

Также они применяются в технических областях - при конструировании машин, механизмов, приборов. Зная свойства центральных углов, инженер может более эффективно спроектировать деталь.

В архитектуре и строительстве центральные углы помогают рассчитать прочность конструкций, нагрузки.

Таким образом, несмотря на кажущуюся абстрактность, центральные углы находят вполне конкретное применение в реальных задачах.

7. Центральный угол в искусстве и дизайне

Центральные углы также применяются в искусстве и дизайне благодаря своим эстетическим свойствам.

Например, центральную композицию часто используют в живописи, фотографии, дизайне интерьеров. Элементы располагаются по радиусам вокруг одного центра, образуя центральные углы.

Архитектурные сооружения также могут иметь центральную симметрию с использованием центральных углов. Это придает им монументальность и завершенность.

В дизайне центральные углы задают гармоничную композицию. Например, лепестки цветка, расходящиеся из одной точки, образуют правильные центральные углы.

Таким образом, центральные углы имеют не только практическое, но и эстетическое значение в искусстве и дизайне.

8. Интересные факты о центральных углах

Рассмотрим несколько любопытных фактов о центральных углах:

• Самый большой центральный угол равен 360° и называется полным углом.
• Центральные углы 90°, 180°, 270° также называются прямыми.
• Два центральных угла, в сумме дающие 360°, называются сверхдополнительными.
• Центральный угол 0° называется нулевым и образуется двумя совпадающими радиусами.
• Центральные углы можно классифицировать на острые, прямые, тупые, в зависимости от их величины.

Знание таких дополнительных фактов о центральных углах расширяет математический кругозор и позволяет лучше запомнить это понятие.

9. Центральный угол в математике

Помимо геометрии, центральные углы имеют приложение и в других областях математики.

Например, в тригонометрии центральные углы используются при изучении синуса, косинуса и тангенса угла.

В математическом анализе центральные углы применяются при исследовании функций и построении графиков в полярной системе координат.

В линейной алгебре центральные углы связаны с понятием ортогональности векторов. Например, векторы, образующие центральный угол 90°, будут ортогональны.

Таким образом, несмотря на кажущуюся простоту, центральные углы окружности имеют глубокий математический смысл и широко применяются в различных областях.

10. Центральный угол - ключевое понятие геометрии

Подводя итог, можно с уверенностью сказать, что центральный угол является одним из ключевых понятий геометрии.

Знание свойств центрального угла, умение вычислять его величину и строить по заданным параметрам - это важнейшие навыки, которыми должен овладеть каждый, кто изучает геометрию.

Центральные углы имеют как практическое применение в технике, строительстве, навигации, так и эстетическое значение в искусстве и дизайне.

Я надеюсь, эта статья помогла вам разобраться, какой угол называется центральным углом окружности и как его применять на практике для решения геометрических задач.

11. Применение центральных углов в физике

Центральные углы окружности также находят применение в физике при решении различных задач.

Например, при равномерном движении по окружности центральный угол, на который повернулось тело, напрямую связан со скоростью и временем движения.

В оптике центральные углы используются при изучении отражения и преломления света на сферических поверхностях.

В электростатике центральный угол между двумя зарядами определяет величину силы их взаимодействия согласно закону Кулона.

Таким образом, несмотря на кажущуюся абстрактность, центральные углы окружности имеют вполне конкретные приложения в физике.

12. Центральный угол в астрономии

Астрономия также активно использует понятие центрального угла.

Например, центральным углом называют угол между направлениями на два светила, вершина которого находится в центре наблюдения.

Центральные углы применяются для определения координат небесных тел, расстояний между ними.

Понятие центрального угла используется в астрономических навигационных системах для вычисления местоположения космических аппаратов.

Таким образом, даже при изучении строения Вселенной в астрономии применяют это фундаментальное понятие геометрии.