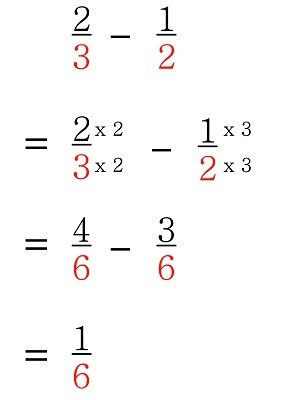Одной из важнейших наук, применение которой можно увидеть в таких дисциплинах, как химия, физика и даже биология, является математика. Изучение этой науки позволяет развить некоторые умственные качества, улучшить абстрактное мышление и способность концентрироваться. Одна из тем, которые заслуживают отдельного внимания в курсе «Математика» - сложение и вычитание дробей. У многих учеников ее изучение вызывает затруднение. Возможно, наша статья поможет лучше понять эту тему.
Как вычесть дроби, знаменатели которых одинаковые
Дроби – это те же числа, с которыми можно производить различные действия. Их отличие от целых чисел заключается в присутствии знаменателя. Именно поэтому при выполнении действий с дробями нужно изучить некоторые их особенности и правила. Наиболее простым случаем является вычитание обыкновенных дробей, знаменатели которых представлены в виде одинакового числа. Выполнить это действие не составит особого труда, если знать простое правило:
- Для того чтобы из одной дроби вычесть вторую, необходимо из числителя уменьшаемой дроби вычесть числитель вычитаемой дроби. Это число записываем в числитель разницы, а знаменатель оставляем тот же: k/m – b/m = (k-b)/m.
Примеры вычитания дробей, знаменатели которых одинаковы
Рассмотрим, как это выглядит на примере:
7/19 - 3/19 = (7 - 3)/19 = 4/19.
От числителя уменьшаемой дроби «7» отнимаем числитель вычитаемой дроби «3», получаем «4». Это число мы записываем в числитель ответа, а в знаменатель ставим то же число, что было в знаменателях первой и второй дроби – «19».
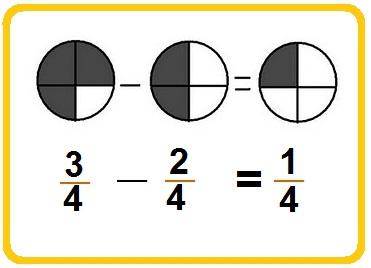
На картинке ниже приведено еще несколько подобных примеров.
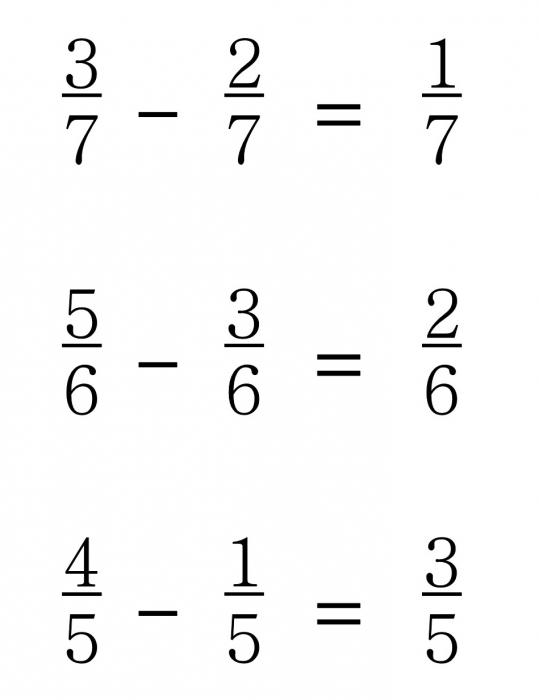
Рассмотрим более сложный пример, где произведено вычитание дробей с одинаковыми знаменателями:
29/47 - 3/47 - 8/47 - 2/47 - 7/47 = (29 - 3 - 8 - 2 - 7)/47 = 9/47.
От числителя уменьшаемой дроби «29» отниманием по очереди числители всех последующих дробей – «3», «8», «2», «7». В итоге получаем результат «9», который записываем в числитель ответа, а в знаменатель записываем то число, которое находится в знаменателях всех этих дробей, - «47».
Сложение дробей, имеющих одинаковый знаменатель
Сложение и вычитание обыкновенных дробей осуществляется по одному и тому же принципу.
- Для того чтобы сложить дроби, знаменатели которых одинаковы, необходимо числители сложить. Полученное число - числитель суммы, а знаменатель останется тот же: k/m + b/m = (k + b)/m.
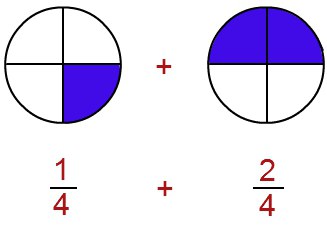
Рассмотрим, как это выглядит на примере:
1/4 + 2/4 = 3/4.
К числителю первой слагаемой дроби - «1» - добавляем числитель второй слагаемой дроби - «2». Результат - «3» - записываем в числитель суммы, а знаменатель оставляем тот же, что присутствовал в дробях, - «4».
Дроби с различными знаменателями и их вычитание
Действие с дробями, которые имеют одинаковый знаменатель, мы уже рассмотрели. Как видим, зная простые правила, решить подобные примеры достаточно легко. Но что делать, если необходимо произвести действие с дробями, которые имеют различные знаменатели? Многие учащиеся средних школ приходят в затруднение перед такими примерами. Но и здесь, если знать принцип решения, примеры уже не будут представлять для вас сложности. Здесь также существует правило, без которого решение подобных дробей просто невозможно.
Чтобы произвести вычитание дробей с разными знаменателями, необходимо их привести к одинаковому наименьшему знаменателю.
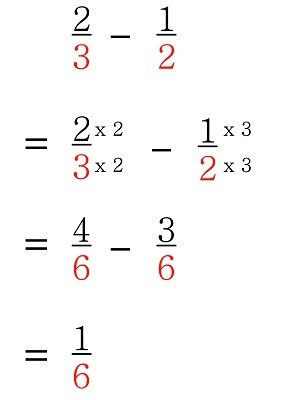
О том, как это сделать, мы поговорим подробнее.
Свойство дроби
Для того чтобы несколько дробей привести к одинаковому знаменателю, нужно использовать в решении главное свойство дроби: после деления или умножения числителя и знаменателя на одинаковое число получится дробь, равная данной.
Так, например, дробь 2/3 может иметь такие знаменатели, как «6», «9», «12» и т. д., то есть она может иметь вид любого числа, которое кратно «3». После того как числитель и знаменатель мы умножим на «2», получится дробь 4/6. После того как числитель и знаменатель исходной дроби мы умножим на «3», получим 6/9, а если аналогичное действие произвести с цифрой «4», получим 8/12. Одним равенством это можно записать так:
2/3 = 4/6 = 6/9 = 8/12…
Как привести несколько дробей к одному и тому же знаменателю
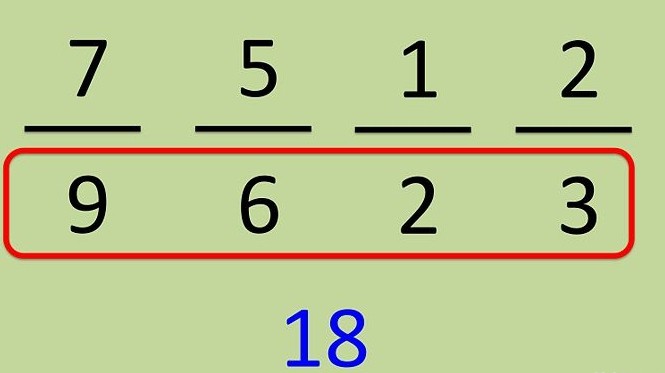
Рассмотрим, как привести несколько дробей к одному и тому же знаменателю. Для примера возьмем дроби, приведенные на картинке ниже. Для начала необходимо определить, какое число может стать знаменателем для их всех. Для облегчения разложим имеющиеся знаменатели на множители.
Знаменатель дроби 1/2 и дроби 2/3 на множители разложить нельзя. Знаменатель 7/9 имеет два множителя 7/9 = 7/(3 х 3), знаменатель дроби 5/6 = 5/(2 х 3). Теперь необходимо определить, какие же множители будут наименьшими для всех этих четырех дробей. Так как в первой дроби в знаменателе имеется число «2», значит, оно должно присутствовать во всех знаменателях, в дроби 7/9 присутствуют две тройки, значит, они также обе должны присутствовать в знаменателе. Учитывая вышесказанное, определяем, что знаменатель состоит из трех множителей: 3, 2, 3 и равен 3 х 2 х 3 = 18.
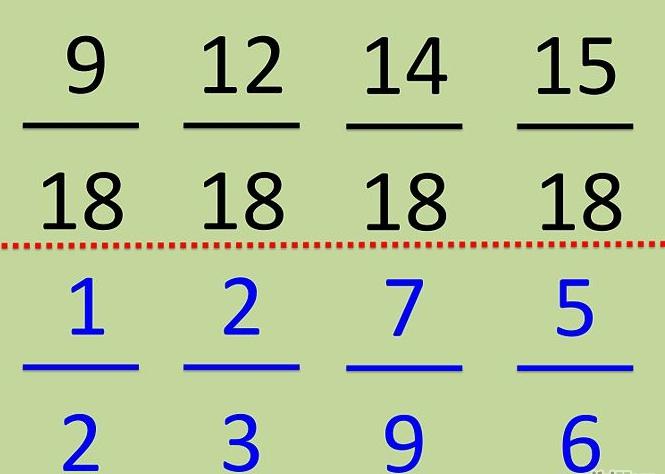
Рассмотрим первую дробь - 1/2. В ее знаменателе имеется «2», но нет ни одной цифры «3», а должно быть две. Для этого мы знаменатель умножаем на две тройки, но, согласно свойству дроби, мы и числитель должны умножить на две тройки:
1/2 = (1 х 3 х 3)/(2 х 3 х 3) = 9/18.
Аналогично производим действия с оставшимися дробями.
- 2/3 – в знаменателе не хватает одной тройки и одной двойки:
2/3 = (2 х 3 х 2)/(3 х 3 х 2) = 12/18. - 7/9 или 7/(3 х 3) – в знаменателе не хватает двойки:
7/9 = (7 х 2)/(9 х 2) = 14/18. - 5/6 или 5/(2 х 3) – в знаменателе не хватает тройки:
5/6 = (5 х 3)/(6 х 3) = 15/18.
Все вместе это выглядит так:
Как вычесть и сложить дроби, имеющие различные знаменатели
Как уже говорилось выше, для того чтобы произвести сложение или вычитание дробей, имеющих различные знаменатели, их необходимо привести к одному знаменателю, а дальше воспользоваться правилами вычитания дробей, имеющих одинаковый знаменатель, о котором уже рассказывалось.
Рассмотрим это на примере: 4/18 – 3/15.
Находим кратное чисел 18 и 15:
- Число 18 состоит из 3 х 2 х 3.
- Число 15 состоит из 5 х 3.
- Общее кратное будет состоять из следующих множителей 5 х 3 х 3 х 2 = 90.
После того как знаменатель будет найден, необходимо вычислить множитель, который будет отличным для каждой дроби, то есть то число, на которое необходимо будет умножить не только знаменатель, но и числитель. Для этого число, которое мы нашли (общее кратное), делим на знаменатель той дроби, у которой нужно определить дополнительные множители.
- 90 поделить на 15. Полученное число «6» будет множителем для 3/15.
- 90 поделить на 18. Полученное число «5» будет множителем для 4/18.
Следующий этап нашего решения – приведение каждой дроби к знаменателю «90».
Как это делается, мы уже говорили. Рассмотрим, как это записывается в примере:
(4 х 5)/(18 х 5) – (3 х 6)/(15 х 6) = 20/90 – 18/90 = 2/90 = 1/45.
Если дроби с маленькими числами, то можно общий знаменатель определить, как в примере, приведенном на картинке ниже.
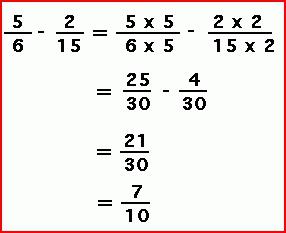
Аналогично производится и сложение дробей, имеющих различные знаменатели.
Вычитание и сложение дробей, имеющих целые части
Вычитание дробей и их сложение мы уже детально разобрали. Но как произвести вычитание, если у дроби есть целая часть? Опять же, воспользуемся несколькими правилами:
- Все дроби, имеющие целую часть, перевести в неправильные. Говоря простыми словами, убрать целую часть. Для этого число целой части умножаем на знаменатель дроби, полученное произведение добавляем к числителю. То число, которое получится после этих действий, – числитель неправильной дроби. Знаменатель же остается неизменным.
- Если дроби имеют различные знаменатели, следует привести их к одинаковому.
- Произвести сложение или вычитание с одинаковыми знаменателями.
- При получении неправильной дроби выделить целую часть.
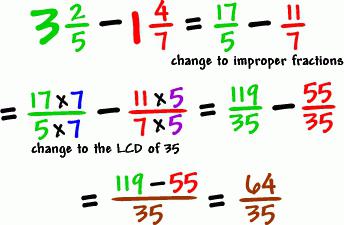
Есть и иной способ, при помощи которого можно осуществить сложение и вычитание дробей с целыми частями. Для этого производятся отдельно действия с целыми частями, и отдельно действия с дробями, а результаты записываются вместе.
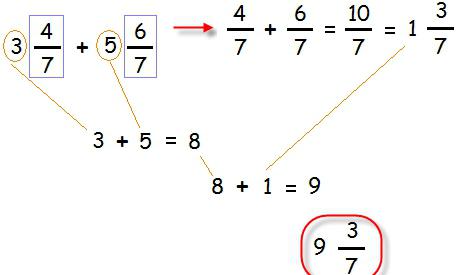
Приведенный пример состоит из дробей, которые имеют одинаковый знаменатель. В том случае, когда знаменатели различны, их необходимо привести к одинаковому, а далее выполнить действия, как показано на примере.
Вычитание дробей из целого числа
Еще одной из разновидностей действий с дробями является тот случай, когда дробь необходимо отнять от натурального числа. На первый взгляд подобный пример кажется трудно решаемым. Однако здесь все довольно просто. Для его решения необходимо перевести целое число в дробь, причем с таким знаменателем, который имеется в вычитаемой дроби. Далее производим вычитание, аналогичное вычитанию с одинаковыми знаменателями. На примере это выглядит так:
7 - 4/9 = (7 х 9)/9 - 4/9 = 53/9 - 4/9 = 49/9.
Приведенное в этой статье вычитание дробей (6 класс) является основой для решения более сложных примеров, которые рассматриваются в последующих классах. Знания этой темы используются впоследствии для решения функций, производных и так далее. Поэтому очень важно разобраться и понять действия с дробями, рассматриваемые выше.