Критерий Гурвица. Критерии устойчивости Вальда, Гурвица, Сэвиджа
В статье рассмотрены такие понятия, как критерии Гурвица, Сэвиджа и Вальда. Упор сделан преимущественно на первый. Критерий Гурвица подробно описан как с алгебраической точки зрения, так и с позиции принятия решения в условиях неопределенности.
Стоит начать с определения понятия устойчивости. Оно характеризует способность системы возвращаться к равновесному состоянию по окончании возмущения, которое нарушило сформировавшееся ранее равновесие.
Важно отметить, что его оппонент - неустойчивая система - постоянно удаляется от своего равновесного состояния (совершает колебания вокруг него) с возвращающей амплитудой.
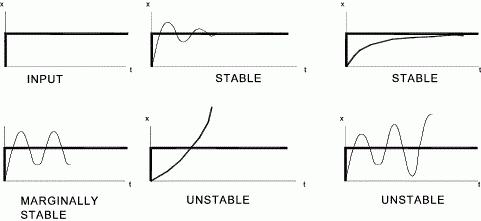
Критерии устойчивости: определение, виды
Это свод правил, которые позволяют судить о существующих знаках корней характеристического уравнения без поиска его решения. А последние, в свою очередь, предоставляют возможность судить об устойчивости конкретной системы.
Как правило, они бывают:
- алгебраическими (составление по конкретному характеристическому уравнению алгебраических выражений с применением специальных правил, которые характеризуют устойчивость САУ);
- частотными (объект изучения - частотные характеристики).
Критерий устойчивости Гурвица с алгебраической точки зрения
Им выступает алгебраический критерий, подразумевающий рассмотрение определенного характеристического уравнения в виде стандартной формы:
A(p)=aᵥpᵛ+aᵥ₋₁pᵛ¯¹+…+a₁p+a₀=0.
Посредством его коэффициентов формируется матрица Гурвица.

Правило составления матрицы Гурвица
В направлении сверху вниз по порядку выписываются все коэффициенты соответствующего характеристического уравнения, начиная от aᵥ₋₁ до a0. Во всех столбцах вниз от главной диагонали указывают коэффициенты возрастающих степеней оператора p, затем вверх – убывающих. Недостающие элементы заменяются нулями.
Принято считать, что система устойчива, когда все имеющиеся диагональные миноры рассматриваемой матрицы положительны. Если главный определитель равен нулю, то можно говорить о нахождении ее на границе устойчивости, причем аᵥ=0. В случае соблюдения остальных условий рассматриваемая система располагается на границе новой апериодической устойчивости (предпоследний минор приравнивается к нулю). При положительном значении оставшихся миноров – на границе уже колебательной устойчивости.
Принятие решения в ситуации неопределенности: критерии Вальда, Гурвица, Сэвиджа
Они являются критериями выбора наиболее целесообразной вариации стратегии. Критерий Сэвиджа (Гурвица, Вальда) применяется в ситуации, когда имеют место неопределенные априорные вероятности состояний природы. Их основа – анализ матрицы рисков либо платежной матрицы. В случае неизвестности распределения вероятностей будущих состояний вся имеющаяся информация сводится к списку ее возможных вариантов.
Итак, стоит начать с максиминного критерия Вальда. Он выступает критерием крайнего пессимизма (осторожного наблюдателя). Данный критерий можно сформировать и для чистых, и для смешанных стратегий.
Свое название он получил на основании предположения статиста касательно того, что природа может реализовать состояния, в рамках которых величина выигрыша приравнена к наименьшему значению.
Этот критерий тождественен пессимистическому, который применяется в ходе решения матричных игр, чаще всего в чистых стратегиях. Так, сначала необходимо выбрать из каждой строки минимальное значение элемента. Затем выделяется стратегия ЛПР, которая соответствует максимальному элементу среди уже отобранных минимальных.
Выбранные посредством рассматриваемого критерия варианты лишены риска, так как ЛПР не сталкивается с более плохим результатом, чем тот, который выступает ориентиром.
Итак, самой приемлемой, согласно критерию Вальда, признана чистая стратегия, так как она в худших условиях гарантирует максимально предельный выигрыш.
Далее стоит рассмотреть критерий Сэвиджа. Здесь при выборе 1-го из доступных решений на практике, как правило, останавливаются на таком, который приведет к минимальным последствиям в случае, если выбор все же окажется ошибочным.
Согласно данному принципу, всякое решение характеризуется некой величиной дополнительных потерь, возникающих в ходе его осуществления, по сравнению с правильным при имеющимся состоянии природы. Очевидно, что правильное решение не может нести дополнительные потери, ввиду чего их величина приравнена к нулю. Так, в роли наиболее целесообразной принимается стратегия, величина потерь в которой минимальна при худшем стечении обстоятельства.
Критерий пессимизма-оптимизма
Так по-другому называется критерий Гурвица. В процессе выбора решения, в ходе оценки сложившейся ситуации вместо двух крайностей придерживаются так называемой промежуточной позиции, которая учитывает вероятность как благоприятного, так и наихудшего поведения природы.
Данный компромиссный вариант предложил Гурвиц. Согласно ему, для всякого решения понадобится установить линейную комбинацию min и max, далее выбрать стратегию, которая соответствует их наибольшему значению.
Когда оправдано применение рассматриваемого критерия?
Использовать критерий Гурвица целесообразно в ситуации, характеризующейся следующими признаками:
- Существует необходимость взятия во внимание наихудшего из вариантов.
- Отсутствие знаний касательно вероятностей состояний природы.
- Допустим некоторый риск.
- Реализуется достаточно малое число решений.
Заключение
Напоследок будет нелишне напомнить, что в статье были рассмотрены критерии Гурвица, Сэвиджа и Вальда. Критерий Гурвица подробно описан с различных точек зрения.