Существует несколько основных алгоритмов решения задачи сортировки массива. Один из самых известных среди них - сортировка вставками. В силу своей наглядности и простоты, но малой эффективности, этот метод используется в основном при обучении программированию. Он позволяет разобраться в основных механизмах сортировки.
Описание алгоритма
Суть алгоритма сортировки вставками заключается в том, что внутри исходного массива формируется упорядоченный нужным образом сегмент. Каждый элемент по одному сравнивается с проверенной частью и вставляется на положенное место. Таким образом, после перебора всех элементов они выстраиваются в правильном порядке.
Очередность выбора элементов может быть любой, они могут отбираться произвольно или согласно некоему алгоритму. Чаще всего используется последовательный перебор с начала массива, где и формируется упорядоченный сегмент.
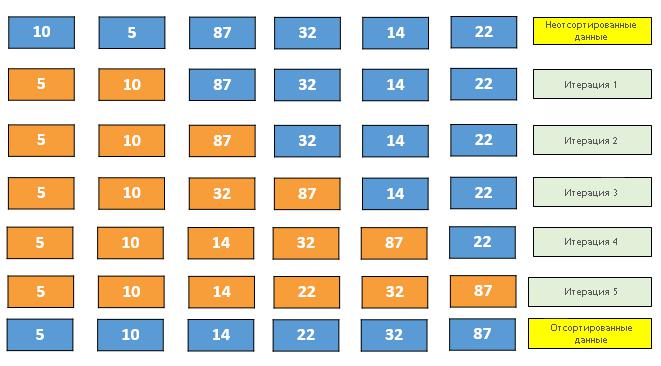
Начало сортировки может выглядеть следующим образом:
- Взять первый элемент массива.
- Так как его не с чем сравнивать, принять сам элемент за упорядоченную последовательность.
- Перейти ко второму элементу.
- Сравнить его с первым, исходя из правила сортировки.
- При необходимости поменять элементы местами.
- Принять два первых элемента за упорядоченную последовательность.
- Перейти к третьему элементу.
- Сравнить его со вторым, при необходимости поменять местами.
- Если замена произведена, сравнить его с первым.
- Принять три элемента за упорядоченную последовательность.
И так далее до конца исходного массива.
Сортировка вставками в реальной жизни
Для наглядности стоит привести пример того, как используется этот механизм сортировки в обычной жизни.
Возьмем, например, кошелек. В отделении для банкнот лежат в беспорядке сотенные, пятисотенные и тысячные купюры. Это непорядок, в такой мешанине сложно сразу найти нужную бумажку. Массив купюр необходимо отсортировать.
Самой первой идет банкнота номиналом в 1000 рублей, а сразу за ней - 100. Берем сотенную и размещаем ее впереди. Третья по счету - 500 рублей, законное место для нее - между сотней и тысячей.
Таким же образом мы сортируем полученные карты при игре в "Дурака", чтобы было проще ориентироваться в них.

Операторы и вспомогательные функции
Метод сортировки вставками принимает на вход исходный массив, который следует упорядочить, функцию сравнения и при необходимости функцию, определяющую правило перебора элементов. Чаще всего вместо нее используется обычный оператор цикла.
Первый элемент сам по себе является упорядоченным множеством, поэтому сравнение начинается со второго.
В алгоритме часто применяется вспомогательная функция для обмена двух значений (swap). Она использует дополнительную временную переменную, что требует затрат памяти и немного замедляет работу кода.
Альтернативой является массовое смещение группы элементов и последующая вставка текущего на освободившееся место. При этом переход к следующему элементу происходит тогда, когда сравнение выдало положительный результат, что свидетельствует о правильном порядке.

Примеры реализации
Конкретная реализация во многом зависит от используемого языка программирования, его синтаксиса и структур.
Классическая реализация на языке C с использованием временной переменной для обмена значений:
int i, j, temp;
for (i = 1; i < size; i++)
{
temp = array[i];
for (j = i - 1; j >= 0; j--)
{
if (array[j] < temp)
break;
array[j + 1] = array[j];
array[j] = temp;
}
}Реализация на PHP:
function insertion_sort(&$a) {
for ($i = 1; $i < count($a); $i++) {
$x = $a[$i];
for ($j = $i - 1; $j >= 0 && $a[$j] > $x; $j--) {
$a[$j + 1] = $a[$j];
}
$a[$j + 1] = $x;
}
}Здесь сначала происходит смещение вправо всех элементов, несоответствующих условию сортировки, а затем текущий элемент вставляется на освободившееся место.
Код Java с использованием цикла while:
public static void insertionSort(int[] arr) {
for(int i = 1; i < arr.length; i++){
int currElem = arr[i];
int prevKey = i - 1;
while(prevKey >= 0 && arr[prevKey] > currElem){
arr[prevKey+1] = arr[prevKey];
arr[prevKey] = currElem;
prevKey--;
}
}
}Общий смысл кода остается неизменным: каждый элемент массива последовательно сравнивается с предыдущими и меняется с ними местами при необходимости.
Оценка времени работы
Очевидно, что в самом лучшем случае на входе алгоритма будет уже упорядоченный правильным образом массив. В этой ситуации алгоритму придется просто проверить каждый элемент, чтобы убедиться, что он стоит на своем месте, не осуществляя обменов. Таким образом, время работы будет напрямую зависеть от длины исходного массива O(n).
Худший случай входных данных - массив, отсортированный в порядке, обратном нужному. Здесь потребуется большое количество перестановок, функция времени выполнения будет зависеть от количества элементов, возведенного в квадрат.
Точное количество перестановок для абсолютно неупорядоченного массива можно вычислить по формуле:
n*(n-1)/2, где n - длина исходного массива. Таким образом, для расстановки 100 элементов в правильном порядке потребуется 4950 перестановок.
Метод вставок весьма эффективен для сортировки небольших или частично упорядоченных массивов. Однако повсеместно применять его не рекомендуется из-за высокой сложности вычислений.
Алгоритм используется как вспомогательный во многих других более сложных методах сортировки.
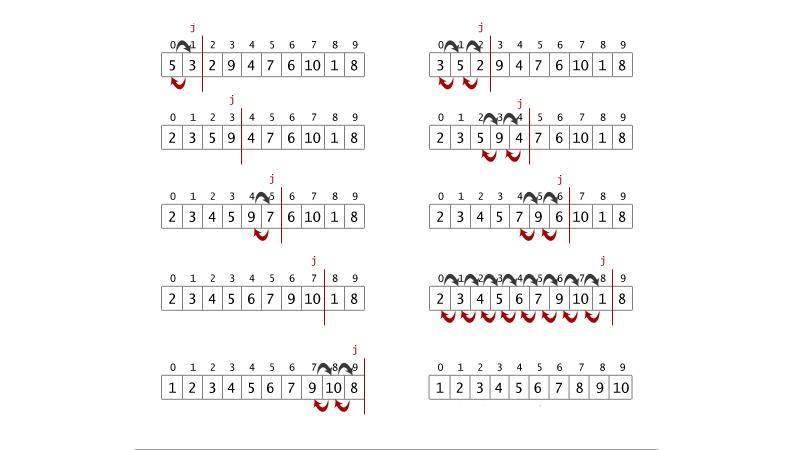
Сортировка одинаковых значений
Алгоритм вставок относится к так называемым устойчивым сортировкам. Это означает, что он не меняет местами одинаковые элементы, а сохраняет их исходный порядок. Показатель устойчивости во многих случаях важен для правильного упорядочивания.

Выше представлен великолепный наглядный пример сортировки вставками в танце.


























