Диагонали являются важным структурным элементом призмы. Знание их свойств и особенностей помогает при решении многих задач стереометрии. Давайте подробно разберемся с тем, что представляют собой диагонали, как их вычислять и для чего они нужны.
Основные понятия о призме
Прежде чем перейти непосредственно к диагоналям призмы, давайте напомним, что из себя представляет сама призма.
Призмой называется многогранник, составленный из двух равных многоугольников, лежащих в параллельных плоскостях и соединенных боковыми гранями-параллелограммами.
Основными элементами призмы являются:
- Основания - два равных многоугольника
- Боковые грани - параллелограммы, соединяющие основания
- Высота - перпендикуляр между плоскостями оснований
- Боковые ребра - общие стороны боковых граней
- Диагональ - отрезок между двумя вершинами из разных оснований
Различают прямые и наклонные призмы. У прямых боковые ребра перпендикулярны плоскостям оснований. Прямые призмы с правильными многоугольниками в основании называются правильными.
Для вычислений объема и площади поверхности призмы используются следующие формулы:
| Объем призмы | V = S основания * H |
| Площадь полной поверхности | S полн = S боковой поверхности + 2*S основания |
| Площадь боковой поверхности прямой призмы | S бок = P основания * H |
Существуют призмы с треугольными, четырехугольными и другими основаниями. Наиболее распространены прямоугольные призмы, у которых основанием служит прямоугольник. Частным случаем прямоугольной призмы является известный нам куб.

Что такое диагонали призмы
Диагонали призмы - это отрезки, соединяющие несмежные вершины призмы. Различают два типа диагоналей:
- Диагонали граней
- Внутренние диагонали
Первые соединяют несоседние вершины в плоскости грани призмы, будь то основание или боковая грань. Их длину можно найти из размеров соответствующей грани.
Вторые проходят внутри объема призмы между вершинами разных оснований. Для их вычисления нужно знать параметры оснований и боковых ребер фигуры. Эти диагонали особенно важны при решении задач на комбинации тел.
У диагонали правильной призмы есть интересная особенность: из-за симметрии фигуры все такие диагонали равны между собой. Это сильно упрощает многие вычисления с правильными призмами.
На этом мы завершаем краткий обзор основ теории призм и переходим непосредственно к диагоналям.
Вычисление длины диагоналей
Для нахождения длины диагонали призмы используется несколько подходов в зависимости от типа самой призмы и расположения диагонали.
Общий подход к вычислению диагоналей
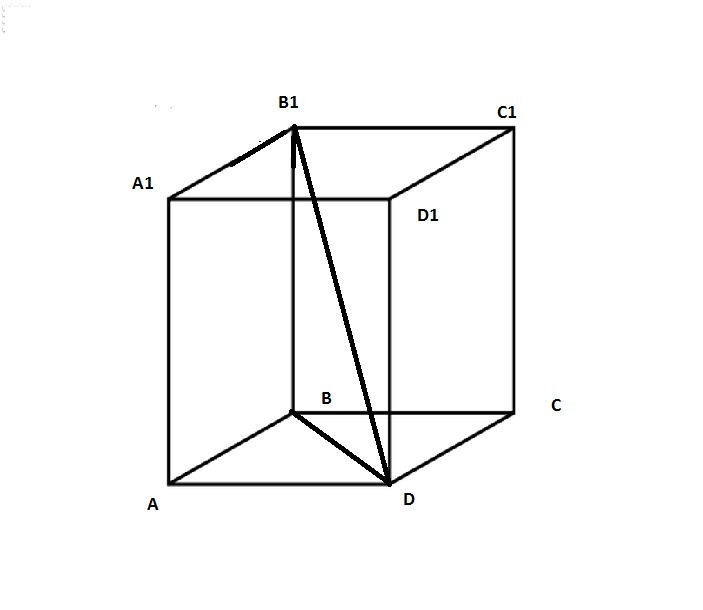
В общем случае диагональ представляет собой гипотенузу некоторого прямоугольного треугольника. Для вычисления ее длины применяют теорему Пифагора:
Здесь c - искомая диагональ, а a и b - составляющие, образующие с ней прямоугольный треугольник.
Использование тригонометрических функций
В случае правильной или наклонной призмы для вычислений диагоналей часто используют тригонометрические функции. Например, формула для диагонали правильной пятиугольной призмы имеет вид:
Здесь a - сторона основания, h - высота призмы, а α - угол при вершине правильного пятиугольника равный 108°.
Формулы для прямой призмы
Для прямой призмы с прямоугольным основанием есть простая формула длины диагонали через основание a, b и высоту h:
А для диагонали грани параллелограмма используется теорема Пифагора для прямоугольного треугольника, образованного сторонами параллелограмма a, b и диагональю d:
Формулы для правильной призмы
Уже упомянутая формула для диагонали правильной пятиугольной призмы. А вот общая формула для любой правильной n-угольной призмы:
Здесь a - сторона правильного n-угольника, h - высота призмы, α - угол при вершине правильного n-угольника.
Примеры конкретных вычислений
Рассмотрим на конкретных числовых примерах, как можно вычислить длину различных диагоналей призмы.
Пусть дана прямая четырехугольная призма со стороной основания 6 см и высотой 8 см. Найдем длину:
- Диагонали основания
- Диагонали бокового прямоугольника
- Внутренней диагонали между основаниями
Для диагонали квадратного основания со стороной 6 см получаем по теореме Пифагора: d1 = √(62 + 62) = √72 = 8,5 см
Диагональ b бокового прямоугольника со сторонами 6 и 8 см: d2 = √(62 + 82) = √100 = 10 см
Внутренняя диагональ с использованием формулы для прямой призмы: d3 = √(82 + 62) = √136 = 11,7 см
Рекомендации по решению сложных задач на вычисление диагоналей
При решении задач повышенной сложности, связанных с вычислением длин диагоналей призм, рекомендуется использовать следующий алгоритм:
- Определить тип призмы и ее параметры
- Выбрать подходящую формулу в зависимости от вида диагонали и характеристик призмы
- При необходимости разбить призму на более простые фигуры
- Составить систему уравнений из известных данных и искомых параметров
- Решить полученную систему уравнений
Следуя такому плану, можно разобраться практически с любой задачей на диагонали призмы.























