Тригонометрия - фундамент математических наук, без которого невозможно представить современную цивилизацию. Эта статья раскроет суть тригонометрии и ее вклад в развитие человечества.
История возникновения тригонометрии
Тригонометрия это наука о тригонометрических функциях, чье название впервые появилось в книге Бартоломеуса Питискуса в 1595 году. Однако сама наука зародилась гораздо раньше, еще в Древней Греции, когда ученые столкнулись с необходимостью решать задачи геометрии и астрономии.
Первые тригонометрические таблицы были составлены Гиппархом Никейским (180-125 гг. до н.э.). Он первым свел в таблицы значения дуг и хорд для различных углов. Позднее это учение о хордах развил Клавдий Птолемей (90-168 гг н.э.) в своем труде "Альмагест".
В Средневековой Индии произошел переход от хорд к синусам. Это позволило ввести различные тригонометрические функции и заложило основы тригонометрии как науки о тригонометрических величинах. Индийские ученые составляли подробные таблицы значений этих функций, необходимые для астрономических вычислений.
В 8-15 веках тригонометрию активно развивали ученые арабского мира, а затем их достижения были переняты европейской наукой. Так тригонометрия приобрела современный вид.
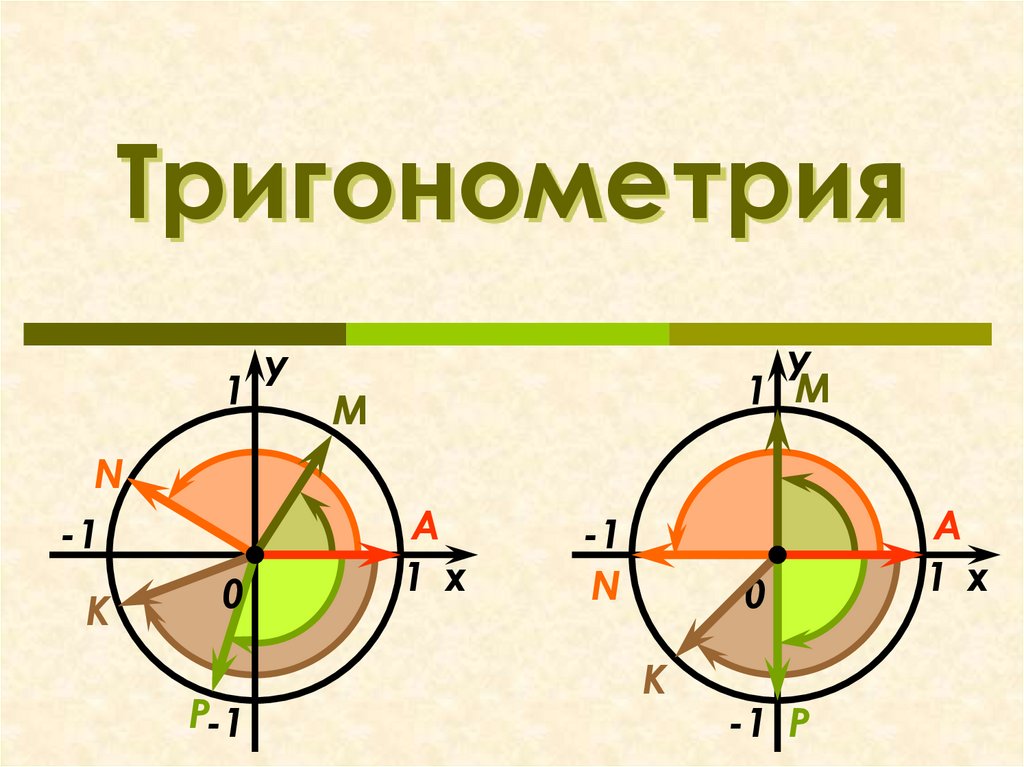
Основные понятия и определения тригонометрии
Ключевыми объектами изучения тригонометрии являются тригонометрические функции - синус, косинус, тангенс и котангенс. Эти функции выражают зависимость между сторонами и углами прямоугольного треугольника.
Тригонометрия (от греческого "тригонон" - треугольник) буквально означает " измерение треугольников ". Именно для этого тригонометрические функции и применяются в геометрии, а также в физике, астрономии и других областях.
Определения тригонометрических функций для острых углов (от 0 до 90 градусов) были даны еще в Древней Греции. В 18 веке Леонард Эйлер расширил эти определения на всю числовую ось, что позволило применять тригонометрию в более общем виде.
Помимо определений, в тригонометрии существует множество формул и тождеств, выражающих связи между функциями. Например, тождества для синуса и косинуса суммы и разности углов были известны еще в Древней Греции как "теорема о делении хорд" . Эти формулы лежат в основе многих тригонометрических вычислений.
Области применения тригонометрии
Благодаря универсальности тригонометрических функций, эта наука находит самое широкое применение в самых разных сферах человеческой деятельности.
- Инженерные расчеты в строительстве, машиностроении, энергетике
- Навигация морских и воздушных судов, геодезия
- Физические эксперименты и теоретические исследования
- Экономика и финансы
- Архитектура

Этот список можно продолжать очень долго. Практически в любой работе по тригонометрии - будь то инженерные расчеты конструкций или исследования в области фундаментальной физики - используются тригонометрические функции и формулы.
Даже в таких, казалось бы, далеких от математики областях как музыка или фонетика, тригонометрия играет важную роль. Она позволяет описывать и анализировать звуковые колебания, лежащие в основе этих дисциплин.
Одним из ярких примеров прикладного использования тригонометрии является техника триангуляции. Она широко применяется в геодезии, навигации, картографии и позволяет определять неизвестные расстояния и координаты по известным параметрам треугольников. Например, расстояния до звезд в астрономии или между географическими объектами на Земле.
Тригонометрия и компьютерные технологии
В наши дни тригонометрия активно используется в сфере информационных технологий. Компьютерные методы позволяют быстро и точно проводить сложные тригонометрические расчеты, которые раньше требовали огромных затрат времени и сил.
Тригонометрические функции лежат в основе таких важнейших областей программирования и компьютерной графики как обработка изображений, 3D-моделирование, компьютерное зрение. Без тригонометрии были бы невозможны современные спецэффекты в кино и играх.
Перспективы развития тригонометрии
Несмотря на многовековую историю, тригонометрия продолжает активно развиваться и в наши дни. Создаются новые разделы этой науки, такие как p-адическая тригонометрия, изучающая тригонометрические функции в p-адических числовых полях. Разрабатывается тригонометрия на графах, гиперболических поверхностях и других математических объектах.
В области прикладных задач тригонометрия находит все новые области применения. Например, в последнее время активно развиваются тригонометрические методы анализа финансовых рынков, позволяющие прогнозировать изменение стоимости активов.
Тригонометрия в повседневной жизни
Что означает слово "тригонометрия" для обычного человека, далекого от математики и науки? На первый взгляд, совсем ничего. Однако на самом деле результаты, полученные с помощью тригонометрии, мы используем каждый день.
Например, системы GPS-навигации, которыми сегодня оснащены практически все гаджеты и автомобили. Их работа целиком основана на данных о расположении спутников, получаемых методами тригонометрии.
Другой яркий пример - современные мобильные сети связи. Для их проектирования необходимо тригонометрическими методами рассчитывать зоны покрытия базовых станций и оптимально размещать их на местности.
Популяризация тригонометрии
Несмотря на фундаментальную важность тригонометрии, уровень знаний в этой области среди широких масс остается невысоким. Многие воспринимают эту науку как нечто очень сложное и оторванное от реальной жизни.
Поэтому остро стоит задача популяризации тригонометрии, просвещения людей о ее достижениях и роли в развитии общества. Это позволит привлечь молодежь к изучению точных наук и подготовить новое поколение инженеров и ученых, способных развивать тригонометрию дальше.