Интеграл является одним из фундаментальных понятий математического анализа наряду с производной. Интегрирование, или нахождение интегралов, широко используется для решения задач в различных областях - от физики и инженерии до экономики и биологии. Освоение методов интегрирования крайне важно для понимания прикладной математики.
Несмотря на кажущуюся абстрактность, интеграл подчиняется вполне конкретным правилам. Зная основные приемы интегрирования, решение многих интегралов сводится к рутинной процедуре. В этой статье мы разберем полезные советы и тонкости, которые помогут научиться быстро и правильно находить интегралы.
Применение таблицы основных интегралов
Один из самых простых способов найти интеграл - это воспользоваться таблицей основных интегралов. В ней содержатся наиболее распространенные интегральные выражения вместе с их решениями. Часто для нахождения интеграла достаточно просто найти нужную запись в таблице.
Например, если необходимо найти интеграл от x2, то в таблице есть готовая запись: ∫x2dx = x3/3 + C. Таким образом, ответом будет x3/3 + C, где C - произвольная константа.
| ∫sin(x)dx | -cos(x) + C |
| ∫e^x dx | e^x + C |
Как видно из примеров, использование таблицы основных интегралов значительно упрощает нахождение многих интегралов, особенно степенных, тригонометрических, показательных и логарифмических функций.

Метод замены переменной при интегрировании
Еще один полезный прием при нахождении интегралов - это использование метода замены переменной. Суть его заключается в том, чтобы путем замены переменной интегрирования привести исходный интеграл к более простому виду.
Например, рассмотрим интеграл ∫sin2(3x)dx. Его можно решить непосредственно, но проще сделать замену u = 3x. Тогда du = 3 dx и интеграл примет вид:
∫sin2u × (1/3)du = (1/3)∫sin2u du
А ∫sin2u du - это стандартный интеграл, решение которого можно найти в таблице. Подставляя обратно вместо u переменную 3x, получаем ответ:
(1/3)(u - sin(u)cos(u))/2 + C =
(3x - sin(3x)cos(3x))/6 + C
Таким образом, благодаря замене переменной нам удалось свести исходный интеграл к табличному виду и значительно упростить его решение.
Интегрирование по частям сложных функций
Еще один мощный прием, позволяющий находить интегралы от сложных функций - это интегрирование по частям. Оно базируется на следующей формуле:
∫ u(x)v'(x)dx = u(x)v(x) - ∫ u'(x)v(x)dx
Где u(x) и v(x) - произвольные дифференцируемые функции. Суть метода состоит в разложении подынтегральной функции на произведение двух функций и последующем применении приведенной формулы.
Рассмотрим в качестве примера интеграл ∫x·e^x dx. Положим:
- u(x) = x
- v'(x) = e^x
Тогда:
- u'(x) = 1
- v(x) = e^x
И применяя формулу интегрирования по частям, получаем:
∫x·e^x dx = x·e^x - ∫1·e^x dx =
= x·e^x - e^x + C
Советы по нахождению определенных интегралов
При нахождении определенных интегралов часто возникают некоторые сложности. Рассмотрим несколько полезных советов, которые помогут справиться с ними.
Во-первых, необходимо как можно точнее вычислить неопределенный интеграл от данной функции и лишь затем подставлять пределы интегрирования. Иначе ошибки могут накапливаться на каждом этапе.
Во-вторых, перед вычислением определенного интеграла следует изучить поведение функции на заданном отрезке, найти точки разрыва, экстремумы и другие особенности. Это позволит правильно применить свойства интеграла и избежать ошибок:
- Если функция непрерывна на отрезке [a, b], то ∫ab f(x)dx = F(b) - F(a), где F(x) - первообразная f(x).
- Если в точке c функция разрывна, то необходимо разбивать интеграл на 2 части.
В-третьих, для некоторых функций есть специальные приемы вычисления определенного интеграла. Например, для степенных функций используют формулу:
∫axbxdx = (xb+1 - xa+1)/(b+1), при b ≠ -1
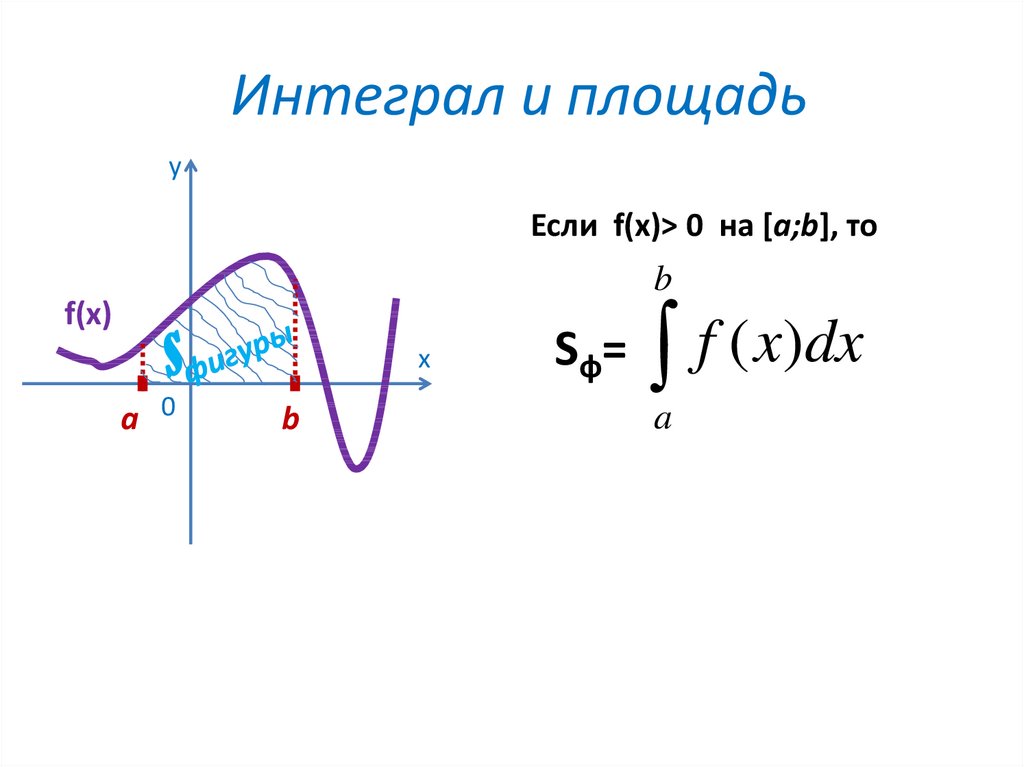
А для интегралов от тригонометрических функций есть несколько хитрых подстановок, упрощающих вычисления. С их помощью можно легко найти площадь под графиком sin(x) или cos(x).
Примеры решения типовых интегральных выражений
Для лучшего закрепления всех описанных выше приемов и методов нахождения интегралов рассмотрим несколько примеров решения наиболее типовых интегральных выражений.
1) ∫(3x2 + 5x + 1)dx. Это интеграл от многочлена. Применяя свойство линейности и пользуясь таблицей основных интегралов, имеем:
∫(3x2)dx + ∫(5x)dx + ∫(1)dx =
x3 + 5x2/2 + x + C
2) ∫tg(x)dx. Делаем замену u = tgx, du = (1/cos2x)dx. Тогда с учетом таблицы основных интегралов получаем:
∫tgxdx = ∫du = ln|cosx| + C
3) ∫xe2x dx. Применяем интегрирование по частям. Положим u = x, dv = e2x dx. Тогда:
∫xe2x dx = [x·(1/2)e2x] - ∫(1/2)e2x dx =
= (1/2)x·e2x - (1/4)e2x + C
























