В начале 19 века геометр из Берлина Якоб Штейнер поставил задачу, как соединить три деревни так, чтобы их протяженность была самой короткой. Впоследствии он обобщил эту задачу: требуется найти на плоскости такую точку, чтобы расстояние от нее до n других точек было наименьшим. В 20 веке продолжилась работа над этой темой. Было решено взять несколько точек и соединить их таким образом, чтобы расстояние между ними было самым коротким. Это все является частным случаем изучаемой проблемы.
"Жадные" алгоритмы
Алгоритм Краскала относится к "жадным" алгоритмам (их еще называют градиентными). Суть таковых – самый большой выигрыш на каждом шаге. Не всегда "жадные" алгоритмы дают наилучшее решение поставленной задачи. Существует теория, показывающая, что при их применении к определенным задачам они дают оптимальное решение. Это теория матроидов. Алгоритм Краскала относится к таким задачам.
Нахождение каркаса минимального веса
Рассматриваемый алгоритм строит оптимальный каркас графа. Задача о нем состоит в следующем. Дан неориентированный граф без кратных ребер и петель, и на множестве его ребер задана весовая функция w, которая приписывает каждому ребру e число – вес ребра – w(e). Вес каждого подмножества из множества ребер определяется суммой весов его ребер. Требуется найти каркас самого малого веса.
Описание
Алгоритм Краскала работает так. Сначала все ребра исходного графа располагаются в порядке возрастания весов. Первоначально каркас не содержит ни одного ребра, но включает все вершины графа. После очередного шага алгоритма к уже построенной части каркаса, которая является остовным лесом, добавляется одно ребро. Оно выбирается не произвольно. Все ребра графа, не принадлежащие каркасу, можно назвать красными и зелеными. Вершины каждого красного ребра находятся в одной компоненте связности строящегося леса, а вершины зеленого – в разных. Поэтому если добавить туда красное ребро, появляется цикл, а если зеленое – в полученном после этого шага лесе компонент связности будет меньше на одну. Таким образом, к полученному построению нельзя добавить ни одно красное ребро, но любое зеленое ребро прибавить можно, чтобы получить лес. И добавляется зеленое ребро с минимальным весом. В итоге получается каркас наименьшего веса.
Реализация
Обозначим текущий лес F. Он разбивает множество вершин графа на области связности (их объединение образует F, и они попарно не пересекаются). У красных ребер обе вершины лежат в одной части. Part(x) – функция, которая для каждой вершины x возвращает имя части, к которой принадлежит x. Unite(x,y) – это процедура, строящая новое разбиение, состоящее из объединения частей x и y и всех остальных частей. Пусть n – число ребер графа. Все эти понятия включены в алгоритм Краскала. Реализация:
Упорядочить все ребра графа от 1-го до n-го по возрастанию весов. (ai, bi – вершины ребра с номером i).
for i = 1 to n do.
x := Part(ai).
y : = Part(bi).
If x не равно y then Unite (x, y), включить в F ребро с номером i.
Корректность
Пусть T – каркас исходного графа, построенный с помощью алгоритма Краскала, а S – его произвольный каркас. Нужно доказать, что w(T) не превосходит w(S).
Пусть M – множество ребер S, P – множество ребер T. Если S не равно T, то найдется ребро et каркаса T, не принадлежащее S. Присоединим et к S. Образуется цикл, назовем его C. Удалим из C любое ребро es, принадлежащее S. Получится новый каркас, потому что и ребер, и вершин в нем столько же. Его вес не превосходит w(S), так как w(et) не больше w(es) в силу алгоритма Краскала. Эту операцию (замену ребер S на ребра T) будем повторять до тех пор, пока не получим Т. Вес каждого последующего полученного каркаса не больше веса предыдущего, откуда следует, что w(T) не больше, чем w(S).
Также корректность алгоритма Краскала следует из теоремы Радо-Эдмондса о матроидах.
Примеры применения алгоритма Краскала
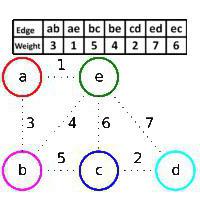
Дан граф с вершинами a, b, c, d, e и ребрами (a, b), (a, e), (b, c), (b, e), (c, d), (c, e), (d, e). Веса ребер показаны в таблице и на рисунке. Вначале строящийся лес F содержит все вершины графа и не содержит ни одного ребра. Алгоритм Краскала сначала добавит ребро (a, e), так как вес у него наименьший, и вершины a и e находятся в разных компонентах связности леса F (ребро (a, e) является зеленым), затем ребро (c, d), потому что у этого ребра наименьший вес из ребер графа, не принадлежащим F, и оно является зеленым, затем по тем же причинам добавляется ребро (a, b). А вот ребро (b, e) пропускается, хоть у него и наименьший вес из оставшихся ребер, потому что оно красное: вершины b и e принадлежат одной компоненте связности леса F, то есть если добавить к F ребро (b, e), образуется цикл. Затем добавляется зеленое ребро (b, c), пропускается красное ребро (c, e), а потом d, e. Таким образом, последовательно добавляются ребра (a, e), (c, d), (a, b), (b, c). Из нихер и состоит оптимальный каркас исходного графа. Так работает в данном случае алгоритм Краскала. Пример это показал.
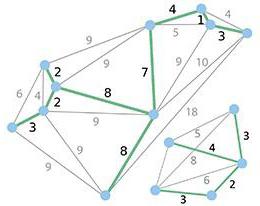
На рисунке показан граф, состоящий из двух компонент связности. Жирными линиями показаны ребра оптимального каркаса (зеленые), построенного с помощью алгоритма Краскала.
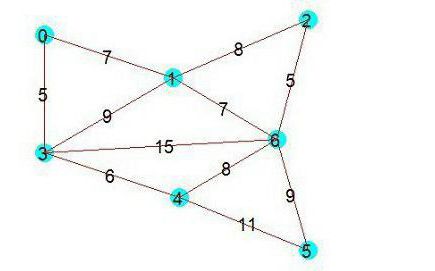
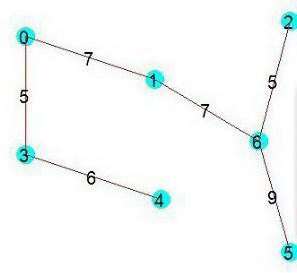
На верхнем рисунке изображен исходный граф, а на нижнем - каркас минимального веса, построенный для него с помощью рассматриваемого алгоритма.
Последовательность добавленных ребер: (1,6); (0,3), (2,6) или (2,6), (0,3) – значения не имеет; (3,4); (0,1), (1,6) или (1,6), (0,1), также безразлично (5,6).
Алгоритм Краскала находит практическое применение, например, для оптимизации прокладок коммуникаций, дорог в новых микрорайонах населенных пунктах каждой страны, а также в других случаях.


























