Прочитав данную статью, вы узнаете, как найти высоту конуса. Приведенный в ней материал поможет глубже разобраться в вопросе, а формулы окажутся весьма полезными в решении задач. В тексте разобраны все необходимые базовые понятия и свойства, которые обязательно пригодятся на практике.
Фундаментальная теория
Перед тем, как найти высоту конуса, необходимо разобраться с теорией.
Конус - фигура, которая плавно сужается от плоского основания (часто, хотя и необязательно, кругового) до точки, называемой вершиной.
Конус формируется набором отрезков, лучей или прямых, соединяющих общую точку с основанием. Последнее может ограничиваться не только окружностью, но и эллипсом, параболой или гиперболой.
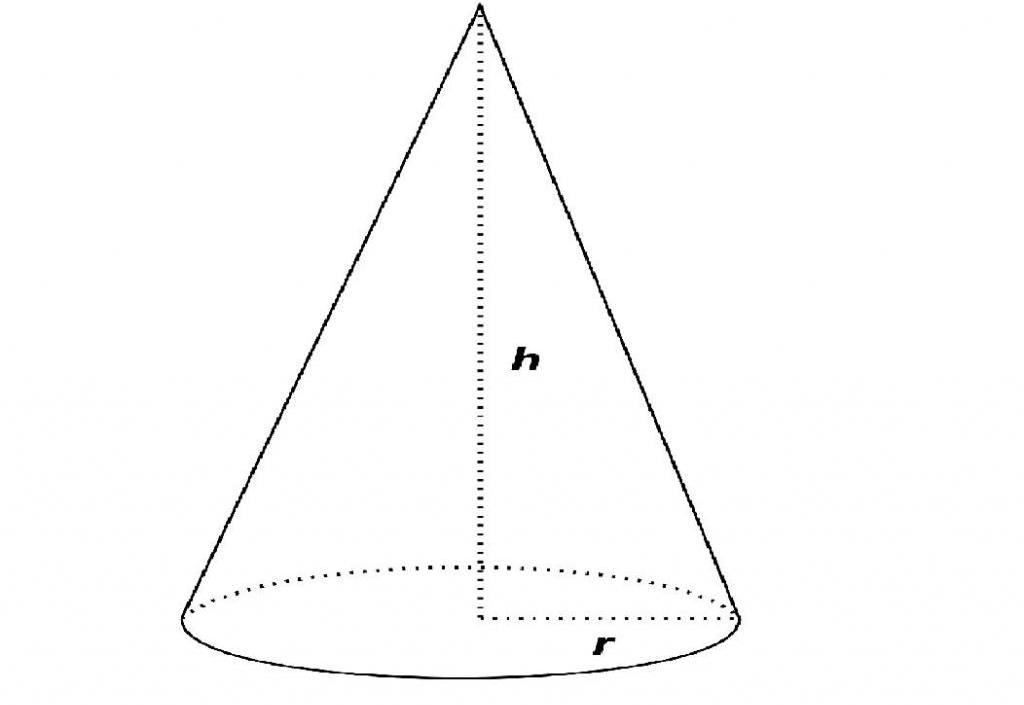
Ось - это прямая (если таковая имеется), вокруг которой фигура имеет круговую симметрию. Если угол между осью и основой составляет девяносто градусов, то конус принято называть прямым. Именно такая вариация чаще всего встречается в задачах.
Если в основе лежит многоугольник, то объект является пирамидой.
Отрезок, соединяющий вершину и линию, ограничивающую основание, называют образующей.
Как найти высоту конуса
Подойдем к вопросу с другой стороны. Для начала используем объем конуса. Чтобы его найти нужно вычислить произведение высоты с третьей частью площади.
V = 1/3 × S × h.
Очевидно, что из этого можно получить формулу высоты конуса. Достаточно лишь сделать правильные алгебраические преобразования. Разделим обе части равенства на S и умножим на тройку. Получим:
h = 3 × V × 1/S.
Теперь вы знаете, как найти высоту конуса. Однако для решения задач вам могут понадобиться и другие знания.
Важные формулы и свойства
Приведенный ниже материал однозначно поможет вам в решении конкретных задач.
Центр массы тела находится на четвертой части оси, начиная от основы.
В проективной геометрии цилиндр - это просто конус, вершина которого находится на бесконечности.
Следующие свойства работают только для прямого кругового конуса.
- Даны радиус основания r и высота h, тогда формула для площади будет выглядеть так: П × r2. Соответственно изменится и окончательное уравнение. V = 1/3 × П × r2 × h.
- Вычислить площадь боковой поверхности можно перемножив число "пи", радиус и длину образующей. S = П × r × l.
- Пересечение произвольной плоскости с фигурой является одним из конических сечений.
Часто встречаются задачи, где необходимо использовать формулу для объема усеченного конуса. Она выводится из обычной и имеет такой вид:
V = 1/3 × П × h × (R2 + Rr + r2), где: r -радиус нижнего основания, R - верхнего.
Всего этого будет вполне достаточно для решения разнообразнейших примеров. Разве что могут понадобиться знания, не связанные с этой темой, например, свойства углов, теорема Пифагора и другое.




















