Если сказать просто и кратко, то область определения - это те значения, которые может принимать какая-либо функция. Для того чтобы до конца исследовать эту тему, нужно поэтапно разобрать следующие пункты и понятия. Для начала давайте разберемся с определением функции и историей его появления.
Что такое функция
Все точные науки предоставляют нам множество примеров, когда рассматриваемые переменные каким-то образом зависят одна от другой. Например, плотность вещества полностью определяется его массой и объемом. Давление идеального газа при постоянном объеме варьируется вместе с температурой. Эти примеры объединяет тот факт, что все формулы имеют зависимости между переменными, которые и называются функциональными.

Функция - это понятие, выражающее зависимость одной величины от другой. Имеет вид y = f(x), где у - значение функции, которое зависит от х - аргумента. Таким образом, можно сказать, что у - переменная, зависимая от значения х. Значения, которые может принимать х, в совокупности составляют область определения заданной функции (D(y) или D(f)), а соответственно, значения у составляют множество значений функции (E(f) или E(y)). Бывают случаи, когда функция задана какой-либо формулой. В таком случае область определения состоит из значения таких переменных, при котором запись с формулой имеет смысл.
Есть совпадающие или равные функции. Это две функции, у которых равны области допустимых значений, а также значения самой функции равны при всех одинаковых аргументах.
Многие законы точных наук называются аналогично ситуациям в реальной жизни. Есть такой интересный факт также и о математической функции. Существует теорема о пределе функции, "зажатой" между двумя другими, имеющими одинаковый предел, - о двух полицейских. Объясняют ее так: раз уж два полицейских ведут между собой заключенного в камеру, то преступник вынужден туда идти, и выбора у него просто нет.
Историческая справка о функции
Понятие функции не сразу стало окончательным и точным, оно претерпело длинный путь становления. Сначала в работе Ферма «Введение и изучение плоских и телесных мест», которую опубликовали в конце 17-го века, говорилось следующее:
Всякий раз, когда в заключительном уравнении имеются две неизвестные величины, налицо имеется место.
В целом этот труд говорит о функциональной зависимости и ее материальном изображении (место = линия).
Также приблизительно в это же время Рене Декарт изучал линии по их уравнениям в своей работе "Геометрия" (1637 год), где опять же прослеживался факт зависимости двух величин друг от друга.
Само упоминание о термине "функция" появилось только в конце 17-го века у Лейбница, но не в современной его интерпретации. В своем научном труде он посчитал, что функция - это различные отрезки, связанные с какой-либо кривой линией.
Но вот уже в 18-м веке функцию начали определять более верно. Бернулли писал следующее:
Функция — это величина, составленная из переменной и постоянной.

Размышления Эйлера были также близки к этому:
Функция переменного количества есть аналитическое выражение, составленное каким-либо образом из этого переменного количества и чисел или постоянных количеств.
***
Когда некоторые количества зависят от других таким образом, что при изменении последних и сами они подвергаются изменению, то первые называют функциями вторых.

График функции
График функции составляют все точки, принадлежащие осям координатной плоскости, абсциссы которых принимают значения аргумента, а значения функции в этих точках являются ординатами.
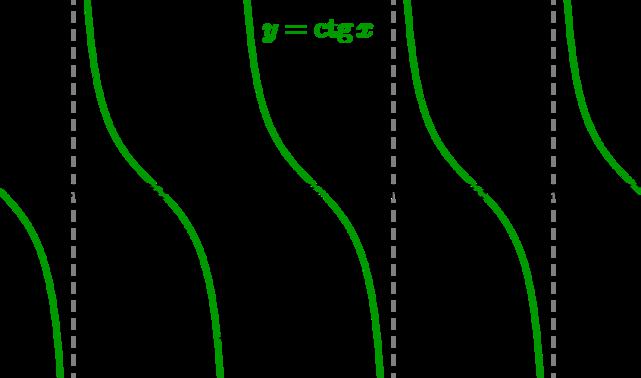
Область определения функции напрямую связана с ее графиком, потому что если какие-либо абсциссы исключаются областью допустимых значений, то нужно рисовать пустые точки на графике или же рисовать график в определенных пределах. Например, если берется график вида y = tgx, то из области определения исключается значение x = pi/2 +pi*n, n∉R, в случае с графиком тангенса нужно нарисовать вертикальные линии параллельно оси Оу (они называются асимптоты), проходящие через точки ±pi/2.
Любые основательные и тщательные исследования функций составляют большой раздел математики, который называется математическим анализом. В простейшей математике тоже затрагивают элементарные вопросы, касающиеся функций, например построение простого графика и установление некоторых основных свойств функции.
Чем может быть задана функция
Функция может:
- являться формулой, например: y = cos x;
- задаваться какой-либо таблицей из пар вида (х; у);
- сразу иметь графический вид, для этого пары из прошлого пункта вида (х; у) должны быть изображены на осях координат.
Будьте внимательны при решении некоторых заданий высокого уровня, практически любое выражение можно рассматривать как функцию относительно какого-либо аргумента для значения функции y (x). Найти область определения в таких заданиях может стать ключом к решению.
Для чего нужна область определения?
Первое, что нужно знать о функции для ее изучения или построения, - это ее область определения. График должен содержать только те точки, в которых функция может существовать. Область определения (х) может также называться областью допустимых значений (сокращенно ОДЗ).

Чтобы правильно и быстро построить график функций, вам необходимо знать область определения данной функции, потому что от нее зависит внешний вид графика и верность построения. Например, для построения функции y = √x нужно знать, что х может принимать только положительные значения. Поэтому строится только в первой координатной четверти.
Область определения на примере элементарных функций
В своем арсенале математика имеет малое количество простых, определенных функций. У них ограниченная область определения. Решение этого вопроса не вызовет сложностей даже в том случае, если перед вами оказалась так называемая сложная функция. Это всего лишь комбинация из нескольких простых.
- Итак, функция может являться дробной, например: f(x) = 1/x. Таким образом, переменная (наш аргумент) находится в знаменателе, а всем известно, что знаменатель дроби не может быть равным 0, следовательно, аргумент может принимать любые значения, кроме 0. Запись будет иметь следующий вид: D(y) = x∈ (-∞; 0) ∪ (0; +∞). Если в знаменателе будет какое-то выражение с переменной, то нужно решить уравнение относительно x и исключить значения, которые обращают знаменатель в 0. Для схематического изображения достаточно 5 грамотно выбранных точек. Графиком данной функции будет являться гипербола с вертикальной асимптотой, проходящей через точку (0; 0) и по совместительству оси Ох и Оу. Если графическое изображение будет пересекаться с асимптотами, то такая ошибка будет считаться грубейшей.
- Но какова же область определения у корня? Область определения у функции с подкоренным выражением (f(x) = √(2x + 5)), содержащим переменную, также имеет свои нюансы (имеет отношение только к корню четной степени). Так как арифметический корень является положительным или равным 0 выражением, то подкоренное выражение должно быть большим либо равным 0, решаем такое неравенство: 2х + 5 ≥ 0, х ≥ -2,5, следовательно, область определения данной функции: D(y) = x ∈ (-2,5; +∞). График представляет собой одну из ветвей параболы, повернутую на 90 градусов, находящуюся в первой координатной четверти.
- Если имеем дело с логарифмической функцией, то следует помнить, что действует ограничение касаемо основания логарифма и выражения под знаком логарифма, найти область определения в этом случае можно следующим образом. Имеем функцию: y = loga(х + 7), решаем неравенство: х + 7 > 0, х > -7. Тогда область определения этой функции - D(y) = x ∈ (-7; +∞).
- Также обращайте внимания на тригонометрические функции вида y = tgx и y = ctgx, так как y = tgx = sinx/cos/x и y = ctgx = cosx/sinx, следовательно, нужно исключить значения, при которых знаменатель может быть равен нулю. Если вы знакомы с графиками тригонометрических функций, разобраться в их области определения - это простая задача.
Чем отличается работа со сложными функциями
Помните несколько основных правил. Если работаем со сложной функцией, то не нужно что-то решать, упрощать, складывать дроби, приводить к наименьшему общему знаменателю и извлекать корни. Мы должны исследовать данную функцию, потому что различные (даже тождественные) операции могут изменить область определения функции, что приведет к получению неверного ответа.
Например, имеем сложную функцию: y = (x2 - 4)/(x - 2). Мы не можем сократить числитель и знаменатель дроби, так как это возможно, только если х ≠ 2, а это и является задачей поиска области определения функции, поэтому не раскладываем на множители числитель и не решаем никаких неравенств, ведь значение, при котором функция не существует, видно невооруженным взглядом. В данном случае х не может принимать значения 2, так как знаменатель не может обращаться в 0, запись будет выглядеть так: D(y) = x ∉ (-∞; 2) ∪ (2; +∞).
Взаимно-обратные функции
Для начала стоит сказать, что функция может стать обратимой только на промежутке возрастания или убывания. Для того чтобы найти обратную функцию, нужно в записи поменять местами х и у и решить уравнение относительно х. Области определения и области значения просто меняются местами.
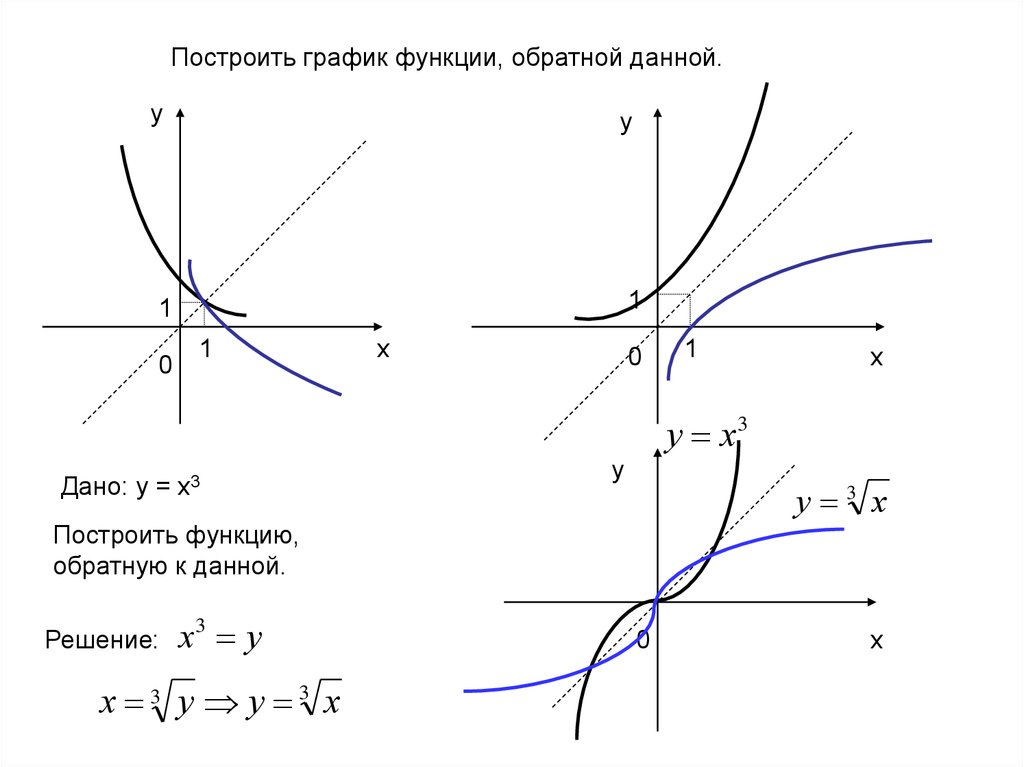
Главное условие обратимости - монотонный промежуток функции, если функция имеет промежутки возрастания и убывания, то можно составить обратную ей функцию какого-либо одного промежутка (возрастающего или убывающего).
Например, для экспоненциальной функции y = ex взаимно-обратной будет натуральная логарифмическая y = logea = lna. Для тригонометрических это будут функции с приставкой arc-: y = sinx и y = arcsinx и так далее. Графики будут располагаться симметрично по отношению к некоторым осям или асимптотам.
Выводы
Поиск области допустимых значений сводится к исследованию графика функций (если он есть), записи и решению необходимой конкретной системы неравенств.
Так, эта статья вам помогла понять, для чего нужна область определения функции и как ее найти. Надеемся, что она поможет вам хорошо разбираться в базовом школьном курсе.



























