Момент инерции маятника: определение, особенности и формула

При решении уравнений вращательного или колебательного (осциллирующего) движения необходимо знать момент инерции рассматриваемой системы. Данная статья посвящена изучению различного рода маятников и моменту инерции, которым они характеризуются.

Понятие о маятнике. Виды

Перед тем как приводить определение момента инерции маятника, необходимо рассмотреть, что собой представляет этот прибор. В физике под ним понимают абсолютно любую систему, которая может совершать колебания или вращение вокруг некоторой точки или оси под действием гравитационного поля, то есть силы тяжести. Это определение предполагает, что маятник в обязательном порядке должен обладать конечной массой, при этом центр масс системы не должен находиться в точке, через которую проходит ось вращения.

Существуют различные виды маятников. В данной статье рассмотрим только 3 из них:

• математический, или простой;
• физический (на примере однородного стержня);
• маятник Обербека.

Первые два являются маятниками колебательного типа, третий - вращательного.

Вращение и момент инерции

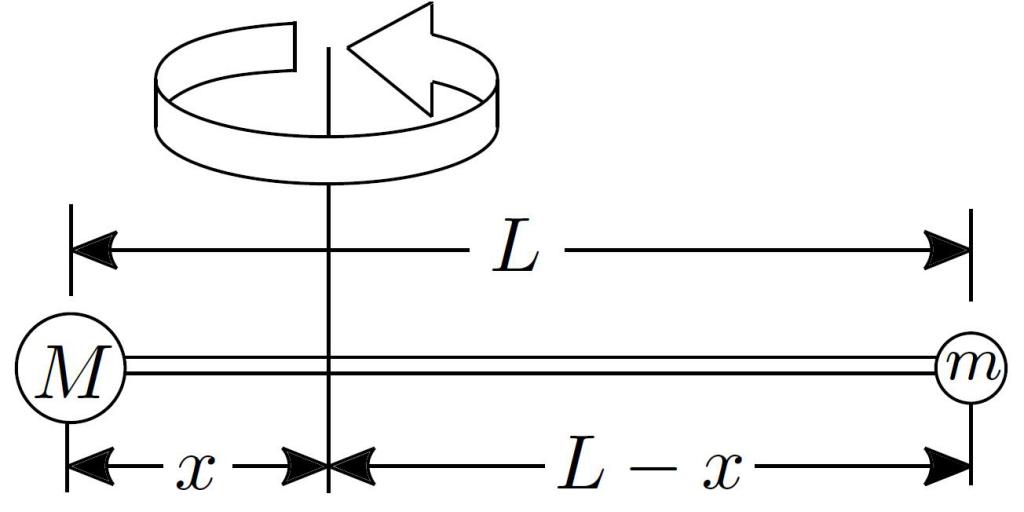
Когда тело с некоторой массой начинает вращаться вокруг оси, то его движение принято описывать следующим уравнением:

M = I*α.

Здесь M - это суммарный, или результирующий, момент всех внешних сил, которые действуют на систему, I - ее момент инерции и α - угловое ускорение.

Момент силы M по определению - это величина, равная произведению действующей силы на плечо, которое равно расстоянию от точки приложенной силы до оси вращения.

Момент инерции - величина, характеризующая инерционные свойства системы, то есть насколько быстро ее можно раскрутить, прилагая некоторый момент M. Также I характеризует запасенную вращающейся системой кинетическую энергию. Момент инерции I для материальной точки (воображаемый объект, масса которого сосредоточена в бесконечно малом объеме пространства), совершающей круговое движение на расстоянии от оси r, можно вычислить по следующей формуле:

I = m*r².

В общем же случае при определении I для тела произвольной формы следует пользоваться такими выражениями:

1) I = ∑m_i*r_i².

2) I = ∫dm *r_i² = ρ*∫dV *r_i².

Первое равенство применяется при дискретном расположении масс в системе, второе - при непрерывном.

Из этих выражений видно, что I является функцией расстояния до оси вращения и распределения массы в системе относительно этой оси и не зависит ни от прикладываемых моментов сил M, ни от скорости вращения ω.

Математический (простой) маятник

Поскольку этот вид колебательной системы является самым простым, то рассмотрим его подробнее. Маятник математический представляет собой материальную точку, которая подвешена на невесомой и нерастяжимой нити. Если эту точку отклонить слегка от положения равновесия, а затем отпустить, то она начнет совершать колебания. Также предполагается, что не существует сил трения в точке закрепления нити, и пренебрегают сопротивлением воздуха.

Как понятно из описания выше, математический маятник представляет собой идеальный случай, который не реализуется на практике. Тем не менее его изучение позволяет получить некоторые важные выводы для рассматриваемого типа движения.

Ниже на рисунке представлен этот маятник, а также обозначены действующие в системе силы при его колебании.

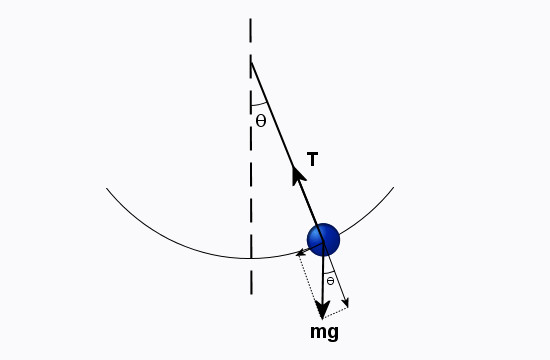
Применяя к нему уравнение движения, получаем следующее равенство:

M = -m*g*sin(θ)*L; I = m*L²; α = d²θ/dt² =>

=> -m*g*sin(θ)*L = m*L²*d²θ/dt², откуда:

L *d²θ/dt² + g*sin(θ) = 0.

Поясним некоторые моменты: момент силы от натяжения нити T (см. рис.) равен нулю, поскольку она действует непосредственно на ось; момент от силы тяжести взят со знаком минус, поскольку он направлен по часовой стрелке; L - длина нити; угловое ускорение α по определению является второй производной от угла поворота по времени либо первой производной по времени от угловой скорости ω; формула момента инерции маятника этого типа совпадает с таковой для материальной точки с массой m, находящейся от оси вращения на расстоянии L.

Полученное выше выражение можно упростить, если принять приближение: sin(θ)≈θ. Оно справедливо, когда углы колебания являются небольшими (до θ=10^o ошибка не превышает 0,5 %). В этом случае получаем:

L*d²θ/dt² + g*θ = 0.

Мы получили классическое дифференциальное уравнение (диф. ур.) второго порядка. Его решением является функция синуса:

θ = A*sin(ω*t+θ₀).

Здесь A и θ₀ - амплитуда колебаний и начальный угол отклонения от равновесия, соответственно. Если это решение подставить в диф. ур. выше, то можно получить угловую скорость и период колебаний:

ω = √(g/L) и T = 2*pi/ω = 2*pi*√(L/g).

Мы получили удивительный результат: период колебаний математического маятника не зависит от начальных условий (A и θ₀), а также от массы m.

Поведение математического маятника впервые начал изучать Галилей. Впоследствии Гюйгенс показал возможность использования полученной формулы для определения ускорения свободного падения Земли.

Физический маятник общего типа

Этот прибор представляет собой твердое тело произвольной формы (его масса может быть неравномерно распределена по его объему), которое совершает колебания относительно горизонтальной оси, не проходящей через центр масс тела.

При решении уравнения движения этого прибора рассматривают идеальный объект, масса которого сосредоточена в его центре тяжести. Такое предположение приводит к следующей формуле для периода его колебания:

T = 2*pi*√(I_o/(m*g*h)).

Здесь h - расстояние от центра тяжести до оси вращения O, I_o - момент инерции физического маятника. Заметим, что если для расчета момента силы тяжести можно воспользоваться свойством аддитивности этой величины и свести сумму всех моментов к одному, приложенному к центру тяжести, то для вычисления момента инерции I_o так поступать нельзя, его следует рассчитывать с использованием общих формул, которые были приведены ранее.

Колеблющийся стержень и его момент инерции

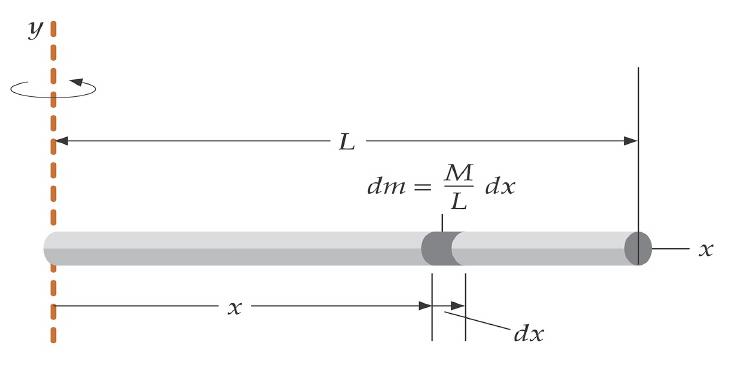
Представим себе, что имеется твердый стержень массой m и длиной L, который подвешен к одному из концов вертикально. Эта конструкция способна совершать колебания под действием земного притяжения.

Если применить интегрирование относительно оси к такому стержню, то можно получить, что момент инерции маятника физического указанной конструкции будет равен:

I_o = m*L²/3.

Тогда его период колебаний будет равен:

T = 2*pi*√(2*L /(3*g)).

Маятник Обербека

На рисунке ниже приведен этот вид маятника.

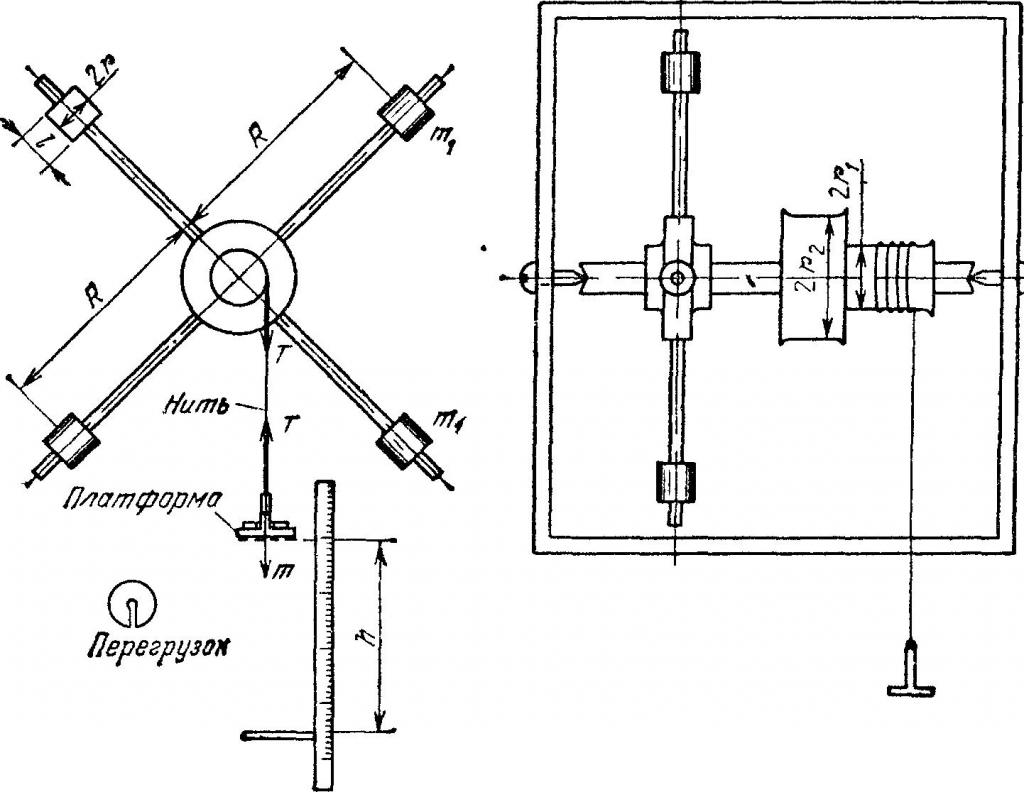
Из рисунка видно, если подвесить груз к нити, то 4 стержня с грузами начинают вращаться с некоторым угловым ускорением.

Маятник Обербека используется для проведения лабораторных работ по физике с целью проверки уравнения вращательного движения.

Определение момента инерции маятника Обербека

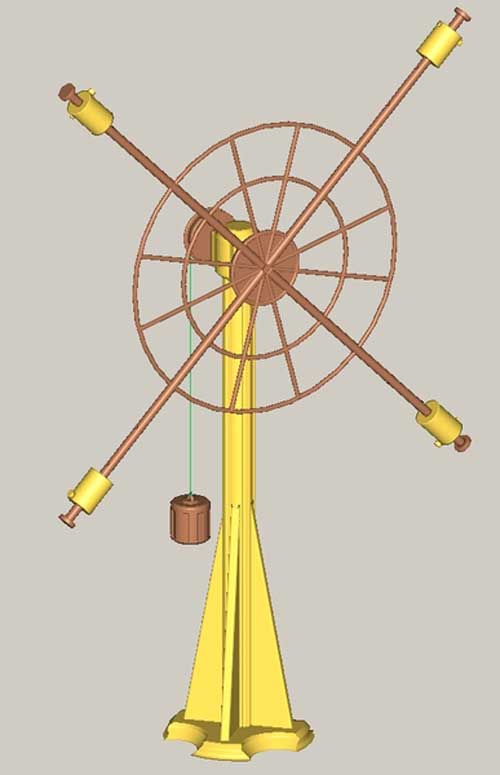
Для решения этой задачи необходимо сделать важное приближение: вес стержней и дисков, к которым подвешивается на нити перегрузок, является пренебрежимо малым по сравнению с весом одного груза m. Учитывая, что размер грузов намного меньше их расстояния до оси вращения, можно воспользоваться формулой для момента инерции материальной точки. Поскольку грузов 4 и все они имеют одинаковую массу, но расположены на разных расстояниях от оси, то получаем следующую формулу для момента инерции маятника Обербека:

I = I₁+I₂+I₃+I₄ = m*(R₁²+R₂²+R₃²+R₄² ).

Поскольку этот маятник позволяет регулировать положение каждого груза на стержне, то его момент инерции может изменяться.