Типичными линейными параметрами любой пирамиды являются длины сторон ее основания, высота, боковые ребра и апофемы. Тем не менее существует еще одна характеристика, которая связана с отмеченными параметрами, - это двугранный угол. Рассмотрим в статье, что он собой представляет и как его находить.
Пространственная фигура пирамида
Каждый школьник хорошо представляет, о чем идет речь, когда слышит слово "пирамида". Геометрически построить ее можно так: выбрать некоторый многоугольник, затем зафиксировать точку в пространстве и соединить ее с каждым углом многоугольника. Получившаяся объемная фигура будет пирамидой произвольного типа. Многоугольник, который ее образует, называется основанием, а точка, с которой соединены все его углы, является вершиной фигуры. Ниже на рисунке схематически показана пятиугольная пирамида.
Видно, что ее поверхность образована не только пятиугольником, но и пятью треугольниками. В общем случае число этих треугольников будет равно количеству сторон многоугольного основания.
Двугранные углы фигуры
Когда рассматриваются геометрические задачи на плоскости, то любой угол образован двумя пересекающимися прямыми, или отрезками. В пространстве же к этим линейным углам добавляются двугранные, образованные пересечением двух плоскостей.
Если отмеченное определение угла в пространстве применить к рассматриваемой фигуре, то можно сказать, что существует два вида двугранных углов:
- При основании пирамиды. Он образован плоскостью основания и любой из боковых граней (треугольником). Это означает, что углов при основании у пирамиды n, где n - число сторон многоугольника.
- Между боковыми сторонами (треугольниками). Количество этих двугранных углов также составляет n штук.
Заметим, что первый тип рассматриваемых углов строится на ребрах основания, второй тип - на боковых ребрах.
Как рассчитать углы пирамиды?
Линейный угол двугранного угла является мерой последнего. Вычислить его непросто, поскольку грани пирамиды, в отличие от граней призмы, пересекаются не под прямыми углами в общем случае. Надежнее всего проводить расчет значений двугранных углов с использованием уравнений плоскости в общем виде.
В трехмерном пространстве плоскость задается следующим выражением:
A*x + B*y + C*z + D = 0
Где A, B, C, D - это некоторые действительные числа. Удобством этого уравнения является то, что первые три отмеченных числа являются координатами вектора, который перпендикулярен заданной плоскости, то есть:
n¯ = [A; B; C]
Если известны координаты трех точек, принадлежащих плоскости, то, взяв векторное произведение двух векторов, построенных на этих точках, можно получить координаты n¯. Вектор n¯ называется направляющим для плоскости.
Согласно определению, двугранный угол, образованный пересечением двух плоскостей, равен линейному углу между их направляющими векторами. Предположим, что мы имеем две плоскости, нормальные векторы которых равны:
n1¯ = [A1; B1; C1];
n2¯ = [A2; B2; C2]
Для вычисления угла φ между ними можно воспользоваться свойством произведения скалярного, тогда соответствующая формула принимает вид:
φ = arccos(|(n1¯*n2¯)|/(|n1¯|*|n2¯|))
Или в координатной форме:
φ = arccos(|A1*A2 + B1*B2 + C1*C2|/(√(A12 + B12+C12)*√(A22 + B22 + C22)))
Покажем, как использовать изложенную методику расчета двугранных углов при решении геометрических задач.
Углы правильной пирамиды четырехугольной
Предположим, что имеется правильная пирамида, в основании которой находится квадрат со стороной 10 см. Высота фигуры равна 12 см. Необходимо вычислить, чему равны двугранные углы при основании пирамиды и для ее боковых сторон.
Поскольку заданная в условии задачи фигура является правильной, то есть обладает высокой симметрией, то все углы при основании равны друг другу. Также являются одинаковыми углы, образованные боковыми гранями. Чтобы вычислить необходимые двугранные углы, найдем направляющие векторы для основания и двух боковых плоскостей. Обозначим длину стороны основания буквой a, а высоту h.
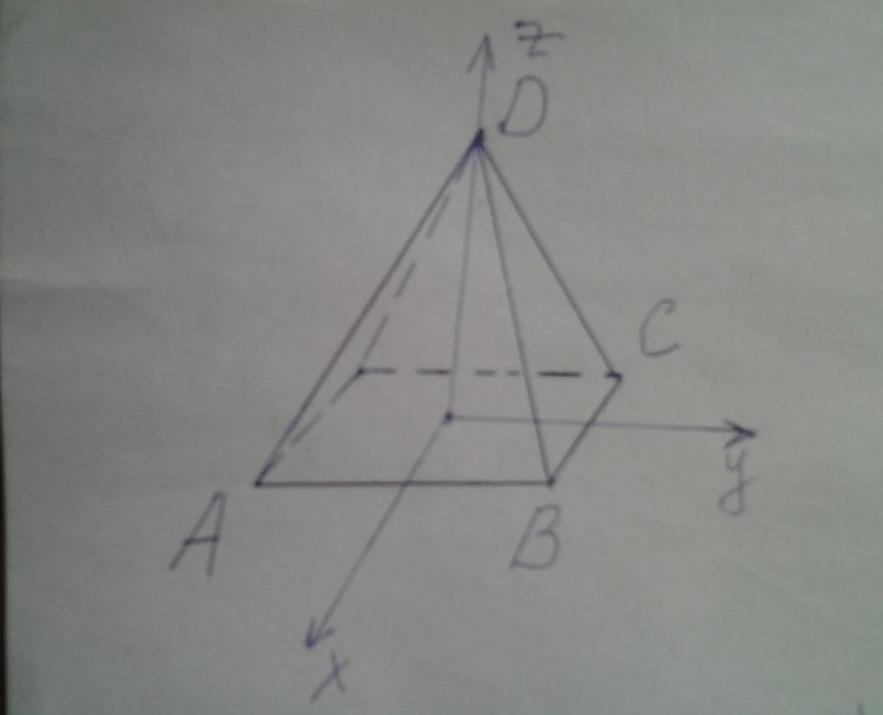
Рисунок выше показывает четырехугольную правильную пирамиду. Выпишем координаты точек A, B, C и D в соответствии с введенной системой координат:
A(a/2; -a/2; 0);
B(a/2; a/2; 0);
C(-a/2; a/2; 0);
D(0; 0; h)
Теперь найдем направляющие векторы для плоскостей основания ABC и двух боковых сторон ABD и BCD в соответствии с изложенной в пункте выше методикой:
Для ABC:
AB¯ = (0; a; 0); AC¯ = (-a; a; 0); n1¯ = [AB¯*AC¯] = (0; 0; a2)
Для ABD:
AB¯ = (0; a; 0); AD¯ = (-a/2; a/2; h); n2¯ = [AB¯*AD¯] = (a*h; 0; a2/2)
Для BCD:
BC¯ = (-a; 0; 0); BD¯ = (-a/2; -a/2; h); n3¯ = [BC¯*BD¯] = (0; a*h; a2/2)
Теперь остается применить соответствующую формулу для угла φ и подставить значения стороны и высоты из условия задачи:
Угол между ABC и ABD:
(n1¯*n2¯) = a4/2; |n1¯| = a2; |n2¯| = a*√(h2 + a2/4);
φ = arccos(a4/2/(a2*a*√(h2 + a2/4))) = arccos(a/(2*√(h2 + a2/4))) = 67,38o
Угол между ABD и BDC:
(n2¯*n3¯) = a4/4; |n2¯| = a*√(h2 + a2/4) ; |n3¯| = a*√(h2 + a2/4);
φ = arccos(a4/(4*a2*(h2+a2/4)) = arccos(a2/(4*(h2+a2/4))) = 81,49o
Мы вычислили значения углов, которые требовалось найти по условию задачи. Полученные при решении задачи формулы можно использовать для определения двугранных углов четырехугольных правильных пирамид с любыми значениями a и h.
Углы треугольной правильной пирамиды
На рисунке ниже дана пирамида, основанием которой является правильный треугольник. Известно, что двугранный угол между боковыми сторонами является прямым. Необходимо вычислить площадь основания, если известно, что высота фигуры равна 15 см.
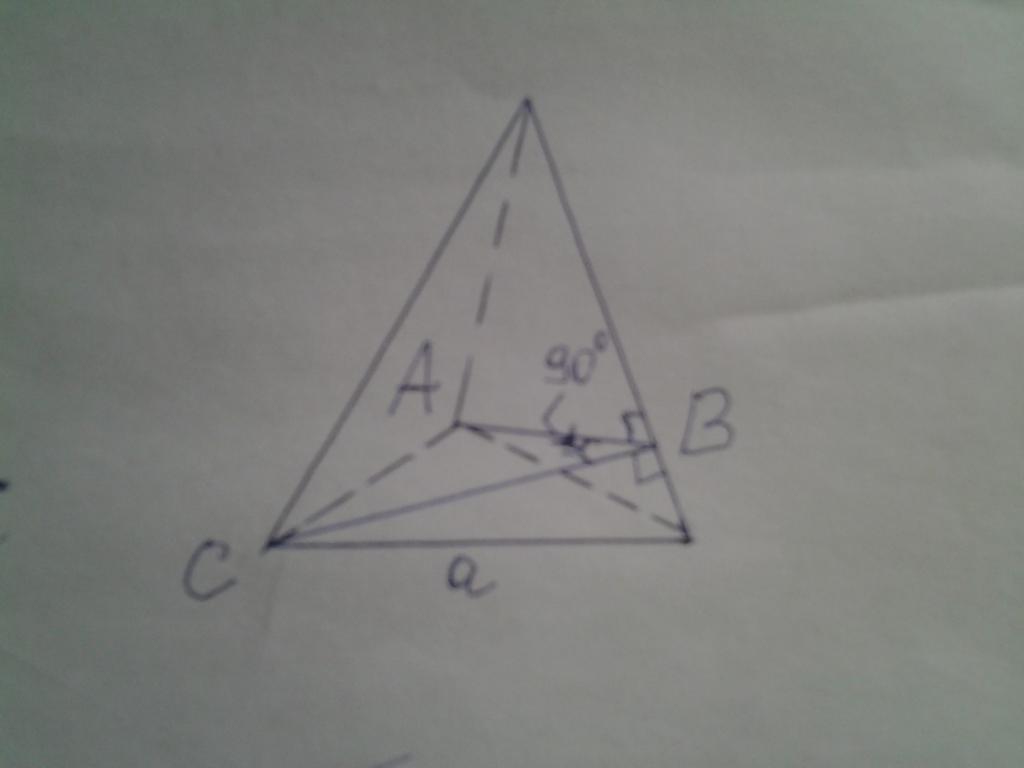
Двугранный угол, равный 90o, на рисунке обозначен как ABC. Решить задачу можно, применяя изложенную методику, однако в данном случае поступим проще. Обозначим сторону треугольника a, высоту фигуры - h, апофему - hb и боковое ребро - b. Теперь можно записать следующие формулы:
S = 1/2*a*hb;
b2 = hb2 + a2/4;
b2 = h2 + a2/3
Поскольку два боковых треугольника в пирамиде являются одинаковыми, то стороны AB и CB равны и являются катетами треугольника ABC. Обозначим их длину x, тогда:
x = a/√2;
S = 1/2*b*a/√2
Приравнивая площади боковых треугольников и подставляя апофему в соответствующее выражение, имеем:
1/2*a*hb = 1/2*b*a/√2 =>
hb = b/√2;
b2 = b 2/2 + a2/4 =>
b = a/√2;
a2/2 = h2 + a2/3 =>
a = h*√6
Площадь равностороннего треугольника рассчитывается так:
S = √3/4*a2 = 3*√3/2*h2
Подставляем значение высоты из условия задачи, получаем ответ: S = 584,567 см2.


























