Школьный курс геометрии делится на два больших раздела: планиметрию и стереометрию. Стереометрия изучает пространственные фигуры и их характеристики. В данной статье мы рассмотрим, что такое прямая призма, и приведем формулы, описывающие такие ее свойства, как длины диагоналей, объем и площадь поверхности.
Что такое призма?
Когда школьников просят назвать определение призмы, то они отвечают, что данная фигура представляет собой два одинаковых параллельных многоугольника, стороны которых соединены параллелограммами. Это определение является максимально общим, поскольку оно не накладывает условия на форму многоугольников, на их взаимное расположение в параллельных плоскостях. Кроме того, оно предполагает наличие соединяющих параллелограммов, к классу которых также относятся квадрат, ромб и прямоугольник. Ниже можно посмотреть, что собой представляет четырехугольная призма.

Мы видим что призма - это многогранник (полиэдр), состоящий из n + 2 сторон, 2 × n вершин и 3 × n ребер, где n - количество сторон (вершин) одного из многоугольников.
Оба многоугольника принято называть основаниями фигуры, остальные грани - это боковые стороны призмы.
Понятие о прямой призме
Существуют призмы различных видов. Так, говорят о правильных и неправильных фигурах, о треугольных, пятиугольных и других призмах, бывают выпуклые и вогнутые фигуры, наконец, они бывают наклонными и прямыми. О последних поговорим подробнее.
Прямая призма - это такая фигура изучаемого класса полиэдров, все боковые четырехугольники которой имеют прямые углы. Существует всего два типа таких четырехугольников - это прямоугольник и квадрат.
Рассматриваемый вид фигуры обладает важным свойством: высота призмы прямой равна длине ее бокового ребра. Отметим, что все боковые ребра фигуры равны между собой. Что касается боковых граней, то в общем случае они друг другу не равны. Их равенство возможно если, помимо того что призма является прямой, будет еще правильной.
Ниже рисунок демонстрирует прямую фигуру с пятиугольным основанием. Видно, что все ее грани боковые - это прямоугольники.
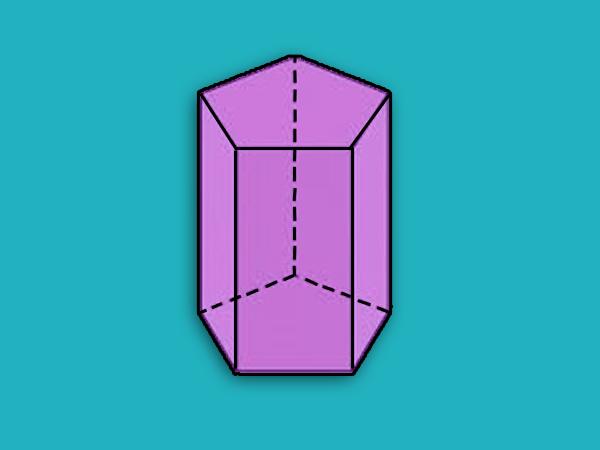
Диагонали призмы и ее линейные параметры
Основными линейными характеристиками любой призмы являются ее высота h и длины сторон ее основания ai, где i = 1, ..., n. Если основание является многоугольником правильным, тогда для описания его свойств достаточно знать длину a одной стороны. Знание отмеченных линейных параметров позволяет однозначно определить такие свойства фигуры, как ее объем или поверхность.
Диагонали прямой призмы представляют собой отрезки, которые соединяют любые две несмежные вершины. Такие диагонали могут быть трех типов:
- лежащие в плоскостях основания;
- находящиеся в плоскостях боковых прямоугольников;
- принадлежащие объему фигуры.
Длины тех диагоналей, что относятся к основанию, следует определять в зависимости от типа n-угольника.
Диагонали боковых прямоугольников рассчитываются по следующей формуле:
d1i = √(ai2 + h2).
Для определения объемных диагоналей необходимо знать значение длины соответствующей диагонали основания и высоты. Если некоторую диагональ основания обозначить буквой d0i, тогда объемная диагональ d2i вычисляется так:
d2i = √(d0i2 + h2).
Например, в случае правильной четырехугольной призмы длина объемной диагонали будет равна:
d2 = √(2 × a2 + h2).
Отметим, что прямая треугольная призма обладает лишь одним из трех названных типов диагоналей: диагональю боковой стороны.
Поверхность изучаемого класса фигур
Площадь поверхности представляет собой совокупность площадей всех граней фигуры. Чтобы наглядно себе представить все грани, следует сделать развертку призмы. В качестве примера такая развертка для пятиугольной фигуры приведена ниже.
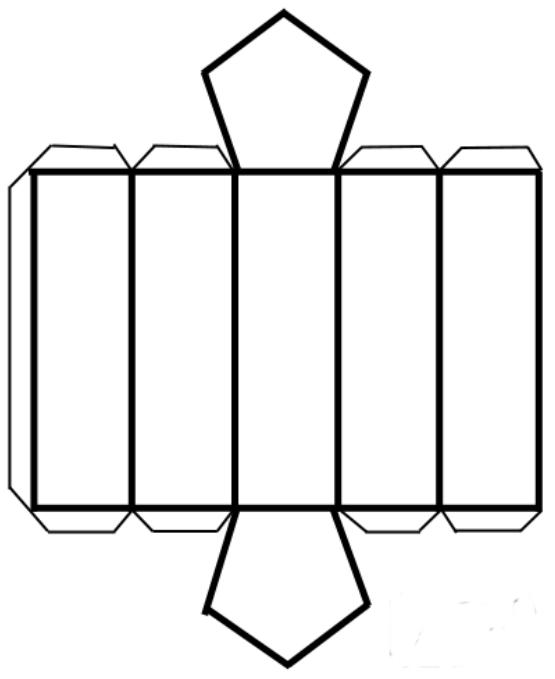
Мы видим, что количество плоских фигур равно n + 2, причем n - это прямоугольники. Чтобы рассчитать площадь всей развертки, следует сложить площади двух одинаковых оснований и площади всех прямоугольников. Тогда соответствующая формула будет иметь вид:
S = 2 × So + h × ∑i=1n (ai).
Из этого равенства видно, что площадь боковой поверхности для изучаемого вида призм равна произведению высоты фигуры на периметр ее основания.
Площадь основания So можно рассчитать, применяя соответствующую геометрическую формулу. Например, если основание прямой призмы - прямоугольный треугольник, тогда получаем:
So = a1 × a2 / 2.
Где a1 и a2 - катеты треугольника.
Если же основание представляет собой n-угольник с равными углами и сторонами, тогда будет справедливым применение такой формулы:
So = n / 4 × ctg (pi / n) × a2.
Формула объема

Определение объема призмы любого вида не является сложной задачей, если известны значения ее площади основания So и высоты h. Перемножив эти значения между собой, мы получим объем V фигуры, то есть:
V = So × h.
Поскольку у прямой призмы параметр h равен длине ребра бокового, то вся проблема вычисления объема сводится к расчету площади So. Выше мы уже сказали несколько слов и привели пару формул, позволяющих определить So. Здесь лишь отметим, что в случае основания произвольной формы, следует разбить его на простые сегменты (треугольники, прямоугольники), рассчитать площадь каждого, а затем сложить все площади, чтобы получить So.



























