Геометрия является одним из важных разделов математики. В нем изучаются пространственные свойства фигур. Одной из них является многогранник под названием призма. Данная статья посвящена ответам на вопросы, что такое призма и какие формулы применяются для расчета ее основных свойств.
Многогранник - призма
Начнем статью сразу с ответа на вопрос, что такое призма. Под ней понимают объемный многогранник, который состоит из двух многоугольных и параллельных друг другу оснований и нескольких параллелограммов или прямоугольников. Чтобы лучше представить, о каком классе фигур пойдет речь, ниже показан пример призмы пятиугольной.
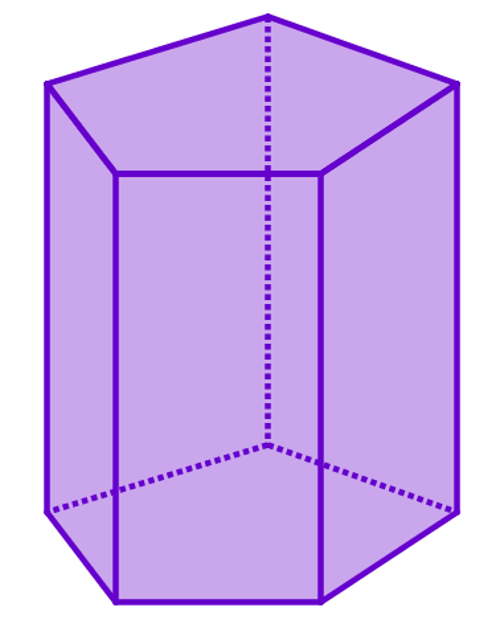
Как видно, два пятиугольника лежат в параллельных плоскостях и равны между собой. Их стороны соединены пятью прямоугольниками, в данном случае. Из этого примера следует, что если основанием фигуры является многоугольник с числом сторон n, то количество вершин призмы будет равно 2 * n, число ее граней составит n + 2, а число ребер будет равно 3 * n. Нетрудно показать, что количества этих элементов удовлетворяют теореме Эйлера:
3 * n = 2 * n + n + 2 - 2.
Выше, когда давался ответ на вопрос, что такое призма, мы упомянули, что грани, соединяющие одинаковые основания, могут быть параллелограммами или прямоугольниками. Заметим, что вторые относятся к классу первых. Кроме того, возможен случай, когда эти грани будут представлять собой квадраты. Стороны, которые соединяют основания призмы, называются боковыми. Их количество определяется числом углов или сторон многогранного основания.
Кратко упомянем, что значение слова "призма" происходит от греческого языка, где оно означало буквально "отпиленный". Несложно понять, откуда такое название произошло, если посмотреть на четырехугольные деревянные призмы на рисунке ниже.

Какие бывают призмы?
Классификация призм предполагает рассмотрение различных характеристик этих фигур. Так, в первую очередь учитывают многоугольность основания, поэтому говорят о треугольных, четырехугольных и других призмах. Во-вторых, форма боковых граней определяет, является ли фигура прямой, или же она будет наклонной. У прямой фигуры все боковые грани имеют по четыре прямых угла, то есть это либо прямоугольники, либо квадраты. У наклонной же фигуры эти грани представляют собой параллелограммы.
К особой категории относятся правильные призмы. Дело в том, что у них основания представляют собой равносторонние и равноугольные многоугольники, а сама фигура является прямой. Эти два факта говорят о том, что боковые стороны у таких фигур все равны между собой.

Наконец, еще одним критерием классификации является выпуклость или вогнутость основания. Например, вогнутая фигура в виде пятиконечной звезды показана выше на рисунке.
Формулы площади и объема правильной фигуры
Разобравшись, что такое правильная призма, приведем две главные формулы, с помощью которых можно определить их объем и площадь поверхности.
Поскольку площадь S всей фигуры образована из двух оснований с n сторонами и n прямоугольниками, то для ее вычисления следует пользоваться такими выражениями:
So = n / 4 * ctg(pi / n) * a2;
S = 2 * So + n * a * h.
Здесь So - одного основания площадь, a - сторона этого основания, h - высота всей фигуры.
Для вычисления объема рассматриваемого вида призм следует применять формулу:
V = So * h = n / 4 * ctg(pi / n) * a2 * h.
Вычисление величин S и V для правильных фигур требует знания всего двух линейных геометрических параметров.
Треугольная стеклянная призма
Что такое призма, мы разобрались. Это совершенный объект геометрии, применяют его для придания форм многим сооружениям и предметам. Отметим лишь одно из важных применений ее формы в физике. Речь идет о треугольной призме, изготовленной из стекла. Благодаря ее форме, падающий на нее свет, в результате дисперсии разлагается на несколько цветов, что позволяет анализировать химический состав излучателя.























