Дифференцирование и интегрирование представляют собой уравнение, содержащее производные. Последние, если придерживаться математическим свойствам, разделяются на обычные и частные. Производные представляют скорость изменения, а дифференциальное уравнение описывает взаимосвязь между величиной, которая постоянно видоизменяется в процессе решения, образуя новые переменные.
Профессор университета с легкостью сориентируется в сложных операциях с интегралами, преобразует их в одно целое, а потом докажет исчисления обратным методом. Однако возможность быстро вспоминать детали сложных формул доступна не каждому человеку, потому рекомендуется освежить память или открыть для себя новый материал.
Значение и основное применение
В научной литературе производная определяется, как скорость, подверженная преобразованию функции на основе одной из ее переменных. Дифференциация - это сущность исчисления, которую можно сравнить с началом поисков касательной к точке. Как известно, последняя имеет различные виды и требует вычислительных формул для поиска. Предположим, вам требуется найти наклон касательной к графику в точке Р. Как это сделать? Достаточно провести дугообразную полосу через обозначенный объект и поднять ее вверх, пока мы не получим секущуюся линию.

Функция f в х называется дифференцируемой в точке х = а, если производная f '(а) существует на каждом обозначении ее области. Продемонстрируем пример:
f '(а) = lim (h=0) × f(а + h) – f(а)/h
Для того чтобы уравнение подвергнуть дифференцированию и интегрированию функций так, что ее расположение станет возможным в любой точке x, она не должна прерываться. Заранее построив схематичное изображение вы сможете убедиться в достоверности утверждения. Именно по этой причине область f '(х) определяется существованием ее пределов.
Предположим, что у = f(х) – функция из х, то производная от f(х) задается как dy/dx. Также она определяется, как линейное уравнение, где необходимо найти необходимые данные по у.
Однако, если мы ищем производную от у в первом случае, то в следующем предстоит найти f(x) от x.
d/dx × (f(x)) la или df/dx la
Следовательно, обозначение скорости изменения функции f(x) относительно x в точке a, лежащей на ее поверхности.
Если известна производная f', которая дифференцируема в своей области, то мы можем найти ее значение f. В интегральном исчислении мы называем f антипроизводной или примитивом функции f '. Метод его расчета известен, как антидифференцирование или интеграция.
Виды и формы
Уравнение с одним или несколькими членами, которое включает производные зависимой переменной по независимой, известно, как дифференциал. Иначе говоря, он состоит из множества числовых значений, обычных или частных, подвергающихся изменениям в процессе решения.

На данный момент существуют следующие типы дифференциальных уравнений.
Обыкновенные. Простое равенство, напрямую зависящее от переменной:
dy/dx + 5x = 5y
С частными производными:
dy/dx + dy/dt = x3-t3
d2y/dx2 – c2 × d2y/dt2
Старшего коэффициента. Данному виду характерно участие в порядке дифференциального уравнения, как продемонстрировано на примере ниже, где он равен 3. Число считается наивысшим из присутствующих:
d3y/dx2 + 5 × dy/dx + y = √x
Функции могут иметь несколько видов, однако, предпочтительным является использование одинарной кавычки с характерными формулами интегрирования и дифференцирования.
y’ = dy/dx
y’’ = d2y/dx2
y’’’ = d3y/dx3
Линейное. Переменная, фигурирующая в уравнении, возводится в степень единицы. График такого вида функций обычно является прямой линией. Например, (3x + 5), но (x3 + 4x2) не относится к данному типу, поскольку требует другого решения.
dy/dx + xy = 5x
Нелинейное. Любое интегрирование и дифференцирование рядов с двойственными способами получения равенства – относятся к рассматриваемому виду:
d2y/dx2- ln y = 10
Методы быстрого получения результата
Недостаточно рассмотреть форму, чтобы разобраться как справиться и применить на практике полученные знания. В настоящее время существует несколько способов решения дифференциального уравнения.

Это:
- Разделение переменной. Выполняется, когда пример можно изобразить в качестве dy / dx = f(y) g(x). Особенность заключается в том, что f и g – функции, принадлежащие к своим значениям. Благодаря этому, задачу следует преобразить: 1/ f(y) dy = g(x) dx. И только после перейти к следующему пункту.
- Метод интегрирующего фактора. Используется, когда пример имеет вид dy / dx + р(x) y = q(x), где р и q являются функциями только x.
Дифференциальный вычисления первого порядка выглядят, как y'+ Р(х) y = Q (x), поскольку они содержат необходимые функции и производную от y. Последующее увеличение в наименовании действует по тому же принципу. Например, производные от неизвестной функции, могут оказаться как частными, так и обычными.
Неопределенные интегралы
Если вам предоставлена скорость вашего велосипеда, когда вы отправились на прогулку, в зависимости от времени - сможете ли вы рассчитать пройденное расстояние, используя данные о потраченных минутах? Данная задача выглядит непосильной ношей, однако интегралы помогут справиться с этими свойствами максимально эффективно, получив результат.
Научная литература акцентирует внимание на том, что они являются обратной стороной дифференцирования. Действительно, интеграция - это метод сложения вещей. Он соединяет частички между собой, создавая нечто новое – целое. Главное в любом схожем примере: найти неопределенные интегралы и проверить результаты интегрирования дифференцированием. Это поможет избежать лишних ошибок.
Если вы собираетесь искать площадь любой случайной кривой, например, y=f(x), то воспользуйтесь рассматриваемым методом. Помните, что только внимательность спасет вас от ошибки.
Формулы для решения
Так, познакомившись с основной концепцией дифференцирования и интегрирования - обратного вычисления через функции, необходимо кратко рассмотреть некоторые основы. Они приведены ниже.
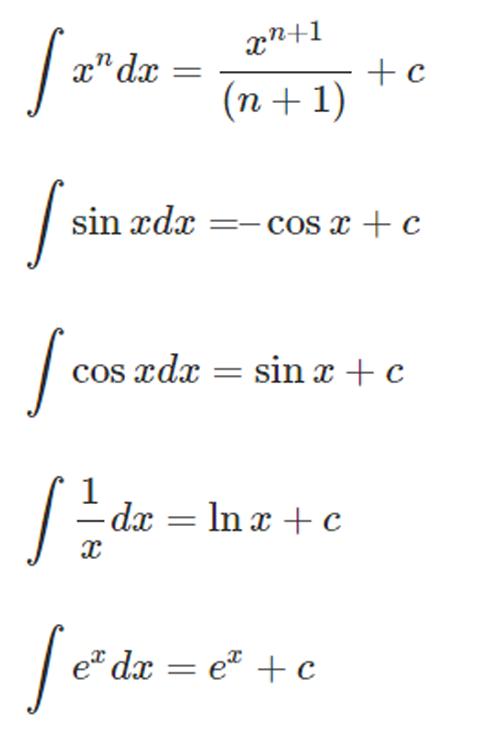
Основные правила вычисления
Такие интегрированные функции, как f (x) легко перевести в равенство, если представить уравнение, как: ∫ f(x) dx = F(x) + C.
Здесь F (x) называется антипроизводной или примитивной. f(x) - подынтегральная функция. dx – выступает, как дополнительный числовой агент. С - интегрированная или произвольная постоянная. x – выступает в зависимости от стороны равенства.
Из приведенного выше утверждения, можно сделать вывод, что интегрирование и дифференцирование рядов – два противоположных друг от друга процесса. Вместе они выступают, как одна из видов операций, направленная на получение итогового результата, выполняемого над самим уравнением.
Теперь, когда мы больше знаем об особенностях исчисления, рекомендуется выделить преимущественные отличия, необходимые для дальнейшего понимания:
- Дифференцирование и интегрирование способны одновременно удовлетворять правилам линейности.
- Операции направлены на поиск максимально точного решения, однако, предполагают ограничения для их определения.
- При дифференцировании полиномиального примера результат на 1 меньше, чем степень функции, тогда как в случае интегрирования полученный результат преобразуется в другой, действуя по противоположной схеме.
- Два вида решения, как говорилось ранее, являются противоположными друг другу. Они вычисляются по формулам интегрирования и дифференцирования.
- Производная любой функции уникальна, но, с другой стороны, два интеграла, в одном примере, могут отличаться на константу. Именно это правило представляет главную сложность во время выполнения задач.
- Имея дело с производными, мы можем рассматривать производные в точке. Почти как и в интегралах они предоставляют функции по интервалу.
- Геометрически производная описывает скорость изменения величины по отношению к другой, в то время как неопределенный интеграл представляет кривую. Она распложена в параллельном направлении, а также имеет касательные во время пересечения неровных линий с иными, ортогональными к оси, представляющей переменную.
Методы сложения
Если вы столкнулись с проблемой, как применяется суммирование для математических операций дифференцирования интегрирования, следует тщательно ознакомиться с основными формулами. Они являются аксиомой в обучении, потому используются повсеместно. Обратите внимание, во время применения на собственных примерах, формулы верны, только если начинаются с i = 1.
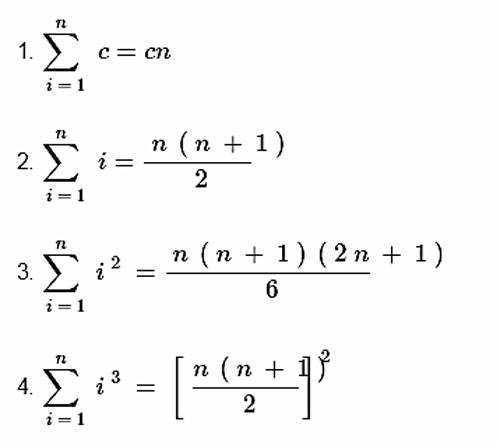
Решение «по частям»
Порой функция требует нестандартного подхода, чтобы добраться до конечного результата и удовлетворить условиям равенства. Почленное интегрирование и дифференцирование рядов основано на идентичности, которая выражается: ∫ f(x) g’(x) dx = f (x) g(x) - ∫ f’(x) g(x) dx
Алгоритм рассматриваемой методики, выглядит следующим образом:
- Выразить интегрированную функцию как произведение двух выражений. Обозначим одно из них f (x), другое g′ (x).
- Теперь приступить к выявлению двух других формул, которые возможно применить при выполнении первого пункта. Ряд изменится. Дифференцированием преобразуем f ′(x), чтобы получить выражения f (x). Приступаем к другой части - g (x) интегрируется в g′(x). При этом, dx остается в изначальной форме и не используется.
- Вставьте полученные выражения в формулу по частям. На этом процедура заканчивается, и теперь вы можете попытаться оценить новый интеграл справа, поскольку он стал значительно проще для понимания.
Ранее данные метод задействовал интегрирования по частям с помощью матрицы. Способ увенчался успехом, но занимал много времени, потому в настоящее время он применяется реже, в особых случаях, когда решение практически невозможно найти. Для этого достаточно поместить f и g′ в первую строку и вычислить f ′ и g во второй.
Зачем нужна интеграция по частям?
Ситуации случаются разные. Порой решения оказываются куда сложнее, чем на первый взгляд. Потому следует выделить основные проблемы, нередко встречающиеся при почленном интегрировании и дифференцировании степенных рядов. Рассмотрим два основных правила.
Во-первых, ту часть, которую мы намереваемся интегрировать, то есть выбранную для g ′(x), мы должны иметь возможность преобразовать. Сделать это важно максимально быстро. Дело в том, что сложное интегрирование для g редко приводит к улучшенному интегралу, повышая сложность. Все это негативно сказывается на свободе наших действий во время решений, а также зависит от степеней, синусов и косинусов. Пусть поиск правильного ответа займет время, но приведет к правильному, нежели запутанному.
Во-вторых, все остальное, то есть часть, которую мы намерены дифференцировать и обозначим F, должна заметно выделиться после преобразования. После несложной процедуры мы заметим, что новый интеграл окажется более упрощенным, чем предшественник.
Так, когда мы объединяем два правила и используем его при решении, то получаем возможность воспользоваться дифференцированием и интегрированием степенных функций, которые имеет смысл рассматривать по частям.
Существует и способ удаление x, позволяющий эффективно задействовать преобразования в различных ситуациях. Например, мы можем легко интегрировать, умножив функцию на полином, который мы сокращаем с помощью дифференцирования.
∫ x2 sin(3x) dx
∫ x7 cos(x) dx
∫x4 e4x dx
В качестве f мы берем степень x (в более общем случае - многочлен), а также используем g’. Очевидно, что каждое дифференцирование уменьшает степень числа на единицу, потому, если в примере она достаточно высокая – примените почленное интегрирование несколько раз. Это поможет сократить время.
Сложность некоторых уравнений
В данном случае речь идет о дифференцировании и интегрировании степенных рядов. Функцию можно рассматривать так, как будто x – является областью интервала сходимости точек. Правда метод подойдет далеко не всем. Дело в том, что любые функции могут быть выражены в виде степенных рядов, преобразовываясь в линейную структуру и наоборот.
Например, дано ex. Мы может выразить его в качестве уравнения, которое на самом деле является просто бесконечным полиномом. Степенной ряд легко заметить, вычислив, но он не всегда эффективен.
Определенный интеграл как предел суммы
Посмотрите на следующее графическое интегрирование и дифференцирование.
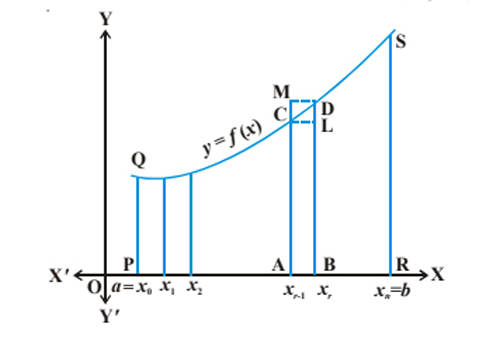
Для того чтобы легко понимать сложную функцию, достаточно тщательно разобраться в ней. Оценим область PRSQP между кривой у = f (x), осью х и координатами «x = а» и «x = b». Теперь разделите интервал [а, b] на 'n' равных подинтервалов, обозначенных следующим образом: [x0 , x1 ], [x1 , x2 ], [x2 , x3 ]…. [xn - 1 , xn ].
Где x0 = a, x1 = a + h, x2 = a + 2h, x3 = a + 3h… .. xr = a + rh и xn = b = a + nh или n = (b - a) / h. (1). Отметим, что при n → ∞ h → 0.
Рассматриваемое пространство PRSQP является суммой всех «n» подобластей, где каждая определена на определенной посредственности [хr-1 , хr ], r = 1, 2, 3… n. При правильном подходе, данные функции можно подвергнуть дифференцированию и интегрированию для быстрого решения.
Теперь посмотрите на ABDM на рисунке. На его основе целесообразно сделать следующее наблюдение о площадях: (ABLC) < (ABDCA) < (ABDM).
Также отметим, что при h → 0 или хr - хr-1 → 0 все три области становятся практически равными друг другу. Следовательно, мы имеем:
sn = h [f(x0) + f(x1) + f(x2) + …. f(xn – 1)] = h r=0∑n–1 f(xr) (2)
или Sn = h [f(x1) + f(x2) + f(x3) + …. f(xn)] = h r=1∑n f(xr) (3)
В данном случае sn и Sn обозначают сумму площадей всех нижних и верхних прямоугольников, поднятых над интервалами [хr–1, хr] для r = 1, 2, 3,…, n соответственно. Чтобы представить это в перспективе, уравнение (1) можно переписать в виде:
sn < площадь области (PRSQP) < Sn … (4)
Кроме того, предполагается, что предельные значения (2) и (3) одинаковы в обоих случаях, и общим является лишь площадь под кривой. В итоге мы имеем:
limn → ∞ Sn = limn → ∞ sn = области PRSQP = ∫ab f(x) dx … (5)
Площадь также является предельным значением пространства, которое находится между прямоугольниками ниже кривой и над кривой. Для удобства следует обратить внимание на высотку фигуры, равную кривой на левом краю каждого подинтервала. Следовательно, уравнение переписывается в конечный вариант:
∫ab f(x) dx = limn → ∞ h [f(a) + f(a + h) + …. + f(a + {n – 1}h)]
или ∫ab f(x) dx = (b – a) limn → ∞ (1/n) [f(a) + f(a + h) + …. + f(a + {n – 1}h)]
Заключение
Дифференцирование и интегрирование отличается между собой рядом свойств, формул и противоположными изменениями. Одно не может преобразоваться в другое без помощи. Если дифференциация помогает найти производную, то интеграция выполняет совершенно другое действие. Она добавляет некоторые части, способна помочь со степенями, сокращая их или усовершенствовать пример, упростив.
Также она применяется для проверки дифференцированных уравнений. Иначе говоря – они действуют, как единое целое, что не могут сосуществовать раздельно, поскольку дополняют друг друга. Применяя правила, зная множество методик, теперь вы гарантированно решите сложные задачи.


























