Обратные числа - фундаментальное понятие математики, без которого невозможно представить современную алгебру, анализ и другие разделы. Давайте разберемся, что это такое и почему они так важны.
Определение и свойства обратных чисел
Обратные числа - это числа, которые при перемножении дают в результате единицу. Например, число 3 и число 1/3 являются обратными, так как 3 * (1/3) = 1.
Формальное определение:
Числа a и b называются обратными или взаимно обратными, если выполняется равенство:
a * b = 1
Где 1 - это число-единица.
Геометрическая интерпретация
Есть простая геометрическая интерпретация обратных чисел. Рассмотрим числа как масштабные коэффициенты. Например, если числа являются коэффициентами подобия для двух фигур. Тогда обратные числа соответствуют фигурам с обратным масштабом.
Например, если одна фигура в 3 раза больше другой, то вторая фигура в 3 раза меньше первой. Отсюда числа 3 и 1/3 являются обратными в этом смысле. Их произведение (масштаб подобия туда и обратно) равно 1.
Обратные числа и деление
Обратные числа тесно связаны с операцией деления. Важное свойство:
- Деление числа a на число b равносильно умножению числа a на обратное число к b:
a / b = a * (1 / b)
Поэтому знание обратного числа позволяет выполнить деление, не используя саму операцию деления. Это очень удобно при работе со сложными математическими объектами.
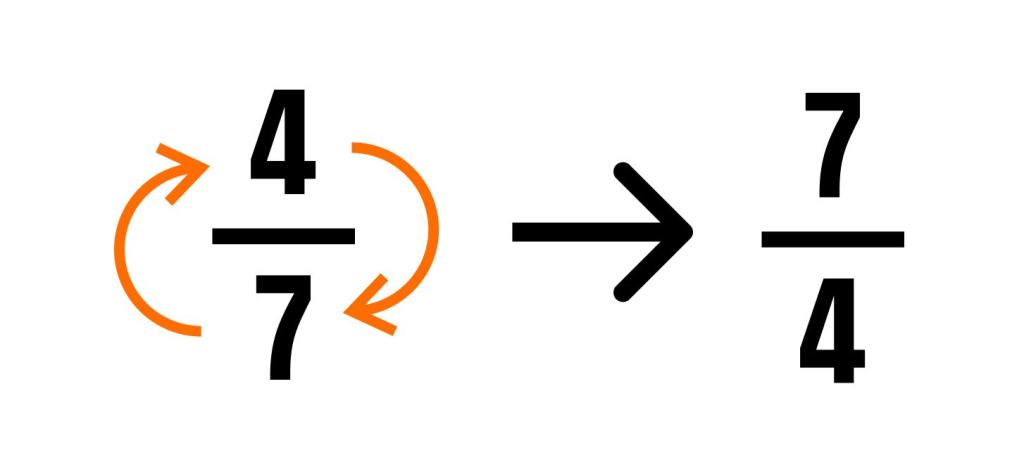
Свойства обратных чисел
Рассмотрим основные свойства обратных чисел:
-
Произведение любой пары обратных чисел равно 1. Это следует из определения.
-
Сумма двух положительных обратных чисел не меньше 2. Математически:
если
a > 0иb = 1/a, тоa + b >= 2
Это интересное и важное свойство обратных чисел, которое часто используется при доказательстве неравенств и в других задачах.
Зачем нужны обратные числа
Итак, мы выяснили, что такое обратные числа и каковы их основные свойства. Но зачем они нужны на практике? Дело в том, что обратные числа являются мощным инструментом во многих областях математики и ее приложениях.
Решение уравнений
Одно из основных применений обратных чисел - это решение различных уравнений. Например, рассмотрим простейшее линейное уравнение:
5x = 2

Чтобы найти x, нам нужно разделить обе части уравнения на 5. Но вместо деления, можно умножить обе части на обратные числа к 5, то есть на 1/5:
5x * (1/5) = 2 * (1/5)
В результате получаем:
x = 2/5
Как видите, использование обратного числа позволило избежать деления и значительно упростить решение.
Нахождение значений обратных функций
Еще одно важное применение - это вычисление значений так называемых обратных функций. Рассмотрим функцию y = 2x + 1. Обратная к ней функция записывается как x = f^-1(y).
Чтобы найти значение обратной функции в точке y = 5, мы можем воспользоваться обратными числами:
- Приравниваем y = 5 в исходном уравнении:
- 5 = 2x + 1
- Решаем это уравнение относительно x:
- 2x = 4
- Умножаем обе части на обратное число к 2, то есть на 1/2:
- x = 2
Получаем, что значение обратной функции в точке 5 равно 2. Как видите, и здесь обратные числа сильно упрощают все вычисления.





















