Теорема Вейерштрасса является одним из основополагающих утверждений математического анализа. Она позволяет изучать свойства непрерывных функций на компактных множествах и играет ключевую роль во многих разделах современной математики.
Эта теорема была доказана в XIX веке немецким математиком Карлом Вейерштрассом. Несмотря на ее значимость, по мнению некоторых историков науки, вклад Вейерштрасса до сих пор недооценен по сравнению с достижениями других выдающихся математиков того времени.
В данной статье мы попытаемся разобраться, насколько справедливы эти утверждения. Рассмотрим историю открытия теоремы Вейерштрасса, ее формулировку и следствия. Обсудим значение этого результата для математики и возможности его дальнейшего применения.
Обстоятельства открытия теоремы Вейерштрасса
Карл Вейерштрасс был одним из величайших математиков XIX века. Он внес фундаментальный вклад в развитие математического анализа, теории функций и топологии. Среди его многочисленных достижений особое место занимает теорема о существовании предела для монотонной ограниченной последовательности, названная в его честь теоремой Вейерштрасса.
Вейерштрасс открыл эту теорему в середине XIX века, когда активно занимался исследованиями в области последовательностей и рядов. До него уже были известны некоторые частные случаи этой теоремы, однако всеобъемлющей формулировки еще не существовало.
Вейерштрасс дал строгое математическое доказательство того факта, что любая монотонная и ограниченная последовательность имеет предел. Этот результат лег в основу современной теории пределов и послужил мощным импульсом для дальнейшего развития математического анализа.

Формулировка и следствия теоремы Вейерштрасса
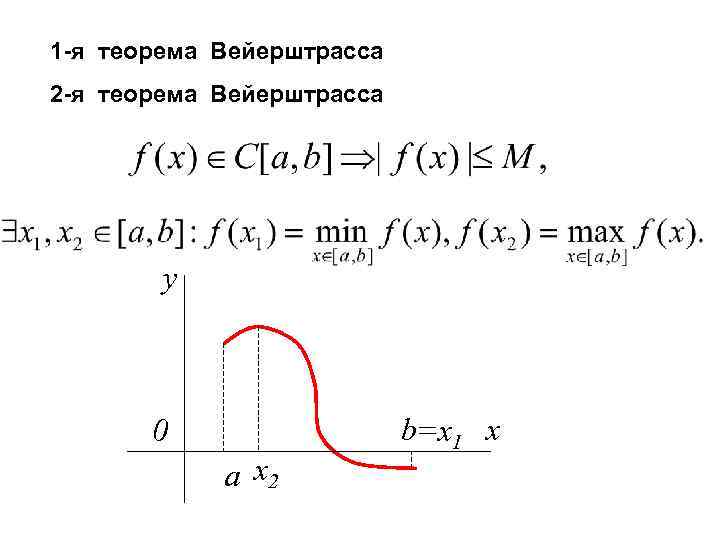
Теорема Вейерштрасса утверждает, что любая непрерывная функция на компактном множестве достигает своей верхней и нижней грани. В частности, для функции, определенной на замкнутом ограниченном интервале, это означает, что она достигает на этом интервале своего максимума и минимума. Формально теорема формулируется следующим образом:
- Пусть X - компактное метрическое пространство, f: X → R - непрерывная функция. Тогда существуют такие элементы x1, x2 ∈ X, что для любого x ∈ X выполняется:
- f(x1) ≤ f(x) ≤ f(x2).
Иными словами, непрерывная на компакте функция ограничена и достигает своих точных верхней и нижней граней. Это утверждение крайне важно в математическом анализе, поскольку позволяет изучать свойства функций на компактных множествах. Основные следствия теоремы Вейерштрасса:
- Любая непрерывная функция на отрезке достигает на нем своего максимума и минимума.
- Любой непрерывный функционал на нормированном пространстве достигает своей нормы на единичной сфере этого пространства.
Кроме того, на основе теоремы Вейерштрасса строятся доказательства существования решения в задачах вариационного исчисления. Таким образом, значение этой теоремы для математического анализа трудно переоценить.
Значение теоремы Вейерштрасса для развития математики
Теорема Вейерштрасса, доказанная в 1875 году, стала одной из фундаментальных теорем математического анализа. Она позволила значительно расширить класс функций, для которых можно было доказывать важные свойства, такие как ограниченность, существование экстремумов и другие. До открытия этой теоремы многие результаты были доказаны лишь для алгебраических функций.
Благодаря теореме Вейерштрасса стало возможным изучать функции, заданные конструктивно или как решения дифференциальных уравнений. Это позволило получить фундаментальные результаты о непрерывных отображениях компактных метрических пространств, имеющих огромное значение в топологии, функциональном анализе и теории динамических систем.
Кроме того, на основе теоремы Вейерштрасса были построены теории интегрирования Римана и Лебега, без которых невозможно современное развитие математического анализа. В частности, интеграл Лебега опирается на представление интегрируемой функции как предела последовательности простых функций. Сходимость такой последовательности к оригинальной функции гарантируется благодаря теореме Вейерштрасса.
В теории уравнений с частными производными теорема Вейерштрасса лежит в основе доказательств существования классических и обобщенных решений. А в теории оптимального управления она используется для обоснования существования оптимального управления в задачах оптимизации различных функционалов.
Таким образом, теорема Вейерштрасса оказала огромное влияние на развитие практически всех разделов математического анализа в 20 веке. Многие фундаментальные результаты этой эпохи были бы невозможны без использования этой теоремы. Поэтому ее значение для математики трудно переоценить, и она по праву считается одной из величайших теорем математического анализа.
Перспективы дальнейшего изучения и применения теоремы Вейерштрасса
Несмотря на то, что теорема Вейерштрасса была доказана почти полтора века назад, она продолжает играть важную роль в современной математике и имеет большой потенциал для дальнейшего развития и применения.
Во-первых, активно ведутся исследования по расширению и уточнению этой теоремы. В частности, изучаются возможности ее обобщения на случай топологических и упорядоченных векторных пространств. Также рассматриваются различные варианты усиления условий теоремы и доказательства более точных оценок границ изменения функций.
Во-вторых, теорема Вейерштрасса продолжает активно использоваться в классическом математическом анализе. Различные ее модификации и обобщения позволяют доказывать важные теоремы, например, о существовании и единственности решений дифференциальных уравнений, уравнений математической физики и других задач, где требуется применение нетривиального анализа.

























