В предложенной работе будет подробно рассмотрен вопрос преобразования логических выражений. Кроме этого, предлагаем вам пройти краткий курс по логике, где будут рассматриваться основные законы и понятия. Преобразование логических выражений – это довольно непростой процесс, если не ознакомиться со всеми нюансами самого предмета.
Курс информатики будет казаться простым и доставлять удовольствие, если внимательно прочитать данную статью и ознакомиться с правилами и законами преобразования, решения задач и составления схем. Предлагаем приступить прямо сейчас.
Наука логика

Основы логики – это довольно непростой предмет, по нему написано очень много томов. В данной статье будут рассмотрены азы и законы преобразования логических выражений, то есть информация будет максимально сжатой и концентрированной. Это необходимо для рассмотрения более осмысленно компьютерных технологий и построения схем.
Для начала что такое логика и зачем она нужна? Важно отметить, что это целая наука, которая рассматривает формы и способы рассуждения. Все, что мы видим, слышим или делаем, подчиняется законам. Бросили мяч с высоты - он обязательно летит вниз, так как подчиняется законам физики. Завариваем утром ароматный кофе, добавляем сахар, а сыпучие вещества моментально растворяются в воде, подчиняясь законам физики. Мы ведем беседу с друзьями, делимся своими планами: «Если я хорошо защищу работу, то получу красный диплом», «У меня не получится приехать на машине, так как она находится в ремонте». Не замечая, мы строим все наши разговоры, опираясь именно на логику и ее законы. Так зачем нужна наука логика? Конечно, зная ее законы, вы сможете безошибочно определять исход какого-либо события, так как не придется действовать наугад и рисковать.
Хоть мышление является довольно сложным процессом, тем не менее можно его разделить на некие составляющие, точнее, формы (с помощью чего происходит выражение мысли):
- понятия;
- высказывания;
- умозаключения;
- доказательства.
Далее предлагаем вам перейти к логическим функциям и преобразованию логических выражений. Информатика окажется для вас веселым и довольно простым предметом, если внимательно читать данную статью.
Логические функции

Сейчас мы предлагаем познакомиться с логическими функциями. Часто в билетах единого государственного экзамена в части В попадаются задачи на преобразование логических выражений в числовых отрезках. Их невозможно решить без знания функций логики.
Какова основная задача данной науки? Конечно, изучение логических выражений (как сложных, так и простых). Как получается сложное высказывание? Путем слияния простых, что происходит благодаря связкам, которые принято называть функциями.
Всего можно выделить пять связок:
- инверсия (то есть отрицание, при помощи данной функции можно получить высказывание, обратное данному: я сегодня иду в кино – я сегодня не иду в кино);
- дизъюнкция (эту функцию часто называют логическим сложением, для того чтобы стало понятно, приведем простой пример из жизни: «если у меня будет болеть голова или живот, то я не пойду в школу» - это выражение будет истинным, если учтено хоть одно из требований);
- конъюнкция (часто называют логическим умножением: «если я помою посуду и сделаю уроки, то пойду гулять с друзьями» - это выражение будет истинным, если будут учтены два условия);
- импликация (в логике эту функцию называют следованием, к сожалению, ее нельзя проиллюстрировать жизненной ситуацией; ложной функция будет в том случае, если что-то хотели сделать, но не получилось, в остальных случаях функция будет истинной);
- эквиваленция (или равенство, если два высказывания истинны или ложны, то в результате мы получаем истину).
Важно отметить, что в информатике любое простое выражение обозначается заглавной буквой латинского алфавита. Далее нужно обязательно запомнить таблицу истинности к каждой функции. Обратите внимание на то, что заучивать ее не обязательно, довольно будет только понимания функций.
Таблицы истинности
Конъюнкция
Первое выражение (А) | Второе выражение (В) | Результат (С) |
Л | Л | Л |
И | Л | Л |
Л | И | Л |
И | И | И |
Дизъюнкция
А | В | С |
Л | Л | Л |
И | Л | И |
Л | И | И |
И | И | И |
Инверсия
А | В |
И | Л |
Л | И |
Импликация
А | В | С |
Л | Л | И |
И | Л | Л |
Л | И | И |
И | И | И |
Эквиваленция
А | В | С |
Л | Л | И |
И | Л | Л |
Л | И | Л |
И | И | И |
Кроме этого, важно отметить и тот факт, что ложь в логике обозначается цифрой 0, а истинное выражение - цифрой 1. Для своего удобства можно применять и знаки плюса и минуса. Обратите свое внимание на то, что ложные и истинные выражения в предложенных таблицах обозначены буквами "Л" и "И" соответственно.
Построение
Перед тем как переходить к преобразованию логических выражений, необходимо познакомиться с самим их построением. Любое составное или, как было сказано раньше, сложное выражение состоит из двух частей:
- переменные, которые обозначаются большими буквами латинского алфавита;
- знаки, которые обозначают функцию и соединяют простые выражения между собой.
Как составить выражение на языке алгебры логики? Для этого нужно сделать несколько вещей:
- разделить все высказывание на простые выражения;
- обозначить эти элементы буквами;
- выделить связи между простыми выражениями;
- записать получившееся выражение с помощью специальных символов алгебры логики.
Предлагаем рассмотреть простой пример: (Z*F=5 или Z*F=4) И (Z*F не равно 5 или Z*F не равно 4). Необходимо вместо переменных подставить 2. После этого мы получаем выражение (4=5 или 4=4) и (4 не равно 5 или 4 не равно 4). После проведенных операций мы должны выделить выражения и связи между ними, должно получиться следующим образом: (Z или F) и (не Z или не F). После этого нам необходимо преобразовать эту запись, подставив значения высказываний. В том случае, если выражение верное, то необходимо подставить 1, в противном случае – 0. Мы получаем: G=1 и 1. После необходимых вычислений мы получим результат: G=1, то есть сложное выражение является истинным.
Законы
Сейчас предлагаем вам рассмотреть законы логики и правила преобразования логических выражений. Важно упомянуть то, что любое логическое выражение может быть преобразовано в другое при помощи законов логики. Сейчас мы подробно рассмотрим все десять правил.
Первый в нашем списке – «закон двойного отрицания». То есть выражение «не (не А)» будет равняться выражению «А».
Коммуникативный закон есть и в математике, его запомнить довольно просто. А+В=В+А, А*В=В*А.
Сочетательный закон - (D+E)+F=(D+F)+E, тот же закон применим и к логическому умножению.
Распределительный закон – это элементарное открытие скобок. Пример: (А+В)*С=(А*С)+(В*С).
Закон де Моргана: не(А+В)=неА*неВ, не(А*В)=неА+неВ, АимпликацияВ=неА+В, не(АимпликацияВ)=А*неВ.
Идемпотентность: Х+Х=Х или С*С=С.
Исключение констант: Х+1=1, Х+0=Х; Х*1=Х, Х*0=0.
Следующим мы выделим закон противоречия, следуя ему, можно утверждать следующее равенство: В*неВ=0.
В логике есть и закон поглощения, который на практике выглядит следующим образом: С+(С*D)=С или С*(С+D)=С.
Так же важно для преобразования логических выражений запомнить закон исключения: (С*Е)+(неС*Е)=Е или (С+Е)*(неС+Е)=Е.
Если подробно рассмотреть и запомнить все представленные в данном разделе законы, то проблем с преобразованием никогда не возникнет. Не менее важен и порядок выполнения функций. Уделяйте этому пункту больше внимания, правильное распределение порядка функций – это залог правильного решения задачи.
Правила и законы преобразования и упрощения, порядок выполнения действий с примерами
Логические законы и правила преобразования логических выражений очень просты для запоминания. Если вы сомневаетесь в правдивости хоть одного из них, то проверьте самостоятельно. Для этого необходимо потратить 10 минут своего времени и составить таблицы истинности для получения ответа.
Сейчас предлагаем рассмотреть логические законы и правила преобразования логических выражений на конкретных примерах. Это необходимо для того, чтобы как следует закрепить полученные знания. Обратите особое внимание на очередность действий.
Нам дано: С+(неС*Е). Необходимо упростить выражение. Первым делом предлагаем раскрыть скобки. Тогда мы получаем выражение: (С+неС)*(С+Е). Отметим сразу, что логическое сложение двух противоположных высказываний дает нам истину. Что получаем в итоге: 1*(С+Е). Опять открываем скобки: (1*С)+(1+Е). Сейчас еще раз вспоминаем законы и получаем ответ: С+Е.
Как вы уже увидели, все достаточно просто. Для решения таких задач необходимо запомнить законы, которые были перечислены в прошлом разделе. Предлагаем переходить к решению логических задач, так как это задание уже немного сложнее предыдущего.
Решение задач
Мы познакомились с азами науки под названием «логика», преобразование логических выражений мы коротко рассмотрели, законы перечислили. Наиболее сложные задания с составлением логических выражений – это задачи. Важно отметить, что они могут решаться с помощью рассуждения, преобразования выражения или табличным методом. Предлагаем рассмотреть одну из них подробно.

Три мальчика (Кирилл, Антон и Костя) находились в одной комнате. Вдруг мама из кухни слышит звук разбитой чашки. Прибежала к сыновьям и спросила: "Кто это сделал?" Ответ был следующим: Кирилл сказал, что чашку разбил не Костя, а Антон; Антон сказал, что это сделал Костя, а не Кирилл; Костя утверждает, что виновником не является Антон. Нам известно, что кто-то один из мальчиков сказал маме неправду. Нужно выяснить, кто разбил чашку.
Если рассуждать логически, то ответы Кирилла и Антона противоречат друг другу, так же, как и Кирилла с Костей. Следовательно, они не могут быть оба правдивыми. Делаем следующее умозаключение - Антон и Костя сказали правду, а Кирилл является виновником разбитой чашки. Это был применен метод размышления. Сейчас просмотрим решение этой же задачи, только при помощи метода преобразования выражения. Для начала введем сокращения:
- КР – чашка разбита Кириллом;
- А – чашка разбита Антоном;
- К – виновник Костя.
Ответы мальчиков:
- Кирилл – неК, А;
- Антон – неКР, К;
- Костя – неА.
Предлагаем составить выражение, если Костя солгал, а Кирилл и Антон сказали правду: неК*А=1 и К*неКР=1 и А=1. Преобразовывая выражение, мы получаем противоречие: 0=1. Наше предположение неверно, стоит проверить другие предположения.
Если мы предполагаем, что Кирилл солгал, а Антон и Костя сказали маме правду, то получаем следующее выражение: К*неА=1 и К*неКР=1 и неА=1. Упростив выражение, мы получаем КР*неА*неК=1. Это говорит о том, что наше предположение было верным, действительно, Кирилл разбил чашку и солгал маме.
Табличный метод решения
Рассмотренные законы логики и преобразование логических выражений, безусловно, помогли нам справиться с задачей, которая представлена в предыдущем разделе. Сейчас предлагаем рассмотреть табличный метод решения на следующей задаче.
Дмитрий, Анатолий и Людмила являются поклонниками почтовой переписки, нам известно, что все живут в разных частях света и имеют разное хобби. Определите, кто живет в каком городе и чем увлекается. Известны следующие факты:
- Дмитрий никогда не бывал в Париже, а Людмила - в Риме;
- тот, кто живет в Париже, не любит кино;
- человек, который живет в Риме, занимается вокалом;
- Людмила испытывает отвращение к балету.
Для того чтобы решить задачу, нужно составить небольшую таблицу.
Франция | Италия | США | Вокал | Балет | Кино | |
Дмитрий | ||||||
Анатолий | ||||||
Людмила |
Далее от вас требуется максимум внимания. Все, что вы прочитали в условии, должно отразиться в этой таблице. По ходу заполнения станет ясно следующее:
- Дмитрий живет в Риме и занимается вокалом;
- Анатолий живет в Париже и часто посещает балет;
- Людмила – это большая поклонница киноискусства, которая проживает в США.
Обратите еще раз свое внимание на то, что истинное выражение отмечается цифрой 1, а ложное – 0. Заполняя таблицу данными символами, вы быстро найдете ответ на вопрос, который вас интересует.
Микросхематика
Примеры преобразования логических выражений, которые мы рассмотрели, являются довольно сложными на первый взгляд. В билетах единого государственного экзамена условие может вовсе даваться в виде микросхемы.
Важно знать, что все цифровые устройства основываются на логических элементах, то есть неких устройствах, которые выполняют одну логическую функцию.
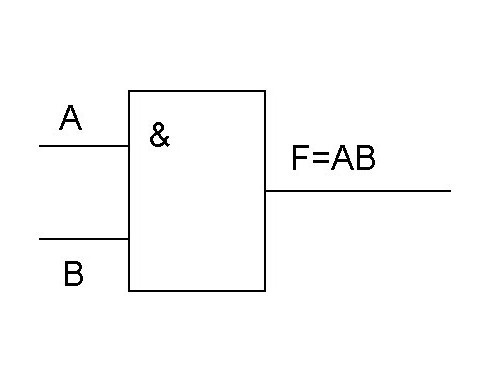
Мы уже говорили о такой функции, как конъюнкция (логическое умножение). Его принято обозначать символом &. Эта функция необходима для конъюнкции нескольких значений. На картинке вы видите схему логического умножения.
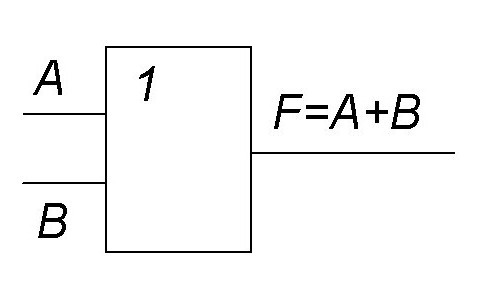
Функция дизъюнкция необходима для реализации дизъюнкции некоторых входных значений. При записи выражения эту функцию принято обозначать символом Ú. На картинке представлена схема.
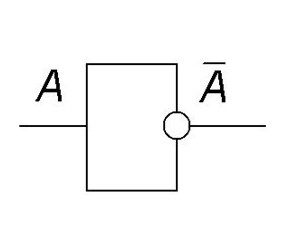
Функция инверсии служит преобразователем одного выражения в противоположное. На рисунке вы видите, как выглядит схема «не».
Пример упрощения формулы №1
Рассмотренные правила преобразования логических выражений необходимо закрепить на практике. Именно преследуя эту цель, мы предлагаем решить самостоятельно два примера средней сложности и сопоставить с результатами в данном разделе статьи.
Если вы еще не успели запомнить формулы преобразования логических выражений, то можете сделать себе небольшую «напоминалку». Вы увидите, что вскоре вы не будете в нее подсматривать.
Пример: (Х+Т)*(неХ+Т)*(М+неТ). Не стоит слепо списывать, попробуйте решить пример самостоятельно.
В ходе упрощения мы получаем следующие записи: Т*(М+неТ)=(Т*М)+(Т*неТ)=(Т*неМ)+0=(Т+0)*(М+0)=Т*М.
Как видите, из довольно длинного и громоздкого сложного выражения мы получили короткое Т*М. Если у вас не получилось решить самостоятельно данный пример, то обратитесь еще раз в пункт, где мы рассматривали преобразование логических выражений, задачи.
Пример упрощения формулы №2

В данном разделе предлагаем вам упростить выражение (Е+Н)*(Е+К). Разберем решение поэтапно. Первым делом нам необходимо раскрыть скобки, вспоминаем курс начальной математики. В результате мы получаем следующее выражение: Е*Е+Е*К+Н*Е+Н*К. Далее мы замечаем, что в полученном выражении есть часть Е*Е, вспоминаем закон идемпотентности и преобразовываем запись: Е+Е*К+Н*Е+Н*К. Следующим этапом преобразуем часть Е+Е*К, воспользовавшись вынесением за скобки переменной Е и свойством: А+1=1. Мы получаем выражение: Е+Н*Е+Н*К. Следуем аналогично последнему пункту и выносим за скобки Е. В результате мы получаем ответ: Е+Н*К.
Обратите свое внимание на то, что задания только кажутся сложными на первый взгляд. Чтобы «щелкать их, как семечки», необходимо просто выучить основные законы логики.


























