Ложное и истинное высказывание часто употребляется в языковой практике. Первая оценка воспринимается как отрицание истинности (неистинности). В реальности используют и иные виды оценки: неопределенность, недоказуемость (доказуемость), неразрешимость. Рассуждая над тем, для какого числа x истинно высказывание, необходимо рассмотреть законы логики.
Возникновение «многозначной логики» привело к использованию неограниченного числа показателей истинности. Ситуация с элементами истинности запутана, усложнена, поэтому важно внести в нее ясность.
Принципы теории
Истинное высказывание – это значение свойства (признака), рассматривается всегда для определенного действия. Что такое истина? Схема следующая: «Высказывание Х обладает значением истинности Y в том случае, когда истинно высказывание Z».
Давайте рассмотрим пример. Нужно понять, для какого из приведенных истинно высказывание: «Предмет а имеет признак В». Это высказывание неверно в том, что у предмета есть признак В, и неверно в том, что а не обладает признаком в». Термин «неверно» в данном случае употребляется в качестве внешнего отрицания.

Определение истинности
Как определяется истинное высказывание? Вне зависимости от структуры высказывания Х допускается только следующее определение: «Высказывание Х истинно тогда, когда есть Х, только Х».
Данное определение дает возможность ввести в язык термин «истинно». Оно определяет акт принятия согласия или высказывания с тем, о чем говорится в нем.
Простые высказывания
В них истинное высказывание без определения. Можно ограничиться при высказывании «Не-Х» общим определением, если это высказывание не является истинным. Истинна конъюнкция "X и Y", если будут истинны X и Y.

Пример высказывания
Как понять, для каких x истинно высказывание? Чтобы ответить на этот вопрос, используем выражение: «Частица а находится в области пространства b». Рассмотрим для этого высказывания следующие случаи:
- невозможно наблюдать частицу;
- можно наблюдать частицу.
Второй вариант предполагает определенные возможности:
- частица реально находится в определенной области пространства;
- ее нет в предполагаемой части пространства;
- частица движется так, что сложно определить область ее расположения.
В данном случае можно использовать четыре термина значений истинности, которые соответствуют приведенным возможностям.
Для сложных структур уместно использование большего количества терминов. Это свидетельствует о неограниченности значений истинности. Для какого числа истинно высказывание, зависит от практической целесообразности.

Двузначности принцип
В соответствии с ним, любое высказывание либо ложно, либо истинно, то есть, характеризуется одним из двух вероятных истинностных значений – «ложно» и «истинно».
Данный принцип является основой классической логики, которую именуют двузначной теорией. Двузначности принцип использовался Аристотелем. Этот философ, рассуждая над тем, для какого числа х истинно высказывание, считал его неподходящим к тем высказываниям, которые касаются будущих случайных событий.
Он устанавливал логическую взаимосвязь между фатализмом и принципом двузначности, положением о предопределенности любых действий человека.
В последующие исторические эпохи ограничения, которые накладывались на данный принцип, объяснялись тем, что он существенно затрудняет анализ высказываний о планируемых событиях, а также о несуществующих (ненаблюдаемых) объектах.
Задумываясь о том, какие высказывания истинные, этим методом не всегда можно было найти однозначный ответ.
Появляющиеся сомнения в логических системах были развеяны только после того, как была разработана современная логика.
Чтобы понять, для какого из приведенных чисел истинно высказывание, подходит двухзначная логика.
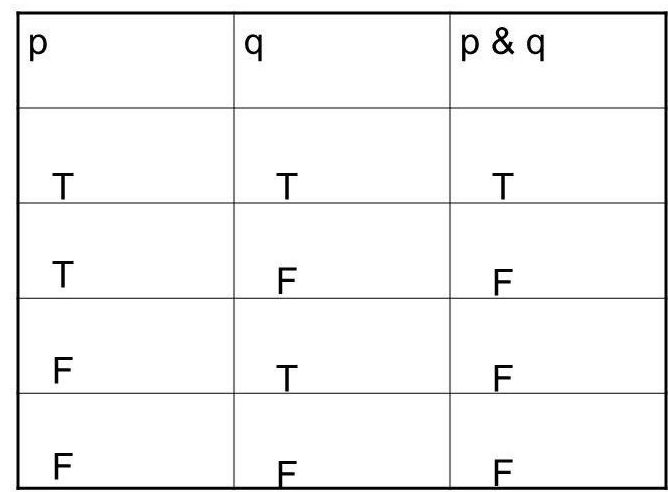
Принцип многозначности
Если переформулировать вариант двухзначного высказывания для выявления истинности, можно превратить его в частный случай многозначности: любое высказывание будет иметь одно п значение истинности, если п равно либо больше 2, или же меньше бесконечности.
В качестве исключений дополнительных значений истинности (выше «ложно» и «истинно») выступают многие логические системы, базирующиеся на принципе многозначности. Двузначная классическая логика характеризует типичные варианты использования некоторых логически знаков: «или», «и», «не».
Многозначная логика, претендующая на их конкретизацию, не должна противоречить результатам двузначной системы.
Ошибочным считают то убеждение, согласно которому, принцип двузначности всегда приводит к констатации фатализма и детерминизма. Также неверна и мысль, согласно которой, многократную логику рассматривают в качестве необходимого средства осуществления индетерминистических рассуждений, что принятие ее соответствует отказу от использования строгого детерминизма.

Семантика логических знаков
Чтобы понять, для какого числа Х истинно высказывание, можно вооружиться таблицами истинности. Семантика логическая представляет раздел металогики, который исследует отношение к обозначаемым объектам, их содержанию разнообразных языковых выражений.
Данная проблема рассматривалась уже в античном мире, но в виде полноценной самостоятельной дисциплины она была сформулирована только на рубеже XIX—XX веков. Работы Г. Фреге, Ч. Пирса, Р. Карнапа, С. Крипке позволили выявить суть данной теории, ее реалистичность и целесообразность.
На протяжении длительного временного периода семантическая логика опиралась в основном на анализ формализованных языков. Только в последнее время большая часть исследований стала посвящаться естественному языку.
В данной методике выделяют две основные области:
- теорию обозначения (референции);
- теорию смысла.
Первая предполагает исследование отношения разнообразных языковых выражений к обозначаемым объектам. В качестве ее основных категорий можно представить: «обозначение», «имя», «модель», «интерпретация». Данная теория является основой для доказательств в современной логике.
Теория смысла занимается поиском ответа на вопрос относительно того, что представляет собой смысл языкового выражения. Она объясняет их тождественность по смыслу.
Существенную роль теория смысла имеет при обсуждении семантических парадоксов, при решении которых любой критерий приемлемости считается важным и актуальным.

Логическое уравнение
Данный термин используется в метаязыке. Под логическим уравнением можно представить запись F1=F2, в которой F1и F2 являются формулами расширенного языка логических высказываний. Решить такое уравнение означает, определить те наборы истинных значений переменных, которые будут входить в одну из формул F1 либо F2, при которых будет соблюдаться предложенное равенство.
Знак равенства в математике в некоторых ситуациях свидетельствует о равенстве исходных объектов, а в ряде случаев он ставится для демонстрации равенства их значений. Запись F1=F2 может свидетельствовать о том, что речь идет об одной и той же формуле.
В литературе довольно часто под формальной логикой подразумевают такой синоним, как «язык логических высказываний». В качестве «правильных слов» выступают формулы, служащие семантическими единицами, используемыми для построения рассуждений в неформальной (философской) логике.
Высказывание выступает в качестве предложения, которое выражает конкретное суждение. Иными словами, оно выражает мысль о присутствии некоего положения дел.
Любое высказывание можно будет считать истинным в том случае, когда положение дел, описываемое в нем, существует в реальности. В иных случаях такое высказывание будет являться ложным утверждением.
Данный факт стал основой пропозициональной логики. Существует подразделение высказываний на простые и сложные группы.
При формализации простых вариантов высказываний применяют элементарные формулы языка нулевого порядка. Описание сложных высказываний возможно только с применением формул языка.
Логические связки необходимы для обозначения союзов. При их применении простые высказывания превращаются в сложные виды:
- «не»,
- «неверно, что…»,
- «или».
Заключение
Формальная логика помогает выяснять, для какого имени истинно высказывание, предполагает конструирование и анализ правил преобразования определенных выражений, которые сохраняют их истинное значение независимо от содержания. В качестве отдельного раздела философской науки она появилась только в конце девятнадцатого века. Вторым направлением является неформальная логика.
Основной задачей этой науки является систематизация правил, которые позволяют выводить новые утверждения на основе доказанных утверждений.
Фундаментом логики является возможность получения каких-то идей в качестве логического следствия иных утверждений.
Подобный факт позволяет адекватно описывать не только определенную проблему в математической науке, но и переносить логику в художественное творчество.
Логическое исследование предполагает отношение, которое существует между посылками и заключениями, выводимыми из них.
Его можно отнести к числу исходных, фундаментальных понятий современной логики, которую часто именуют наукой «что из него следует».
Сложно представить себе без подобных рассуждений доказательство теорем в геометрии, объяснение физических явлений, пояснение механизмов протекания реакций в химии.



























