Линейная функция - это прямая, проведенная по поверхности. Она может делиться на различные виды и модели. Ниже будут рассмотрены формулы ее получения, а также достижения ее совершенства в плоскости. На рисунках можно будет полностью в этом убедиться и понять, как она должна выглядеть.
Линейная функция y = kx + b
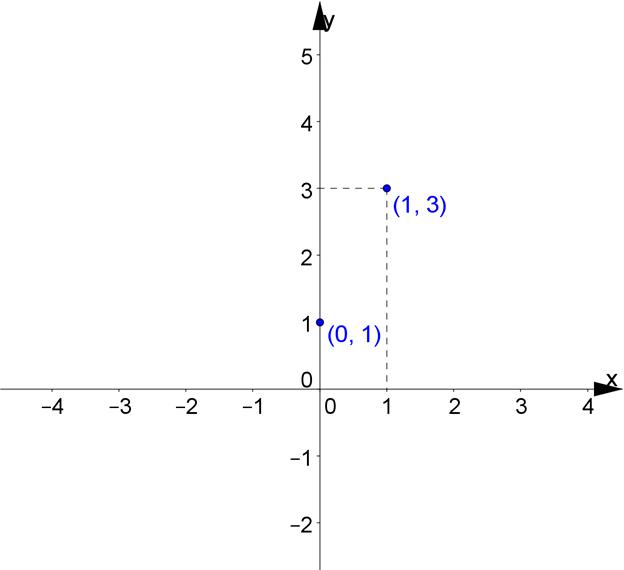
Это значение является точным показателем переменной в одном виде. Приращение относится к основному свойству линейной функции, оно становится пропорциональным приращенному аргументу. Иными словами - функция представляет обобщение прямой пропорциональности. Прямая - это график линейной функции. От этого и исходит ее название. Одна вещественная переменная касается другой вещественной функции.
Свойства
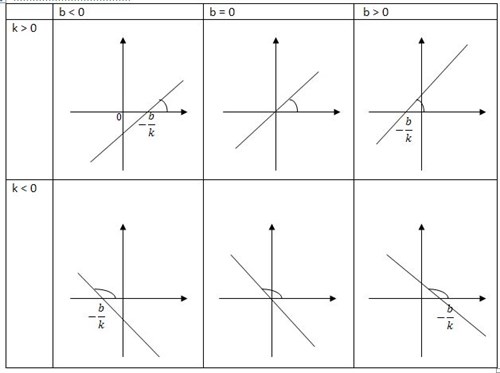
Линейная функция - это образующая прямая, у которой положительное направление оси абсцисс. Одним из ее определяющих угловых коэффициентов является к, он определяет тангенс угла а. Прямая, образованная в положительном направлении оси абсцисс, и является к. Другой координат b указывает координаты точек, а также пересечение прямой с осью.
Что представляют собой нелинейные функции?
Функции, которые не являются линейными, так и называются - нелинейными. Это математическое соотношение между переменными. Нелинейные нельзя выразить в виде y = ax + b. Этот термин используют в тех моментах, когда необходимо изучение общего случая. Начинается данный процесс с младших степеней. При этом рассматриваются квадратичные поправки. Такая функция обладает непрерывной кривизной.
Рассматриваемое нелинейное уравнение - произвольное. Примером нелинейной функции является у = х2. Часто применимы термины "линейная функция" с уточнением и добавлением "однородная". Она может быть применена для точного линейного отображения Х, что является векторным пространством. Линейная функция - это и есть вся система подобных ей.




















