Треугольник - двумерная фигура с тремя ребрами и таким же количеством вершин. Это одна из основных форм в геометрии. Объект имеет три угла, их суммарная градусная мера всегда равна 180°. Вершины принято обозначать латинскими буквами, например, ABC.
Теория
Треугольники можно классифицировать по разным признакам.
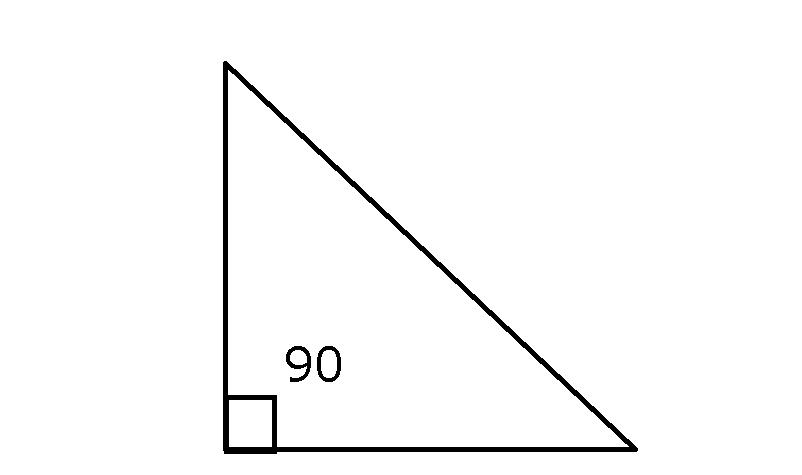
Если градусная мера всех его углов меньше 90 градусов, то его называют остроугольным, если один из них равен этому значению - прямоугольным, ну и в иных случаях - тупоугольным.
Когда треугольник имеет все стороны одинаковой величины, то именуют его равносторонним. На рисунке это отмечают перпендикулярной отрезку меткой. Углы в в таком случае всегда равны 60°.

Если же только две стороны треугольника равны, то его называют равнобедренным. В таком случае углы, находящиеся у основания, равны.
Треугольник, не подходящий под два предыдущих варианта, называют разносторонним.
Когда говорят, что два треугольника равны, это означает, что они имеют одинаковые размер и форму. Также они имеют одинаковые углы.
Если же совпадают исключительно градусные меры, то фигуры называют подобными. Тогда соотношение соответствующих сторон можно выразить определенным числом, которое называется коэффициентом пропорциональности.
Периметр треугольника через площадь или стороны
Как и в любом многоугольнике, периметр - это сумма длин всех сторон.
Для треугольника формула выглядит так: P = а + b + c, где a, b и c - длины сторон.
Существует еще один способ решения данной задачи. Он заключается в том, чтобы найти периметр треугольника через площадь. Для начала нужно знать уравнение, связывающее эти две величины.
S = p × r, где p - полупериметр, а r - радиус вписанной в объект окружности.
Весьма просто можно преобразовать уравнение в необходимый для нас вид. Получим:
p = S/r
Не забываем, что настощий периметр будет в 2 раз больше полученного.
P = 2S/r
Вот так просто решаются подобные примеры.




















