Определение цилиндра. Формула для объема. Решение задачи с латунным цилиндром

Пространственная геометрия, курс которой изучают в 10-11 классах школы, рассматривает свойства объемных фигур. В статье дается геометрическое определение цилиндра, приводится формула для вычисления его объема, а также решается физическая задача, где важно знать этот объем.

Что такое цилиндр?

С точки зрения стереометрии, определение цилиндру можно дать следующее: он представляет собой фигуру, образованную в результате параллельного перемещения прямого отрезка вдоль некоторой плоской замкнутой кривой. Названый отрезок не должен принадлежать той же плоскости, что и кривая. Если кривой является окружность, а отрезок перпендикулярен ей, то образованный описанным способом цилиндр называется прямым и круглым. Он показан на рисунке ниже.

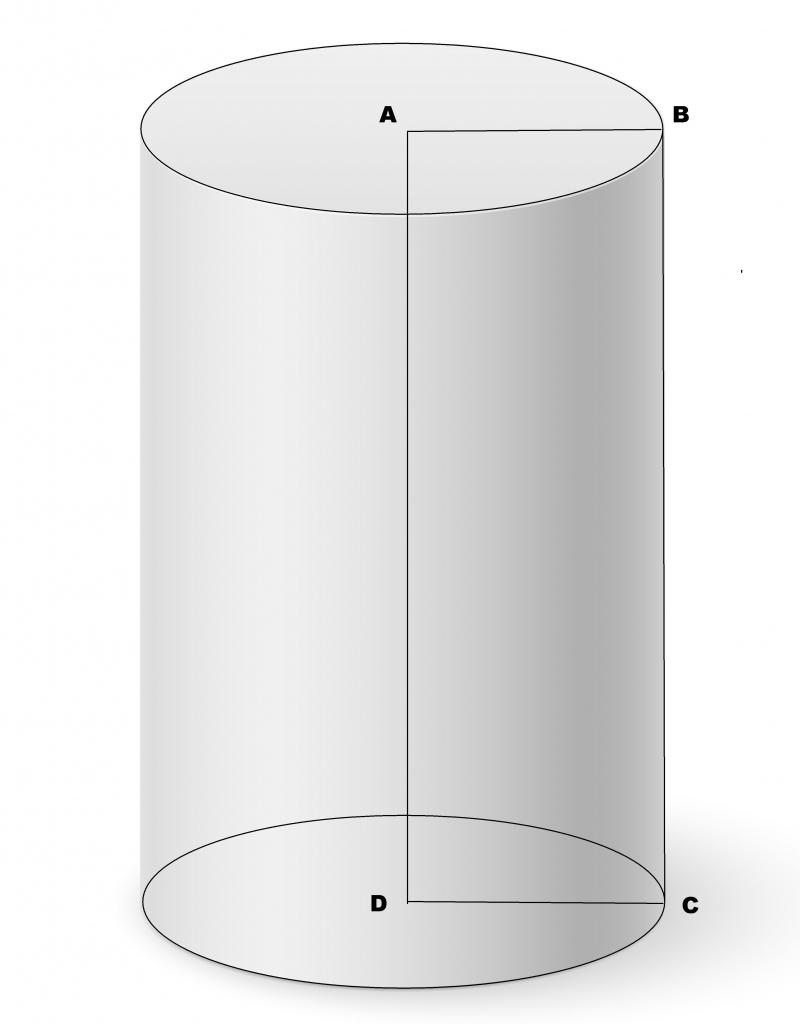
Не трудно догадаться, что эту фигуру можно получить, если вращать прямоугольник вокруг любой из его сторон.

Цилиндр имеет два одинаковых основания, которые являются кругами, и боковую цилиндрическую поверхность. Окружность основания называется директрисой, а перпендикулярный отрезок, соединяющий окружности разных оснований - это генератриса фигуры.

Как найти объем круглого прямого цилиндра?

Познакомившись с определением цилиндра, рассмотрим, какие параметры следует знать, чтобы математически описать его характеристики.

Расстояние между двумя основаниями - это высота фигуры. Очевидно, что она равна длине генератрисы. Будем обозначать высоту латинской буквой h. Радиус круга в основании обозначим буквой r. Он также называется радиусом цилиндра. Введенных двух параметров достаточно, чтобы однозначно описать все свойства рассматриваемой фигуры.

Учитывая геометрическое определение цилиндра, объем его можно вычислить по следующей формуле:

V = S*h

Здесь S - это площадь основания. Заметим, что для любого цилиндра и для всякой призмы справедлива записанная формула. Тем не менее для круглого прямого цилиндра ею пользоваться достаточно удобно, поскольку высота является генератрисой, а площадь S основания можно определить, вспомнив формулу для площади круга:

S = pi*r²

Таким образом, рабочая формула для объема V рассматриваемой фигуры запишется в виде:

V = pi*r²*h

Выталкивающая сила

Каждый школьник знает, что если какой-нибудь предмет погрузить в воду, то его вес станет меньше. Причиной этого факта является возникновение выталкивающей, или архимедовой силы. Она действует на любые тела, независимо от их формы и материала, из которого они изготовлены. Силу Архимеда можно определить по формуле:

F_A = ρ_l*g*V_l

Здесь ρ_l и V_l - плотность жидкости и вытесненный телом ее объем. Важно не путать этот объем с объемом тела. Они будут совпадать только в том случае, если тело полностью погружено в жидкость. При любом частичном его погружении V_l всегда меньше V тела.

Выталкивающей сила F_A называется потому, что она направлена вертикально вверх, то есть является противоположной по направлению силе тяжести. Разные направления векторов сил приводят к тому, что вес тела в любой жидкости меньше, чем на воздухе. Справедливости ради отметим, что в воздухе на все тела также действует выталкивающая сила, однако она пренебрежимо мала по сравнению с архимедовой силой в воде (меньше в 800 раз).

Разницу в весе тел в жидкости и в воздухе используют для определения плотностей твердых и жидких веществ. Этот метод получил название гидростатического взвешивания. Согласно легенде, впервые его применил Архимед для определения плотности металла, из которого была сделана корона.

Воспользуемся приведенной формулой для определения выталкивающей силы, действующей на цилиндр из латуни.

Задача на вычисление силы Архимеда, действующей на латунный цилиндр

Известно, что латунный цилиндр имеет высоту 20 см и диаметр 10 см. Чему будет равна архимедова сила, которая на него начнет действовать, если цилиндр бросить в дистиллированную воду.

Для определения выталкивающей силы на латунный цилиндр в первую очередь следует в таблице посмотреть плотность латуни. Она равна 8600 кг/м³ (это среднее значение ее плотности). Поскольку эта величина больше плотности воды (1000 кг/м³), то объект утонет.

Для определения силы Архимеда достаточно найти объем цилиндра, а затем воспользоваться приведенной формулой для F_A. Имеем:

V = pi*r²*h = 3,14*5²*20 = 1570 см³

В формулу мы подставили значение радиуса 5 см, так как он в два раза меньше данного в условии задачи диаметра.

Для выталкивающей силы получаем:

F_A = ρ_l*g*V = 1000*9,81*1570*10^-6 = 15,4 Н

Здесь мы перевели объем V в м³.

Таким образом, на цилиндр из латуни известных размеров, погруженный в воду, будет действовать направленная вверх сила 15,4 Н.