Понятие о призме. Формулы объема призм разного типа: правильной, прямой и наклонной. Решение задачи

Объем является характеристикой любой фигуры, имеющей ненулевые размеры во всех трех измерениях пространства. В данной статье с точки зрения стереометрии (геометрии пространственных фигур) мы рассмотрим призму и покажем, как находить объемы призм различного вида.

Что такое призма?

Стереометрия располагает точным ответом на этот вопрос. Под призмой в ней понимают фигуру, образованную двумя многоугольными одинаковыми гранями и несколькими параллелограммами. На рисунке ниже показаны четыре разные призмы.

Каждую из них можно получить следующим образом: необходимо взять многоугольник (треугольник, четырехугольник и так далее) и отрезок определенной длины. Затем каждую вершину многоугольника следует перенести с помощью параллельных отрезков в другую плоскость. В новой плоскости, которая будет параллельна исходной, получится новый многоугольник, аналогичный выбранному изначально.

Призмы могут иметь разный тип. Так, они могут быть прямыми, наклонными и правильными. Если боковое ребро призмы (отрезок, соединяющий вершины оснований) перпендикулярно основаниям фигуры, то последняя является прямой. Соответственно, если это условие не выполняется, то речь идет о наклонной призме. Правильная фигура - это прямая призма с равноугольным и равносторонним основанием.

Далее в статье мы покажем, как рассчитывать объем призмы каждого из названных типов.

Объем правильных призм

Начнем с самого простого случая. Приведем формулу объема призмы правильной, имеющей n-угольное основание. Формула объема V для любой фигуры рассматриваемого класса имеет следующий вид:

V = S_o*h.

То есть для определения объема достаточно рассчитать площадь одного из оснований S_o и умножить ее на высоту h фигуры.

В случае правильной призмы обозначим длину стороны ее основания буквой a, а высоту, которая равна длине бокового ребра, буквой h. Если основание n-угольник правильный представляет, то для расчета его площади проще всего воспользоваться следующей универсальной формулой:

S_n = n/4*a²*ctg(pi/n).

Подставляя в равенство значение числа сторон n и длину одной стороны a, можно вычислить площадь n-угольного основания. Отметим, что функция котангенса здесь вычисляется для угла pi/n, который выражен в радианах.

Учитывая записанное для S_n равенство, получаем конечную формулу объема призмы правильной:

V_n = n/4*a²*h*ctg(pi/n).

Для каждого конкретного случая можно записать соответствующие формулы для V, но все они однозначно следуют из записанного общего выражения. Например, для четырехугольной призмы правильной, которая в общем случае является прямоугольным параллелепипедом, получаем:

V₄ = 4/4*a²*h*ctg(pi/4) = a²*h.

Если в этом выражении принять h=a, то мы получаем формулу для объема куба.

Объем прямых призм

Отметим сразу, что для прямых фигур не существует общей формулы для вычисления объема, которая была приведена выше для правильных призм. При нахождении рассматриваемой величины следует использовать исходное выражение:

V = S_o*h.

Здесь h - это длина бокового ребра, как и в предыдущем случае. Что касается площади основания S_o, то она может принимать самые разные значения. Задача расчета у прямой призмы объема сводится к нахождению площади ее основания.

Расчет величины S_o следует проводить, исходя из особенностей самого основания. Например, если оно является треугольником, тогда площадь вычислить можно так:

S_o3 = 1/2*a*h_a.

Здесь h_a - апофема треугольника, то есть его высота, опущенная на основание a.

Если основанием является четырехугольник, то он может быть трапецией, параллелограммом, прямоугольником или иметь совершенно произвольный тип. Для всех названых случаев следует воспользоваться соответствующей формулой планиметрии для определения площади. Например, для трапеции эта формула имеет вид:

S_o4 = 1/2*(a₁ + a₂)*h_a.

Где h_a - высота трапеции, a₁ и a₂ - это длины ее параллельных сторон.

Чтобы определить площадь для многоугольников более высокого порядка, следует разбивать их на простые фигуры (треугольники, четырехугольники) и рассчитывать сумму площадей последних.

Объем наклонных призм

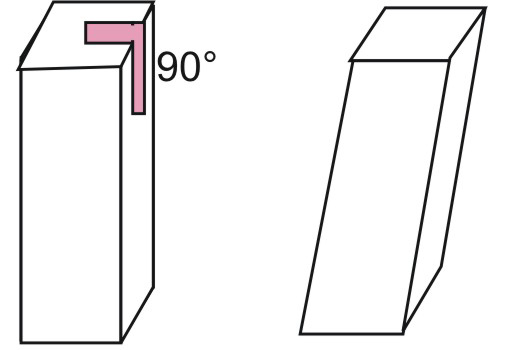
Это самый сложный случай расчета объема призмы. Общая формула для таких фигур также применима:

V = S_o*h.

Тем не менее, к сложности нахождения площади основания, представляющего многоугольник произвольного типа, добавляется проблема определения высоты фигуры. Она в наклонной призме всегда меньше длины бокового ребра.

Проще всего эту высоту найти, если известен какой-либо угол фигуры (плоский или двугранный). Если такой угол дан, тогда следует с его использованием построить внутри призмы прямоугольный треугольник, который бы содержал в качестве одной из сторон высоту h и, пользуясь тригонометрическими функциями и теоремой Пифагора, найти величину h.

Геометрическая задача на определение объема

Дана правильная призма с треугольным основанием, имеющая высоту 14 см и длину стороны 5 см. Чему равен объем треугольной призмы?

Поскольку речь идет о правильной фигуре, то мы вправе воспользоваться известной формулой. Имеем:

V₃ = 3/4*a²*h*ctg(pi/3) = 3/4*5²*14*1/√3 = √3/4*25*14 = 151,55 см³.

Треугольная призма является достаточно симметричной фигурой, в форме которой часто выполняют разные архитектурные сооружения. Эту призму из стекла используют в оптике.