Формула объема призмы. Объемы правильной четырехугольной и шестиугольной фигур

Призма является полиэдром или многогранником, который изучают в школьном курсе стереометрии. Одним из важных свойств этого многогранника является его объем. Рассмотрим в статье как можно вычислить эту величину, а также приведем формулы объема призм - правильных четырехугольной и шестиугольной.

Призма в стереометрии

Под этой фигурой понимают полиэдр, который состоит из двух одинаковых многоугольников, расположенных в параллельных плоскостях, и из нескольких параллелограммов. Для определенных видов призм параллелограммы могут представлять прямоугольные четырехугольники или квадраты. Ниже показан пример так называемой пятиугольной призмы.

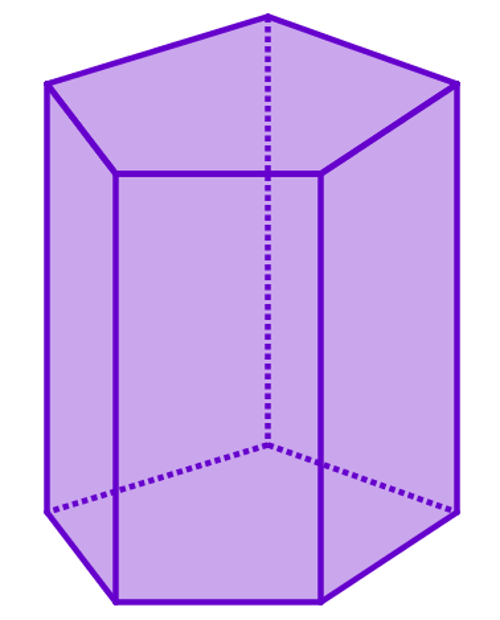
Чтобы построить фигуру как на рисунке выше, необходимо взять пятиугольник и выполнить его параллельный перенос на некоторое расстояние в пространстве. Соединив стороны двух пятиугольников с помощью параллелограммов мы получим искомую призму.

Всякая призма состоит из граней, вершин и ребер. Вершины призмы, в отличие от пирамиды, являются равноправными, каждая из них относится к одному из двух оснований. Грани и ребра бывают двух типов: те, что принадлежат основаниям, и те, что относятся к боковым сторонам.

Призмы бывают нескольких видов (правильные, наклонные, выпуклые, прямые, вогнутые). Рассмотрим далее в статье по какой формуле объем призмы рассчитывается, принимая во внимание вид фигуры.

Общее выражение для определения объема призмы

Независимо от того к какому виду относится изучаемая фигура, является ли она прямой или наклонной, правильной или неправильной, существует универсальное выражение, позволяющее определить ее объем. Объемом пространственной фигуры называют область пространства, которая заключена между ее гранями. Общая формула объема призмы выглядит так:

V = S_o × h.

Здесь S_o представляет собой площадь основания. Следует запомнить что речь идет именно об одном основании, а не о двух. Величина h - это высота. Под высотой изучаемой фигуры понимают расстояние между ее одинаковыми основаниями. Если это расстояние совпадает с длинами боковых ребер, тогда говорят о прямой призме. У прямой фигуры все боковые стороны являются прямоугольниками.

Таким образом, если призма является наклонной и имеет неправильный многоугольник в основании, то расчет ее объема усложняется. Если же фигура является прямой, то вычисление объема сводится только к определению площади основания S_o.

Определение объема правильной фигуры

Правильной называется любая призма, которая является прямой и имеет многоугольное основание с равными друг другу сторонами и углами. Например, такими правильными многоугольниками являются квадрат и равносторонний треугольник. В то же время ромб не является правильной фигурой, поскольку не все его углы равны между собой.

Формула объема призмы правильной однозначно следует из общего выражения для V, которое было записано в предыдущем пункте статьи. Прежде чем переходить к записи соответствующей формулы, необходимо определить площадь правильного основания. Не вдаваясь в математические подробности, приведем формулу определения указанной площади. Она носит универсальный характер для любого правильного n-угольника и имеет следующий вид:

S_n = n / 4 × ctg (pi / n) × a².

Как видно из выражения, площадь S_n - это функция двух параметров. Целое число n может принимать значения от 3 до бесконечности. Величина a - это длина стороны n-угольника.

Для вычисления объема фигуры необходимо лишь умножить площадь S_n на высоту h или на длину бокового ребра b (h=b). В итоге приходим к следующей рабочей формуле:

V = n / 4 × ctg (pi / n) × a² × h.

Заметим, что для определения объема призмы произвольного вида необходимо знать несколько величин (длины сторон основания, высоту, двугранные углы фигуры), для расчета же величины V правильной призмы нам следует знать лишь два линейных параметра, например, a и h.

Объем призмы четырехугольной правильной

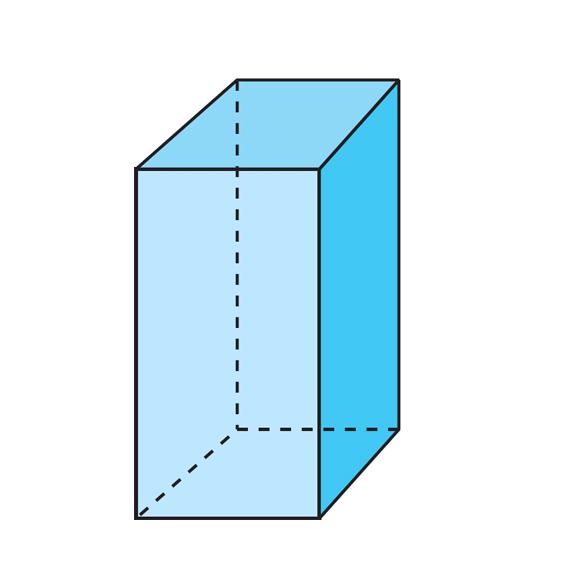
Четырехугольная призма называется параллелепипедом. Если у нее все грани равны и представляют собой квадраты, то такая фигура будет кубом. Каждый школьник знает, что объем прямоугольного параллелепипеда или куба определяется в результате умножения трех его различных сторон (длины высоты и ширины). Этот факт следует из записанного общего выражения объема для правильной фигуры:

V = n/4 × ctg (pi / n) × a² × h = 4/4 × ctg ( pi / 4) × a² × h = a² × h.

Здесь котангенс от 45° равен 1. Заметим, что равенство высоты h и длины стороны основания a автоматически приводит к формуле объема куба.

Объем призмы шестиугольной правильной

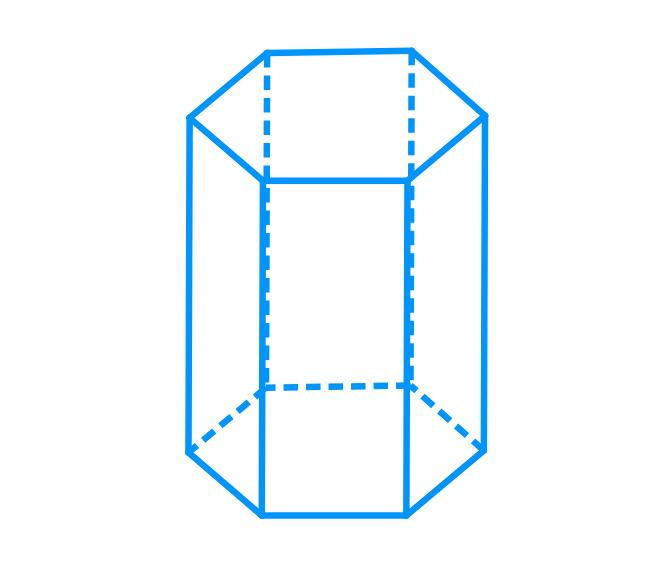
Теперь применим изложенную выше теорию для определения объема фигуры с шестиугольным основанием. Для этого следует лишь подставить значение n=6 в формулу:

V = 6/4 × ctg (pi / 6) × a² × h = 3 × √3/2 × a² × h.

Записанное выражение можно получить самостоятельно, не пользуясь универсальной формулой для S_n. Чтобы это сделать необходимо разделить правильный шестиугольник на шесть равносторонних треугольников. Сторона каждого из них будет равна a. Площадь одного треугольника соответствует:

S₃ = √3/4 × a².

Умножив эту величину на количество треугольников (6) и на высоту, мы получим записанную выше формулу для объема.