Для экономистов часто необходимо оптимизировать производственную функцию, максимизировать или минимизировать ее, например, прибыль, убыток или другие данные с учетом линейного ограничения. Понимание задач линейного программирования и постановка задач — это требует знания основ математики и статистики. Задачей линейного программирования (LP) является определение функции для получения оптимальных данных. Это один из самых важных инструментов исследования бизнес-операций. Он также широко используется в качестве помощи при принятии решений во многих отраслях: в областях экономики, компьютерных наук, математики и других современных практических исследованиях.
Характеристики задач линейного программирования
Различают следующие характеристики LP:
- Оптимизация. Основой задач линейного программирования и постановки задач оптимизации является максимизация либо минимизация некоторой базы данных, являющейся предметом исследования. Такое часто встречается в экономике, бизнесе, рекламе и многих других областях, которые требуют эффективности с целью сохранения ресурсов. Сюда относятся вопросы получения прибыли, приобретения ресурсов, время производства и другие важные экономические показатели.
- Линейность. Как следует из названия, все задачи LP имеют признак линейности. Однако он порой вводит в заблуждение, так как линейность относится только к переменным 1 степени, исключая степенные функции, квадратные корни и другие нелинейные зависимости. При этом она не означает, что функции задачи LP имеют только одну переменную. Она относится к переменным как к координатам точек на прямой, исключая любую кривизну.
- Объективная функция. Основа задач линейного программирования и постановки задач объективности — переменные, изменяемые по желанию, например, время, потраченное на работу, произведенные единицы товара. Целевая функция пишется с заглавной буквы «Z».
- Ограничения. Все LP ограничиваются переменными внутри функции. Эти ограничения принимают форму неравенств, например, «b<3», где b может представлять единицы книг, написанных автором в месяц. Эти неравенства устанавливают, как можно максимизировать/минимизировать целевую функцию, поскольку вместе они определяют области принятия решения.
Условия определение задач

Компании стремятся получить наибольшую доходность в своей деятельности, поэтому должны максимально использовать имеющиеся у них ресурсы: человеческий, материалы, оборудование, средства и другие. LP представляется как полезный инструмент, помогающий определению лучшего решения в компании.
Условия выполнения задач линейного программирования и постановки задач необходимы для получения максимальной чистой прибыли. Для того чтобы решить задачу LP, она должна иметь:
- Ограничения или ограниченные ресурсы, например, ограниченное количество работников, максимальное количество клиентов или ограничение производственных потерь.
- Цель: максимизация дохода или минимизация затрат.
- Пропорциональную линейность. Уравнения, которые генерируют решающие переменные, должны быть линейными.
- Однородность: характеристики переменных решения и ресурсов одинаковы. Например, часы работы человека одинаково продуктивны или товары, изготовленные на станке, идентичны.
- Делимость: продукты и ресурсы могут быть показаны в виде дроби.
- Отсутствие отрицательности: решения должны быть положительными или равными нулю.
Объективность функции при постановке основной задачи линейного программирования математически выражает цель, которая должна быть достигнута в решении проблемы. Например, максимизировать прибыль компании или минимизировать производственные затраты.
Это представляется уравнением с переменным решением, где: X 1, X 2, X 3, ..., X n — переменные решения; C 1, C 2, C 3, ..., C n — константы.
Каждое ограничение выражается математически с любым из этих признаков:
- Меньше или равно (≤). Когда есть верхний предел, например, сверхурочная работа не может быть более 2 часов в день.
- Равен (=). Указывает обязательные отношения, например, конечный запас равен начальному запасу плюс производство минус продажи.
- Больше или равно (≥). Например, когда существует нижний предел, производство определенного продукта должно быть выше, чем прогнозируемый спрос.
- Общая постановка задачи линейного программирования начинается с установки ограничений.
- Любая задача LP должна иметь одно или несколько ограничений.
- Положительность переменных решения должна рассматриваться в рамках ограничений.
Этапы постановки задач
Общая постановка задачи линейного программирования и ее формулировка относится к переводу реальной проблемы к виду математических уравнений, которые могут быть решены.

Шаги постановки задачи целочисленного линейного программирования:
- Определяют число, выявляющее поведение целевой функции для оптимизации.
- Находят набор ограничений и выражают их в виде линейных уравнений или неравенств. Это установит область в n-мерном пространстве оптимизированных функций.
- Необходимо наложить условие неотрицательности на переменные задачи, то есть все они должны быть положительными.
- Выражают функцию в форме линейного уравнения.
- Оптимизируют функцию графически или математически, когда выполняется математическая постановка задачи линейного программирования.
Графический способ
Графический метод используется для выполнения задач LP в двух переменных. Этот метод не применяется для решения проблем, которые имеют три или более переменных решений.
Стандартная задача максимизации неизвестных проблем LP, в которой увеличивают функцию, при условии ограничений вида:
x ≥ 0, y ≥ 0, z ≥ 0 и дальнейшие ограничения формы:
Ax + By + C z +. , ≤ N,
где А, В, С и N являются неотрицательными числами.
Неравенство должно быть «≤», а не «=» или «≥».
Графический метод LP с двумя неизвестными состоит в следующем:
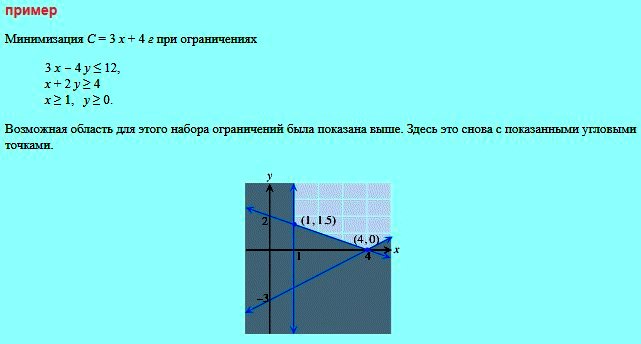
- Устанавливают возможные области графика.
- Вычисляют угловые координаты точек.
- Подставляют их с целью увидеть оптимальное значение. Этот момент дает решение задачи LP.
- Минимизируют функцию и, если ее коэффициенты неотрицательны, решение существует.
Определение существующих решений:
- Ограничивают область, добавив вертикальную линию справа от крайней правой угловой точки и горизонтальную линию выше самой высокой угловой точки.
- Рассчитывают координаты новых угловых точек.
- Находят угловую точку с оптимальным значением.
- Если оно имеет место в исходной точке неограниченной области, то у задачи LP есть решение в данной точке. Если нет, то она не имеет оптимального решения.
Зарисовка набора решений
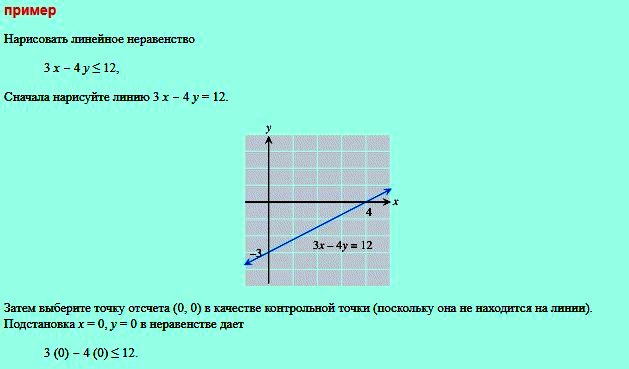
Выбирают точку отсчета и отмечают блокируемую область.
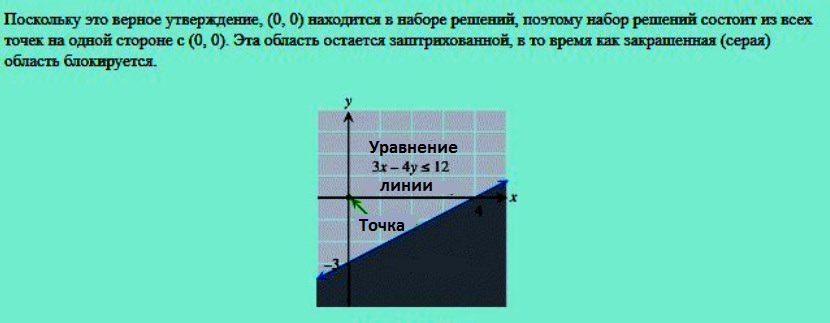
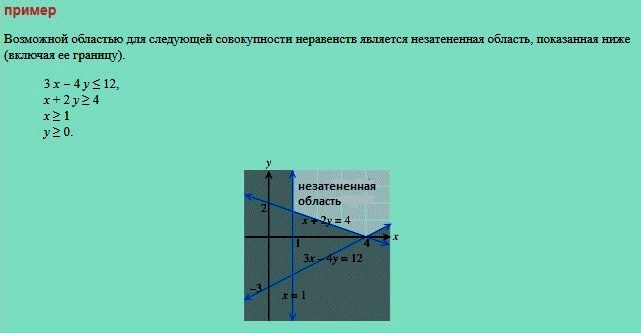
Рисуют область, представленную неравенством двух переменных при постановке задачи линейного программирования. Кратко для примера:
- Рисуют прямую, полученную путем замены неравенства на равенство.
- Выбирают контрольную точку, (0,0). Хороший выбор, если линия проходит через начало.
- Если контрольная точка удовлетворяет неравенству, то множество решений — это вся область на той же стороне линии, что и контрольная точка. В противном случае она находится на другой стороне линии.
- Допустимая область определяется набором линейных неравенств и является совокупностью точек, удовлетворяющих все неравенства.
- Чтобы нарисовать ее, определяемую набором линейных неравенств с двумя переменными, выполняют области, представленные каждым неравенством, на одном графике, не забывая затенять части плоскости, которые не нужны.
Симплексный метод для максимизации
Постановку задачи линейного программирования с математической моделью для максимизации можно выполнить с применением симплекс-метода:
- Преобразуют данные в систему уравнений, вводя слабые переменные, чтобы превратить ограничения в уравнения, и переписывают функцию в стандартную форму.
- Записывают исходную таблицу.
- Выбирают столбец разворота, отрицательное число с наибольшей величиной в нижнем ряду, исключая крайнюю правую запись. Его столбец является сводным. Если есть два кандидата, выбирают один. Если все числа в нижнем ряду равны нулю или положительны, исключая крайнюю правую запись, то все готово и базовое решение максимизирует целевую функцию.
- Выбирают стержень в столбце. Ось всегда должна быть положительным числом. Для каждой положительной записи «b» в столбце сводных данных вычисляют отношение «a/b», где "a" является ответом в этой строке. Из тестовых коэффициентов выбирают минимальное, тогда соответствующее число «b» будет являться осью.
- Используют стержень, чтобы очистить столбец обычным способом, следя за тем, чтобы точно выполнять предписания для формулировки операций со строками, описанным в руководстве по методу Гаусса-Джордана, а затем меняют местами столбец с меткой из колонки.
- Переменная, изначально обозначающая строку сводки, является выходящей, а переменная, обозначающая столбец, является входящей.
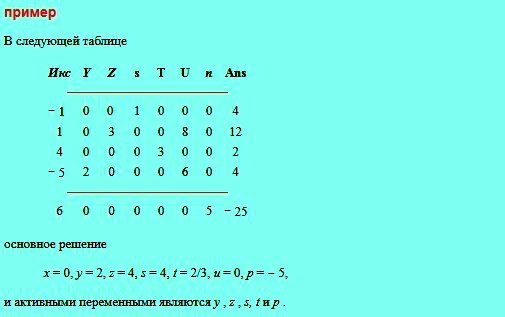
Для того чтобы получить базовое решение, соответствующее любой таблице в симплекс-методе, устанавливают в ноль все переменные, которые не отображаются, как метки строк. Значение отображаемой метки строки (активная переменная) — число в крайнем правом столбце в строке, разделенное на число в этой строке в столбце, помеченном той же переменной.
Нестандартные ограничения
Для того чтобы решить задачу LP с ограничениями вида (Ax + By +. , .≥ N) с положительным N, вычитают лишнюю переменную из левой части (вместо добавления слабой переменной). Базовое решение, соответствующее исходной таблице, не будет выполнимо, поскольку некоторые из активных переменных будут отрицательными. Поэтому правила начального поворота отличаются от приведенных выше.
Далее помечают все строки, которые дают отрицательное значение для связанной активной переменной, за исключением целевой. Если есть помеченные строки, нужно начать с I этапа.
I этап. В первой строке находят наибольшее положительное число. Используют тестовые коэффициенты, как в предыдущем разделе, чтобы найти сводку в этом столбце, а затем разворачивают эту запись. Повторяют до тех пор, пока не останется помеченных строк, затем переходят к этапу II.
II этап использует симплекс-метод для стандартной задачи максимизации. Если в левом нижнем ряда после I этапа есть какие-либо отрицательные значения, используют метод стандартных задач максимизации.

Пример игры, которая может быть решена с использованием симплекс-метода.
Онлайн инструмент PHPSimplex
В настоящее время технологические инструменты облегчают многие виды деятельности профессиональной жизни и методы решения задач LP не являются исключением. Преимущество их состоит в том, что можно получить оптимальное решение с любого компьютера с доступом в интернете.
PHPSimplex — отличный онлайн-инструмент для решения задач LP. Это приложение может решать проблемы без ограничений по количеству переменных и ограничений. Для задач с двумя переменными он демонстрирует графическое решение и представляет весь процесс вычисления оптимального решения простым и понятным способом. Он имеет дружественный интерфейс, близок к пользователю, прост в использовании и интуитивно понятен, доступен на нескольких языках.
WanerMath: приложения без границ
Warneth предоставляет 2 инструмента для решения задач линейного программирования:
- График линейного программирования (две переменные).
- Симплексный метод.
В отличие от других инструментов, где размещают только коэффициенты, здесь включаются все функции с переменными. Это не представляет большой трудности для начинающих пользователей, так как на профильном сайте есть инструкция по использованию. В дополнение, на сайте есть функция «Примеры», которая автоматически создает задачи, чтобы пользователь мог оценить его работу, например, при постановке транспортной задачи линейного программирования.
JSimplex — еще один инструмент онлайн. Он позволяет решать задачи LP без ограничения количества переменных. Имеет простой интерфейс управления, в котором предлагается указать цель и количество переменных. Пользователь записывает коэффициенты целевой функции, ограничения и нажимает на «решить». Будет показана интеграция, расчет оптимального варианта и результаты каждой переменной.
Как видно, эти инструменты чрезвычайно полезны для легкого изучения процедур решения линейного программирования.
Простой пример LP
Компания выпускает портативные и калькуляторы для научных работ. Долгосрочные прогнозы указывают на ожидаемую ежедневную потребность в 150 научных и 100 портативных калькуляторах. Суточная производственная мощность ежедневно позволяет производить не более 250 научных и 200 портативных калькуляторов.
Для того чтобы выполнить контракт на доставку, необходимо выпустить минимум 250 калькуляторов. Реализация одного — приводит к убытку 20 рублей, но каждый ручной калькулятор приносит прибыль в размере 50 рублей. Необходимо выполнить расчет, чтобы получить максимальную чистую прибыль.
Алгоритм выполнения примера постановки задач линейного программирования:
- Переменные решения. Поскольку было задано оптимальное количество калькуляторов, именно они будут переменными я в этой задаче: x — количество научных калькуляторов, y — количество портативных.
- Устанавливают ограничения, поскольку компания не может произвести отрицательное количество калькуляторов в день, естественным ограничением будет: x ≥ 0, y ≥ 0.
- Нижняя граница: x ≥ 150, y ≥ 100.
- Устанавливают верхнюю границу для этих переменных из-за ограничений на производство компанией: x ≤ 250, y ≤ 200.
- Совместное ограничение на значения 'x' и 'y' из-за минимального заказа на отправку груза: х + у ≥ 250
- Оптимизируют функцию чистой прибыли: P = -20x + 50y.
- Решение задачи: максимизация P = -20x + 50y при условии, что 150 ≤ x ≤ 250; 100 ≤ y ≤ 200; x + y ≥ 250.
Области применения
Среди применений линейного программирования наиболее распространены:
- Совокупное планирование продаж и операций. Цель состоит в том, чтобы минимизировать производственные затраты в краткосрочной перспективе, например, три и шесть месяцев, удовлетворяющих ожидаемый спрос.
- Планирование продукта: находят оптимальное сочетание продуктов, учитывая, что они требуют разных ресурсов и имеют разные затраты. В качестве примера можно найти оптимальную смесь химических элементов для бензина, красок, диет для человека и кормов для животных.
- Производственный поток: определяют оптимальный поток для производства продукта, который должен проходить последовательно через несколько рабочих процессов, где каждый имеет свои затраты и производственные характеристики.
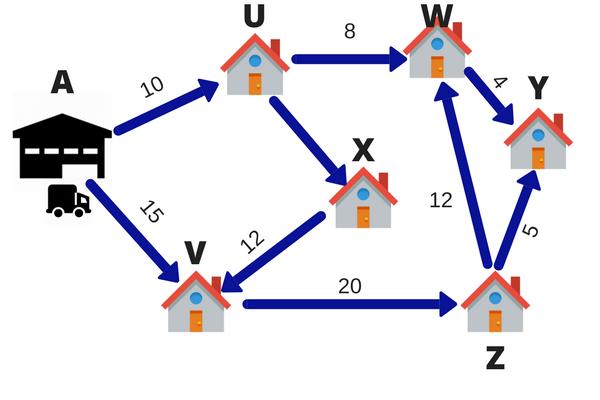
- Постановка транспортной задачи линейного программирования, расписание перевозок. Метод используется для программирования нескольких маршрутов определенного количества транспортных средств для обслуживания клиентов или получения материалов, которые будут перевозиться между различными местами. Каждое транспортное средство может иметь различную грузоподъемность и производительность.
- Управление запасами: определение оптимальной комбинации продуктов, которые будут в наличии на складе в продажной сети.
- Программирование персонала: разработка плана по кадрам, который позволяет удовлетворить ожидаемый переменный спрос на специалистов при минимально возможном количестве сотрудников.
- Контроль отходов: с помощью линейного программирования можно рассчитать, как сократить отходы до минимума.
Это некоторые из наиболее распространенных применений, где используется линейное программирование. В общем, любая задача оптимизации, которая удовлетворяет вышеуказанным условиям, может быть решена с его помощью.


























