Диагональ прямоугольника: свойства и формулы

Диагональ прямоугольника - важный элемент этой геометрической фигуры. Знание свойств диагоналей помогает решать множество задач и доказывать утверждения. В статье мы подробно разберем, что такое диагональ прямоугольника, рассмотрим ее свойства и основные формулы для вычисления.

Что такое диагональ прямоугольника

Диагональ прямоугольника - это отрезок, соединяющий две противоположные вершины прямоугольника. Обозначается обычно буквой d или двумя заглавными буквами по названию соединяемых вершин, например AC.

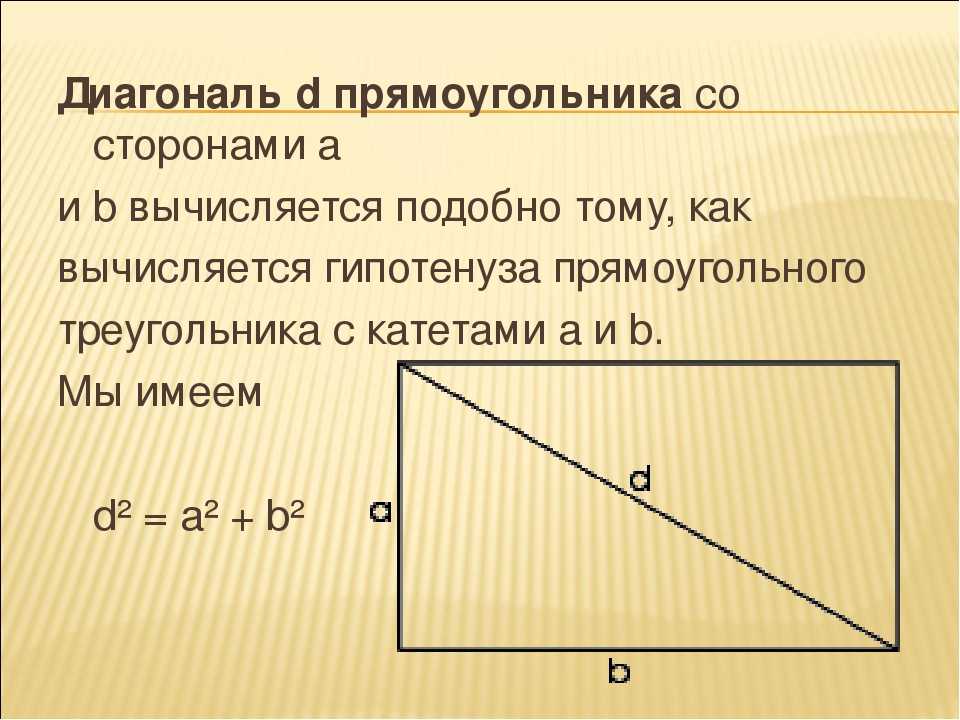
Как видно на рисунке, диагональ делит прямоугольник на два прямоугольных треугольника. Это важное свойство диагонали, которое используется при решении многих задач.

Формула для вычисления диагонали прямоугольника

Длину диагонали прямоугольника можно найти по следующей формуле:

d = √(a2 + b2)

где a и b - длины сторон прямоугольника.

Эта формула получается из теоремы Пифагора, примененной к прямоугольному треугольнику, на который диагональ делит прямоугольник.

Основные свойства диагонали прямоугольника

Рассмотрим свойства диагонали прямоугольника:

1. Диагонали пересекаются в одной точке.
2. Точка пересечения диагоналей делит их пополам.
3. Диагонали прямоугольника равны между собой.

Последнее свойство особенно важно и часто используется на практике. Оно позволяет по длине одной диагонали находить другую. Это свойство также используется как признак прямоугольника: если диагонали параллелограмма равны, значит это прямоугольник.

Применение свойств диагоналей прямоугольника

Свойства диагоналей прямоугольника широко используются на практике:

• При нахождении площади прямоугольника
• При вычислении периметра прямоугольника через диагональ и стороны треугольников, на которые диагональ делит прямоугольник.
• При доказательстве того, что некоторый параллелограмм является прямоугольником.

Рассмотрим пример задачи на применение свойств диагоналей прямоугольника:

Докажите, что параллелограмм ABCD с диагоналями AC = 5 см и BD = 5 см является прямоугольником.

Решение: Из условия задачи известно, что в параллелограмме ABCD диагонали равны между собой и равны 5 см. Согласно свойству диагоналей прямоугольника, если диагонали параллелограмма равны, значит этот параллелограмм является прямоугольником.

Значит, параллелограмм ABCD является прямоугольником.

В этой задаче мы использовали свойство равенства диагоналей прямоугольника для доказательства того, что данный параллелограмм является прямоугольником.

Выводы

Итак, мы рассмотрели основные свойства диагоналей прямоугольника и формулы для их вычисления. Убедились на конкретном примере задачи, как эти свойства помогают в решении геометрических задач и доказательстве утверждений.

Владение свойствами диагоналей прямоугольника важно для изучения геометрии. Эти свойства позволяют решать задачи, в которых нужно найти площадь или периметр прямоугольника, а также используются как признаки прямоугольника среди других четырехугольников.

Другие применения свойств диагоналей

Кроме уже упомянутых случаев, свойства диагоналей прямоугольника можно использовать:

• При решении задач на доказательство равенства треугольников. Например, если известно, что в четырехугольнике диагонали равны, то треугольники, на которые эти диагонали делят четырехугольник, также равны.
• В задачах на построение, когда нужно построить прямоугольник по заданным параметрам. Зная свойство равенства диагоналей, можно корректно построить искомый прямоугольник.
• При выводе формул для вычисления элементов прямоугольника через другие его элементы. Например, формулы радиусов вписанной и описанной окружностей.
  

Занимательные факты о диагоналях

Рассмотрим несколько интересных фактов, связанных с диагоналями прямоугольника:

1. Диагональ квадрата, являющегося частным случаем прямоугольника, выражается иррациональным числом. Поэтому древние греки называли ее «несоизмеримой величиной».
2. Существует мнемоническое правило для запоминания того, что диагонали прямоугольника равны: «Две дамы диагонали никогда не ссорятся».
3. Интересный парадокс: периметр прямоугольника всегда больше суммы его диагоналей. Но если стороны прямоугольника стремятся к бесконечности, то периметр и сумма диагоналей становятся равными.

Эти и другие интересные факты о диагоналях прямоугольника показывают, насколько важной является эта тема в геометрии.

Вычисление параметров прямоугольника через диагонали

Помимо уже рассмотренных случаев, знание диагоналей прямоугольника позволяет вычислить такие его параметры, как:

• Стороны (из теоремы Пифагора)
• Периметр
• Площадь (через теорему синусов)
• Радиусы вписанной и описанной окружности