Координатная плоскость - фундаментальное понятие математики, лежащее в основе современных технологий навигации, компьютерной графики, физических вычислений и многого другого. Но что же она представляет собой на самом деле и как ей пользоваться?
Определение координатной плоскости
Координатная плоскость - это плоскость, на которой введена система координат для задания положения точек. Она состоит из двух пересекающихся под прямым углом числовых осей - горизонтальной оси абсцисс X и вертикальной оси ординат Y. Их пересечение называется началом координат, а сами оси делят плоскость на 4 четверти.
Любая точка на такой плоскости однозначно задается упорядоченной парой чисел - ее координатами (x; y). Первое число показывает положение точки на оси X, второе - на оси Y. Например, точка A с координатами (3; 2) находится на расстоянии 3 единицы от начала координат по горизонтали и 2 единицы по вертикали.
Координатную плоскость можно увидеть в действии в таких знакомых вещах как шахматная доска или игра "Морской бой", где каждая клетка или часть поля также имеет свои "координаты".
Итак, координатная плоскость - это удобный математический инструмент, позволяющий задавать положение точек и строить различные геометрические фигуры, графики функций и многое другое. Давайте теперь разберемся, как ее правильно построить.
Как правильно строить координатную плоскость
Для построения координатной плоскости нам понадобятся всего лишь линейка, карандаш и лист бумаги. Вот пошаговая инструкция:
- Проводим горизонтальную прямую посередине листа. Это будет наша ось X (абсцисс).
- Отмечаем на ней point и подписываем под прямой X. Это начало координат.
- Справа и слева от точки 0 наносим единичные отрезки (например, 1 см), пронумеровываем их.
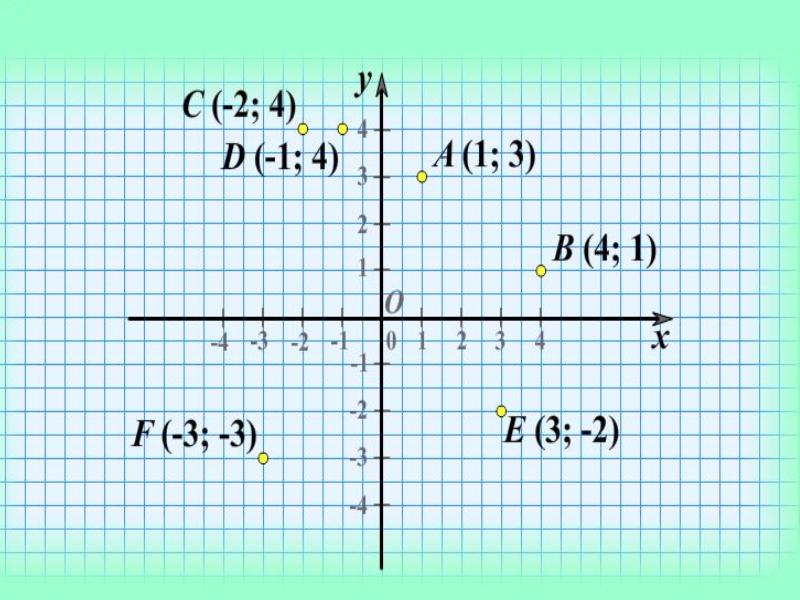
Аналогично проводим вторую прямую - ось Y, обозначаем ее пересечение с осью X точкой 0, наносим ординаты. Получаем классическую декартову систему координат.
Теперь наша плоскость готова к работе! Мы можем задавать на ней точки, чертить различные фигуры, графики и многое другое. Рассмотрим это подробнее в следующем разделе.
Нанесение точек и фигур на координатную плоскость
Итак, у нас есть координатная плоскость с двумя осями X и Y. Давайте попрактикуемся в нанесении на нее точек по заданным координатам. Например, имеем point с координатами (2; 3). Алгоритм следующий:
- На оси X отмечаем число 2.
- На оси Y отмечаем число 3.
- Из полученных точек проводим перпендикуляры к осям.
- Точка их пересечения и есть искомая точка с заданными координатами.
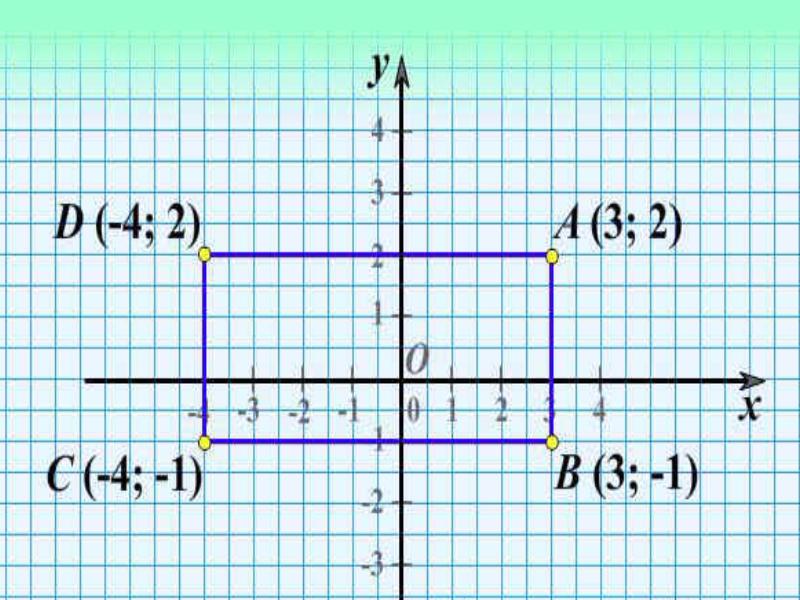
Попробуйте нанести несколько точек самостоятельно! А теперь давайте нарисуем прямоугольник. Для этого нам понадобятся координаты его вершин. Предположим, у нас есть 4 точки:
| A (1; 2) | B (4; 2) |
| C (4; 5) | D (1; 5) |
Наносим эти точки на плоскость, соединяем отрезками - и получаем нужный прямоугольник со сторонами 3 и 3. Так же можно строить треугольники, окружности, любые другие фигуры.
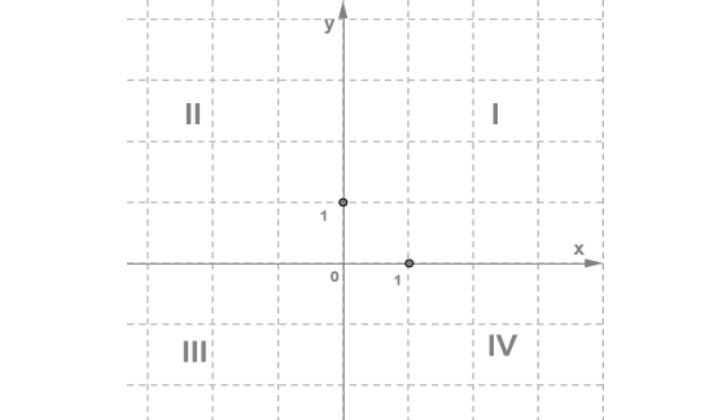
Координатные четверти
Любую координатную плоскость можно разделить на 4 четверти в зависимости от знаков координат точек:
- I четверть - X и Y положительные
- II четверть - X отрицательная, Y положительная
- III четверть - X и Y отрицательные
- IV четверть - X положительная, Y отрицательная
Это важно знать при работе с координатной плоскостью. Например, по знакам координат точки можно сразу определить, в какой четверти она находится.
Отображение прямых линий
Координатная плоскость также удобна для отображения прямых в виде линейных уравнений. Например, вертикальная прямая X = 3 проходит параллельно оси Y через все точки с абсциссой, равной 3. А горизонтальная прямая Y = -2 идет параллельно оси X на уровне ординаты -2.
Зная уравнение прямой, мы можем легко построить ее график на координатной плоскости. А если задан график - записать уравнение.
Что такое координатная плоскость: определение
Итак, еще раз определим: координатная плоскость - это плоскость, на которой задана система координат, состоящая из двух перпендикулярных осей OX и OY. С помощью этих осей можно однозначно задать положение любой точки упорядоченной парой чисел (X; Y) - ее координатами.
Задачи на координатной плоскости
Работа с координатной плоскостью - важная часть школьного курса математики. Рассмотрим несколько типовых задач, с которыми приходится сталкиваться.
Например, даны координаты точек A(2; 3) и B(5; -2). Требуется найти длину отрезка AB и его середину. Построим этот отрезок на координатной плоскости, используя известные нам координаты концов. Длина отрезка вычисляется по формуле:
Подставляем значения, получаем ответ: 5. Аналогично находим координаты середины:
Графики функций
Еще одно важное применение координатной плоскости - построение графиков функций. Задав зависимость между переменными X и Y в виде формулы, мы можем найти соответствующие значения Y при конкретных X. Нанося эти точки на плоскость, получаем график функции.
Например, пусть задана функция Y = 2X + 1. При X = -2 значение Y равно -3. Это точка (-2; -3) на нашем графике. Аналогично находим другие точки и соединяем их плавной линией. В итоге получаем график прямой линии с угловым коэффициентом 2.



























