Положительные и отрицательные числа - неотъемлемая часть математики, с которыми мы сталкиваемся повсеместно. Давайте разберемся, что они из себя представляют, в чем их плюсы и минусы, и почему важно понимать их особенности.
Основные понятия и определения
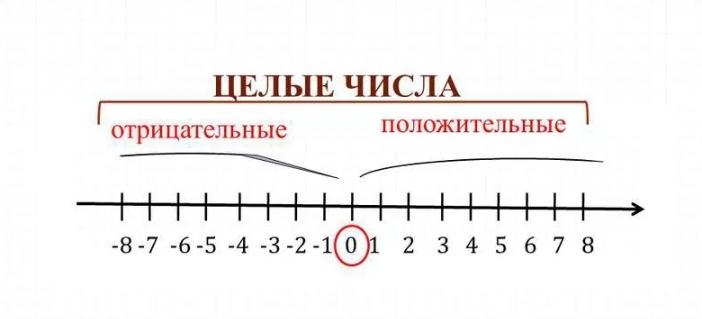
Чтобы разобраться с положительными и отрицательными числами, давайте начнем с азов и вспомним, что же это такое. По определению, положительные числа– это числа со знаком «+» перед ними (знак «+» обычно не пишут), отрицательные числа– это числа, перед которыми стоит знак «–». Нуль не относится ни к положительным, ни к отрицательным числам. Он их разделяет.Отрицательные числа используют для обозначения различных величин, таких как температура (ниже нуля), расход – то есть отрицательный доход, глубина –отрицательная высота и другие.
Положительные числа
Положительными называются числа, которые больше нуля. Они не имеют знака "минус" перед собой. Примеры положительных чисел:
- 1, 2, 3, 4, 5...
- 0,25
- 2,71828 (число э)
- 3,14159 (число π)
Любые натуральные числа, дроби, десятичные дроби, корни, степени с основанием больше 0 являются положительными.
Отрицательные числа
Отрицательные числа - это числа, меньшие нуля, перед которыми стоит знак "минус". Примеры отрицательных чисел:
- -1, -2, -3, -4, -5...
- -0,25
- -2,71828
- -3,14159
Любое число с знаком минус перед собой считается отрицательным.
Нулевое число
Особняком стоит ноль - он не является ни положительным, ни отрицательным числом. Ноль находится как бы посередине между положительными и отрицательными числами.
Правила сложения и вычитания

Теперь давайте разберем, как складывать и вычитать положительные и отрицательные числа. Здесь есть несколько важных правил, которые нужно знать.
Основные правила сложения положительных и отрицательных чисел
При сложении чисел со знаками действует несколько простых правил:
- Плюс и плюс дает плюс:
+2 + +3 = +5 - Минус и минус дает минус:
-2 + -3 = -5 - Плюс и минус дает разность модулей этих чисел:
+5 + -3 = +2
То есть при сложении положительного и отрицательного числа мы находим разность модулей и ставим знак большего по модулю числа. Не стоит
- целые положительные и отрицательные числа
Целые положительные и отрицательные числа — это те же самые числа, только они являются целыми, то есть не дробными и не десятичными. Примеры:
- Положительные: 1, 2, 3, 547, 1024
- Отрицательные: -1, -2, -3, -365, -100000
При сложении целых положительных и отрицательных чисел действуют те же правила, что и для всех остальных.
| +5 + 2 = 7 | +(-10) + (-7) = -17 |
| +3 + (-4) = -1 | +(-100) + 7 = - 93 |
Как видно из примеров, ничего не меняется — просто числа являются целыми вместо дробных или десятичных.
Основные правила вычитания положительных и отрицательных чисел
Аналогичные простые правила действуют и при вычитании:
- Плюс минус минус дает плюс:
+5 - -3 = +8 - Минус минус минус дает минус:
-7 - -4 = -3 - Плюс минус плюс дает минус:
+6 - +1 = +5
При вычитании положительного из положительного мы просто находим разность.
Использование в физике и технике: измерительные приборы
Одно из самых распространенных применений — это измерительные приборы, такие как термометры или манометры. На них часто используется шкала со значениями выше и ниже нуля:
- На термометре температуры выше 0 градусов отмечаются положительными числами, а ниже — отрицательными.
- На манометре давление выше атмосферного обозначается положительными значениями, а разрежение (давление ниже атмосферного) — отрицательными.
Таким образом, положительные и отрицательные числа позволяют наглядно отображать отклонение измеряемой величины от некоторого условного "нуля".
Применение в экономике и финансах: доходы, расходы, прибыль, убытки
Еще одно популярное применение — использование в экономике и финансах для обозначения доходов и расходов:
- Положительные числа - это доходы и прибыль.
- Отрицательные числа - расходы и убытки.
Например, если компания в прошлом году получила прибыль в размере 500 млн рублей, это записывается как +500 млн. А если компания понесла убыток 250 млн рублей, то это будет -250 млн.
Такое представление позволяет наглядно видеть финансовые потоки и оперировать ими при расчетах.
Использование в географии и навигации: положение объектов на карте
В географии положительные и отрицательные числа часто используются для обозначения координат:
- Положительные значения широты - к северу от экватора.
- Отрицательные значения широты - к югу от экватора.
Аналогично для долготы:
- Положительные значения - к востоку от нулевого меридиана.
- Отрицательные значения - к западу от него.
Это позволяет точно определять положение любых объектов на земной поверхности.























