Деление дробей - одна из важных и в то же время сложных тем школьного курса математики. Многие ученики сталкиваются с трудностями при изучении этой темы. В этой статье мы подробно разберем основные правила и рассмотрим примеры деления обыкновенных дробей на обыкновенные дроби и целые числа.
Основные понятия и определения
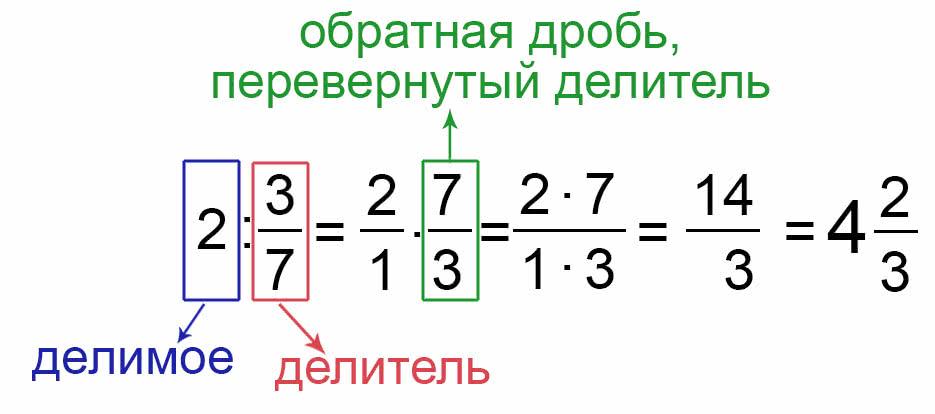
Прежде чем переходить непосредственно к изучению правил и примеров деления, давайте разберемся в основных терминах.
Дробь - это числовое выражение, состоящее из двух частей: числителя и знаменателя, разделенных чертой.
- Числитель - верхняя часть дроби;
- Знаменатель - нижняя часть дроби.
Различают несколько видов дробей:
- Правильные - у которых числитель меньше знаменателя;
- Неправильные - у которых числитель больше или равен знаменателю;
- Смешанные - состоят из целой и дробной части.
Деление дробей - это арифметическое действие, при котором одну дробь делят на другую. Первая дробь называется делимым, вторая - делителем. Результат деления называют частным.
| Делимое | Дробь, которую делят |
| Делитель | Дробь, на которую делят |
| Частное | Результат деления (новая дробь) |
Правила деления обыкновенной дроби на обыкновенную дробь
Чтобы разделить одну обыкновенную дробь на другую, нужно выполнить 3 основных шага:
- Заменить деление умножением
- Найти дробь, обратную делителю
- Перемножить обе дроби
Рассмотрим эти шаги подробнее на конкретном числовом примере.
Допустим, нам нужно разделить дробь 2/3 на дробь 5/4
- Заменяем деление умножением. Вместо того, чтобы делить одну дробь на другую, будем умножать первую дробь на дробь, обратную второй:
- Находим обратную дробь к делителю 5/4. Для этого меняем числитель и знаменатель местами. Получаем 4/5:
- Перемножаем дроби: 2/3 и 4/5. Перемножаем числители: 2×4=8. Перемножаем знаменатели: 3×5=15. Итого: 2/3 ÷ 5/4 = 2/3 × 4/5 = 8/15
Итак, чтобы разделить дробь 2/3 на дробь 5/4, мы должны:
- Заменить деление на умножение
- Найти дробь, обратную делителю 5/4. Это будет дробь 4/5
- Перемножить делимое 2/3 и обратную дробь 4/5
В результате получаем частное 8/15.
Таким образом, общая формула деления обыкновенных дробей выглядит так:
a/b ÷ c/d = a/b × d/c
где a/b - делимое, c/d - делитель.
Другими словами, чтобы разделить одну дробь на другую, нужно:
- Поменять числитель и знаменатель местами у делителя - получится его обратная дробь
- Перемножить делимое и обратную дробь по правилам умножения
"Частным двух дробей называют дробь, которая при умножении на делитель дает делимое"
Правило деление дроби на целое число
Теперь, когда мы разобрали основные правила деления между дробей, то можем приступить к основной теме. Деление на целое число не сильно отличается от прошлых примеров, единственное нужно перевести целое число в дробь. К примеру 5 = 5/1. А дальше все происходит так же как при деление дробей.

Типичные ошибки при делении дробей на целые числа
Несмотря на кажущуюся простоту, деление дробей часто вызывает ошибки из-за невнимательности или непонимания правил. Давайте разберем типичные ошибки, которые допускают ученики 6 класса при делении дробей на целые числа.
Неправильное применение формулы
Одной из распространенных ошибок является неверное применение формулы деления дроби на число. Вместо того, чтобы умножать знаменатель на число, ученики начинают умножать на него числитель. Это приводит к неправильному ответу.
Ошибки при сокращении дробей
Еще одна типичная для 6 класса ошибка - неумение правильно сокращать дроби. Получив ответ в виде неправильной дроби, многие ученики забывают ее сократить и упростить.
Неверная проверка результата
После выполнения деления дробей на целое число важно проверить правильность результата. Однако учащиеся часто не догадываются это сделать или допускают ошибки при проверке.
Рекомендации по предотвращению ошибок
Чтобы избежать типичных ошибок при делении дробей на целые числа, рекомендуем:
- Хорошо выучить формулы и последовательность действий
- Составить шпаргалку с примерами
- Обязательно проверять результат
Закрепление материала

Итак, мы подробно разобрали процесс деления обыкновенных дробей на обыкновенные дроби и на целые числа. Рассмотрели конкретные числовые примеры.

























