Магнитные поля играют важную роль в современной науке и технике. Одним из распространенных источников магнитного поля является соленоид - катушка с током. Чтобы эффективно использовать соленоид, нужно знать энергию его магнитного поля. В этой статье мы разберемся, что такое энергия магнитного поля соленоида, как ее вычислить и для чего она нужна.
1. Основы теории магнитного поля соленоида
Магнитное поле представляет собой особый вид физического поля, которое окружает движущиеся электрические заряды или постоянные магниты. Оно характеризуется определенной напряженностью и направлением в каждой точке пространства. Магнитное поле описывается с помощью вектора магнитной индукции.
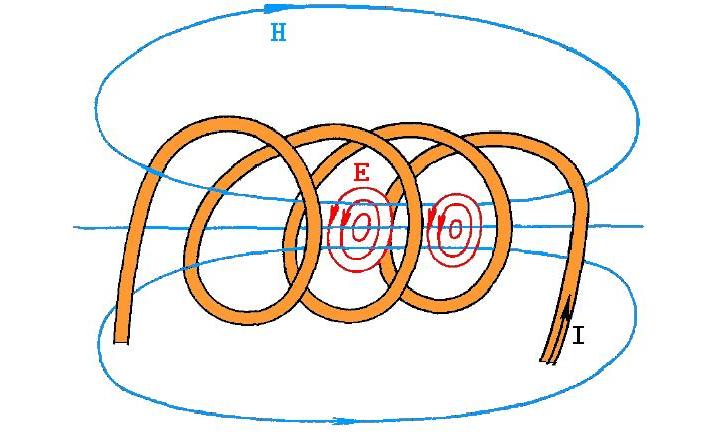
Соленоид представляет собой прямой длинный проводник, свернутый в виде спирали или катушки. При протекании по соленоиду электрического тока вокруг него образуется магнитное поле. Это поле имеет осевую симметрию и направлено по оси соленоида.
Основные характеристики магнитного поля соленоида:
- Магнитная индукция B - характеризует силу магнитного поля, измеряется в теслах (Тл).
- Напряженность магнитного поля H - характеризует напряженность магнитного поля, измеряется в амперах на метр (А/м).
- Эти величины связаны соотношением B = μH, где μ - магнитная проницаемость среды.
Сила магнитного поля соленоида зависит от:
- Силы тока в соленоиде - чем больше ток, тем сильнее поле.
- Количества витков - чем больше витков, тем сильнее поле.
- Радиуса соленоида - чем меньше радиус, тем сильнее поле.
- Материала сердечника - сердечник из ферромагнетика усиливает поле.
Таким образом, изменяя параметры соленоида, можно регулировать силу его магнитного поля.
2. Понятие энергии магнитного поля
Любое физическое поле, в том числе и магнитное, обладает определенной энергией. Энергию магнитного поля можно определить как количество работы, которое нужно затратить на создание этого поля.
Наличие энергии в магнитном поле можно продемонстрировать на примере катушки индуктивности. Если через катушку пропустить ток, то вокруг нее возникнет магнитное поле, содержащее некоторую энергию. При выключении тока эта энергия магнитного поля преобразуется в тепловую энергию.
Магнитная энергия и энергия электрического поля взаимосвязаны и описываются уравнениями Максвелла. Изменение магнитного поля порождает электрическое поле и наоборот.
Другим проявлением энергии магнитного поля является электромагнитная индукция - возникновение электрического тока в проводнике при его движении в магнитном поле. Этот ток обусловлен преобразованием энергии магнитного поля.
Таким образом, наличие энергии в магнитном поле экспериментально подтверждено и является важной характеристикой магнитного поля.
3. Выражение энергии через характеристики магнитного поля
Для выражения энергии магнитного поля через его характеристики используются следующие основные формулы:
- Энергия магнитного момента m во внешнем магнитном поле B:
W = -m·B - Энергия магнитного поля катушки индуктивности L при токе I:
W = (L·I2)/2 - Плотность энергии магнитного поля:
w = B·H / 2μ, где μ - магнитная проницаемость среды
При выводе этих формул используются некоторые допущения, например постоянство μ или линейность связи B и H. В реальных условиях эти допущения могут нарушаться, что вносит ограничения в применимость формул.
Тем не менее, эти выражения позволяют связать энергию магнитного поля с его важнейшими характеристиками и использовать эти формулы во многих практических приложениях.
Далее мы рассмотрим, как с помощью этих формул можно вычислить энергию магнитного поля реального объекта - соленоида.
4. Расчет энергии магнитного поля соленоида
Для расчета энергии магнитного поля конкретного соленоида необходимо знать следующие его параметры:
- Количество витков соленоида N
- Длина соленоида l
- Площадь поперечного сечения соленоида S
- Сила тока в соленоиде I
- Магнитная проницаемость материала сердечника μ
Для вычисления энергии используется формула:
W = (μ·N^2·S/l)·I^2 / 2
Рассмотрим пример расчета для соленоида с параметрами: N=100 витков, l=0.5 м, S=0.001 м^2, I=2 А, μ=μ0=4π·10−7 Гн/м.
Подставляя значения в формулу, получаем:
W = (4π·10^−7 ·100^2·0.001/0.5)·2^2 / 2 = 0.002 Дж
Для точности расчетов рекомендуется:
- Измерять размеры соленоида с минимальной погрешностью
- Использовать приборы с высоким классом точности для измерения тока
- Учитывать отклонение μ от μ0 для ферромагнетиков
5. Факторы, влияющие на энергию магнитного поля
На величину энергии магнитного поля соленоида влияют следующие основные факторы:
- Сила тока в соленоиде - энергия пропорциональна I^2
- Число витков соленоида - энергия пропорциональна N^2
- Размеры соленоида (длина и площадь сечения)
- Магнитная проницаемость среды и материала сердечника
Увеличивая эти параметры, можно наращивать энергию магнитного поля соленоида. Однако есть и ограничения - перегрев из-за высоких токов, насыщение магнитопроводящих материалов.

6. Применение расчета энергии магнитного поля
Знание энергии магнитного поля соленоида используется для:
- Оценки мощности источника питания соленоида
- Расчета параметров системы охлаждения
- Сравнения разных конструкций соленоидов
- Выбора оптимальных соотношений размеров соленоида
Например, если требуется соленоид с энергией поля 1 Дж, то по формуле можно подобрать оптимальное сочетание числа витков, размеров и силы тока.
Зная энергию, можно рассчитать мощность источника питания и тепловыделение в проводах для выбора системы охлаждения.
7. Экспериментальные методы определения энергии
Энергию магнитного поля соленоида можно определить экспериментально с помощью следующих методов:
- Измерение ЭДС самоиндукции при выключении тока в соленоиде
- Определение работы по перемещению магнита внутри соленоида
- Измерение нагрева проводника, движущегося в магнитном поле соленоида
Данные методы основаны на преобразовании энергии магнитного поля в другие виды энергии, что позволяет рассчитать ее исходное значение. Эксперимент дает возможность проверить и уточнить теоретические формулы для конкретных условий.
8. Примеры использования энергии магнитного поля соленоида
Энергия магнитного поля соленоидов широко применяется в различных областях:
- Электромагниты - за счет энергии магнитного поля создается механическая сила притяжения/отталкивания
- Электродвигатели - энергия магнитного поля преобразуется в механическую энергию вращения ротора
- Магнитная левитация - использование отталкивания магнитным полем для подвешивания объектов без контакта
Важный класс применений - ускорители заряженных частиц. Например, в циклотроне заряженные частицы разгоняются за счет энергии магнитного поля.
9. Сверхпроводящие соленоиды
Особого внимания заслуживают сверхпроводящие соленоиды. Используя сверхпроводники с нулевым сопротивлением, можно создавать очень сильные магнитные поля при относительно небольших размерах.
Сверхпроводящие соленоиды позволяют накапливать энергию магнитного поля в 10-100 раз больше, чем обычные.
Это открывает перспективы создания компактных накопителей энергии, источников постоянного тока высокой мощности.
10. Бесконтактная передача энергии
Активно исследуется возможность беспроводной передачи электроэнергии с помощью магнитного поля на расстояние.
Для этого используются соленоиды передатчика и приемника, резонансно настроенные друг на друга. Энергия передается посредством электромагнитных волн.
Такая технология может найти применение для зарядки мобильных устройств, питания имплантируемых медицинских приборов.
11. Перспективные разработки
Ведутся работы по созданию магнитных двигателей, использующих отталкивание магнитных полей без контакта подвижных частей.
Перспективно применение сильных импульсных магнитных полей в медицине, например в магнитной терапии опухолей.
Разрабатываются методы бесконтактного управления химическими реакциями с помощью локальных магнитных полей.
Все это требует глубокого понимания поведения и возможностей магнитного поля соленоидов.


























