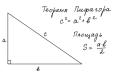
Гипотенуза - это сторона прямоугольного треугольника, лежащая напротив прямого угла. Она является самой длинной стороной и играет важнейшую роль в формулах и теоремах, связанных с прямоугольным треугольником. Изучение гипотенузы восходит еще к древнегреческим математикам, в частности к Пифагору, который открыл знаменитую теорему о соотношении сторон прямоугольного треугольника.
В данной статье мы подробно рассмотрим, что представляет собой гипотенуза, какие свойства она имеет и как ее можно вычислить, зная другие элементы треугольника. Также приведем примеры практического применения формул для нахождения гипотенузы при решении задач.
Определение гипотенузы треугольника
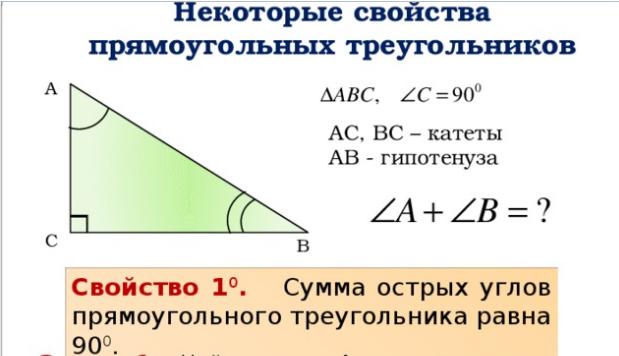
Гипотенуза - это наибольшая сторона в прямоугольном треугольнике, лежащая напротив прямого угла. Остальные две стороны называются катетами. Гипотенуза всегда длиннее любого из катетов.
Длину гипотенузы можно найти несколькими способами. Самый известный - это использовать теорему Пифагора: квадрат гипотенузы равен сумме квадратов катетов. То есть, зная длины катетов, можно вычислить гипотенузу.
Также для нахождения гипотенузы используют тригонометрические соотношения. Если известен один из острых углов и противолежащий катет, можно найти гипотенузу по теореме косинусов. А если дан угол и прилежащий катет - по теореме синусов.
Формулы для вычисления гипотенузы
Существует несколько основных формул, позволяющих найти длину гипотенузы треугольника в зависимости от известных данных:
- Теорема Пифагора (при известных катетах a и b): c = √(a2 + b2), где c - гипотенуза
- Теорема косинусов (при известном угле α и прилежащем катете a): c = a / cos(α)
- Теорема синусов (при известном угле α и противолежащем катете b): c = b / sin(α)
Кроме того, существуют формулы для некоторых частных случаев:
- Для равнобедренного прямоугольного треугольника с известным катетом a: c = √2 * a
- Если угол при вершине равен 30°, а противолежащий катет b: c = 2 * b
- Если угол при вершине равен 45°, а противолежащий катет b: c = b * √2
Помимо этого, гипотенузу можно найти, используя свойства высоты, медианы, биссектрисы или радиусов вписанной и описанной окружностей в прямоугольном треугольнике.
Применение свойств гипотенузы на практике
Знание свойств гипотенузы и умение находить ее длину используется для решения множества практических задач.
В строительстве при возведении различных конструкций и сооружений часто приходится иметь дело с треугольниками. Например, для расчета несущей способности крыши или опоры может потребоваться найти длину гипотенузы треугольника, образованного элементами конструкции.
В навигации и геодезии при построении топографических карт, расчете расстояний также применяются формулы для нахождения гипотенузы треугольника.
В физике свойства прямоугольного треугольника используются для вывода формул, связывающих скорость, ускорение и перемещение при равноускоренном движении.
В программировании для определения расстояния между двумя точками на плоскости часто используют теорему Пифагора.
Для расчета площадей различных фигур, имеющих форму треугольника, также применяют формулы, связывающие стороны прямоугольного треугольника.
В логистике при планировании маршрутов доставки грузов необходимо вычислять расстояния между пунктами, для чего также используют соотношения в прямоугольном треугольнике.

Резюме по теме гипотенуза треугольника
Итак, давайте подведем итоги по теме гипотенуза треугольника.
Гипотенуза - это наибольшая сторона только в прямоугольном треугольнике. Она располагается напротив прямого угла. Две другие стороны прямоугольного треугольника называются катетами.
Существует несколько основных способов вычисления длины гипотенузы:
- - Теорема Пифагора - если известны длины обоих катетов;
- - Теорема косинусов - если дан острый угол и прилежащий катет;
- - Теорема синусов - если известен острый угол и противолежащий катет.
Кроме того, существуют частные формулы для некоторых специальных случаев, например, когда угол равен 30 или 45 градусам.
Знание свойств гипотенузы прямоугольного треугольника позволяет решать множество практических задач в самых разных областях - от строительства до программирования.
Таким образом, умение находить гипотенузу по известным элементам треугольника - важный навык, которым должен владеть каждый, кто занимается точными науками и инженерией.