Биссектриса - простая линия в геометрии, делящая угол пополам. Казалось бы, что в этом такого важного? Оказывается, это фундаментальное свойство позволяет строить окружности внутри треугольников, находить центры отрезков, делить фигуры на равные части.
Понимание свойств биссектрисы важно при изучении геометрии в школе и для решения многих практических задач. В этой статье мы рассмотрим, почему так важно, что биссектриса всегда делит угол пополам.
Как биссектриса помогает строить окружности в треугольниках
Биссектриса угла треугольника обладает важным свойством - она делит противоположную сторону на отрезки, пропорциональные прилежащим к этому углу сторонам. Это позволяет использовать биссектрисы для построения окружностей, вписанных в треугольник.
Известно, что все три биссектрисы треугольника пересекаются в одной точке, являющейся центром окружности, вписанной в этот треугольник. То есть для построения вписанной окружности достаточно провести биссектрисы ко всем трем углам треугольника и найти точку их пересечения.
Помимо этого, зная длины сторон треугольника и воспользовавшись свойством биссектрисы, можно найти радиус вписанной окружности. Для этого достаточно выразить длину одной из биссектрис через стороны треугольника и подставить известные значения.
Также с помощью биссектрис можно построить окружность, описанную около треугольника. В этом случае достаточно продолжить все три биссектрисы треугольника до пересечения с продолжениями сторон и соединить полученные точки окружностью.
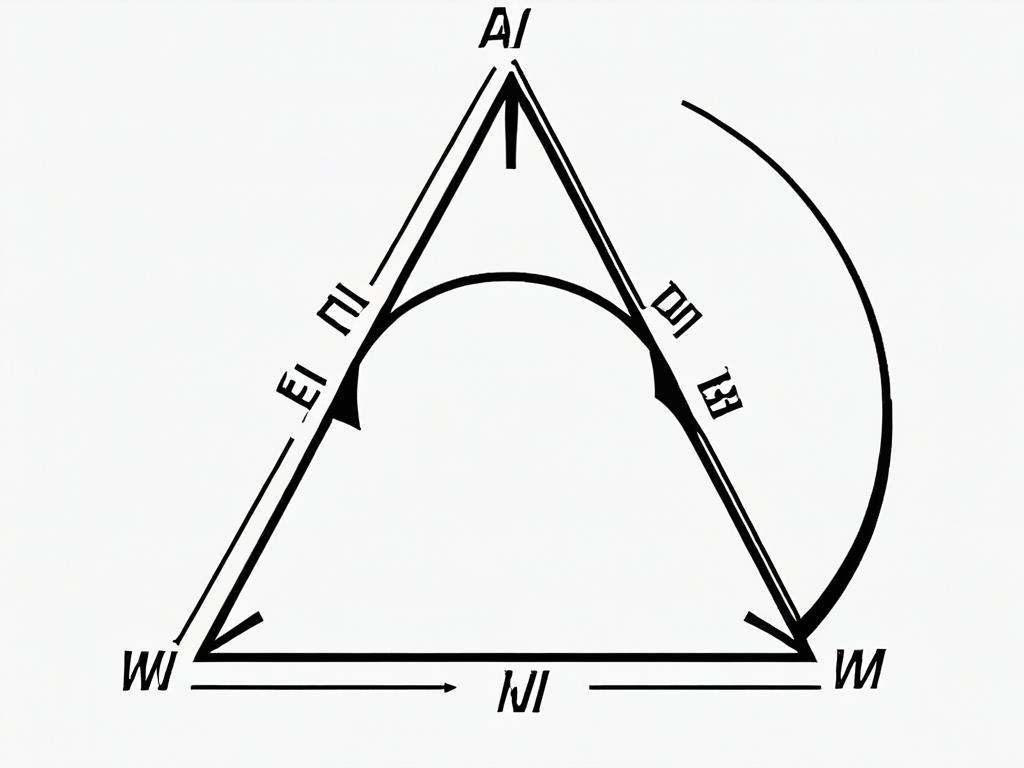
Свойство биссектрисы для деления отрезков пополам
Одним из важнейших свойств биссектрисы является ее способность делить данный ей угол пополам. Это свойство вытекает из самого определения биссектрисы и является ее отличительной особенностью.
Рассмотрим это свойство более подробно. Пусть дан некоторый угол ABC. Если провести в нем биссектрису AD, то она разделит угол на два равных угла ABD и ACD. Это следует из равенства расстояний от любой точки биссектрисы AD до сторон угла AB и AC. Так как эти расстояния равны для любой точки биссектрисы, углы ABD и ACD, образованные биссектрисой, будут равны.
То есть фактически биссектриса выполняет «разрезание» угла пополам, откуда и происходит само название этой линии. При этом получаемые углы ABD и ACD являются как бы «половинками» от исходного угла ABC, что и дало повод говорить о делении угла биссектрисой надвое или пополам.
Это универсальное свойство биссектрисы применимо не только к углам в треугольниках, но и к любым углам, в том числе и к развернутым. Например, если взять развернутый угол и провести в нем биссектрису, эта прямая разделит его на два равных угла в 180 градусов.
Кроме того, с помощью биссектрисы можно делить пополам не только углы, но и отрезки. Для этого достаточно построить угол с вершиной в одном из концов отрезка и сторонами, проходящими через другой конец отрезка. Если в этом угле провести биссектрису, она пересечет исходный отрезок в точке, делящей его пополам.
Такое применение биссектрисы позволяет быстро и просто находить середину отрезков, не прибегая к измерению длин. Это особенно удобно при решении различных геометрических задач, требующих деления заданных отрезков на равные части.
Применение биссектрисы в решении геометрических задач
Рассмотренные выше свойства биссектрисы, в частности, ее способность делить углы и отрезки точно пополам, делают это понятие чрезвычайно полезным при решении разнообразных геометрических задач.
К примеру, для нахождения центра окружности, вписанной в треугольник или описанной около него, зачастую используют именно построение биссектрис. Их пересечение и будет искомой точкой.
При вычислении неизвестных элементов треугольника тоже нередко применяют формулы, содержащие длины биссектрис. Подставляя в них известные величины, можно найти нужный параметр.
Еще одно распространенное применение биссектрис - это деление отрезков на равные части при решении конструктивных заданий. С помощью биссектрисы легко разбить отрезок пополам, а затем и на большее число равных интервалов.
В целом, умелое использование свойств биссектрисы позволяет существенно упростить решение многих геометрических задач, связанных с нахождением центров окружностей, вычислением неизвестных величин в треугольниках и построением отрезков. Поэтому знание этих свойств и владение навыками применения биссектрис является важной составляющей геометрической подготовки.
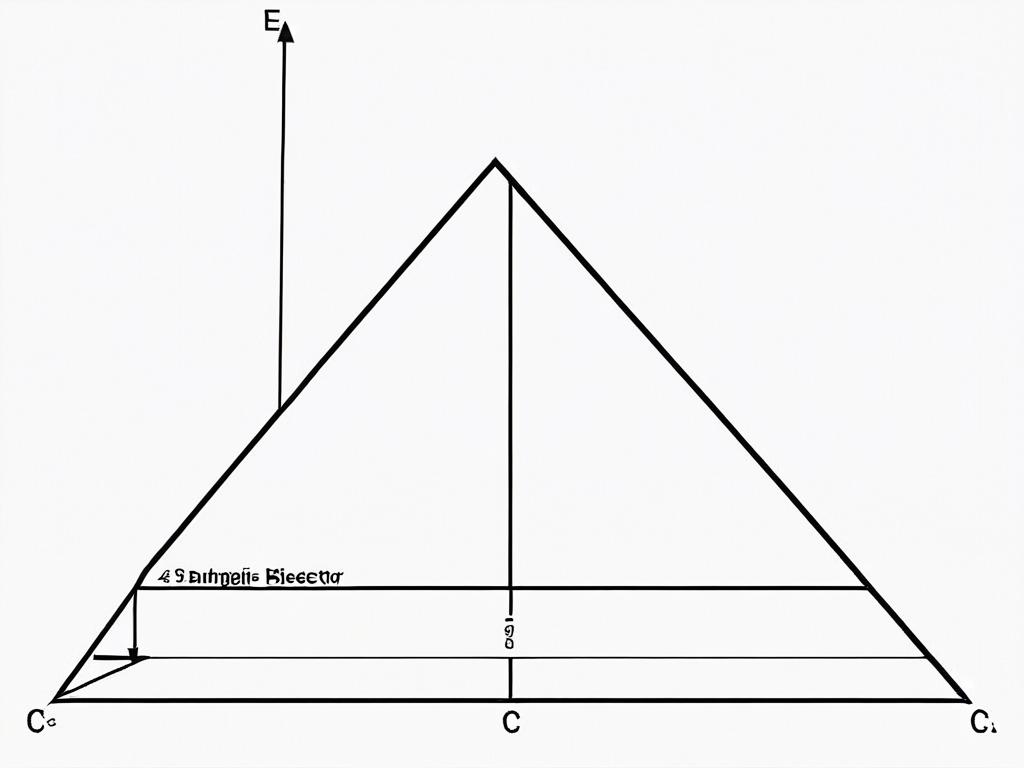
Выводы о важности свойства биссектрисы
Рассмотрев основные свойства биссектрисы, в частности, ее способность делить углы и отрезки строго пополам, можно сделать вывод о большой важности этого инструмента в геометрии.
Во-первых, благодаря точному делению углов и отрезков, биссектриса позволяет находить центры окружностей, описанных около фигур и вписанных в них. А это ключевой момент при решении многих задач.
Во-вторых, свойства биссектрисы активно применяются при вычислении неизвестных параметров в треугольниках и других фигурах. Зная значения одних элементов, по формулам, содержащим биссектрисы, находят нужные величины.
В-третьих, биссектриса широко используется в различных геометрических построениях, если требуется разбить отрезки или лучи на равные интервалы. Это сильно упрощает выполнение конструктивных заданий.
Таким образом, универсальность биссектрисы, ее простота и надежность делают это понятие поистине незаменимым инструментом геометрии. И владение методами применения биссектрис является обязательным для каждого, кто занимается данной наукой.

























